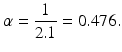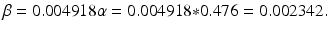(1)
Department of Mathematics, University of Florida, Gainesville, FL, USA
2.1 Kermack–McKendrick SIR Epidemic Model
Introduction to epidemic modeling is usually made through one of the first epidemic models proposed by Kermack and McKendrick in 1927, a model known as the SIR epidemic model [84].
2.1.1 Deriving the Kermack–McKendrick Epidemic Model
When a disease spreads in a population, it splits the population into nonintersecting classes. In one of the simplest scenarios, there are three such classes:
The class of individuals who are healthy but can contract the disease. These are called susceptible individuals or susceptibles. The size of this class is usually denoted by S.
The class of individuals who have contracted the disease and are now sick with it, called infected individuals. In this model, it is assumed that infected individuals are also infectious (see Chap. 1 for distinction between infected and infectious individuals). The size of the class of infectious/infected individuals is denoted by I.
The class of individuals who have recovered and cannot contract the disease again are called removed/recovered individuals. The class of recovered individuals is usually denoted by R.
The number of individuals in each of these classes changes with time, that is, S(t), I(t), and R(t) are functions of time t. The total population size N is the sum of the sizes of these three classes:
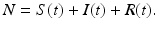 To formulate a model, we have to make assumptions to simplify reality. The first assumption for the Kermack–McKendrick model is that infected individuals are also infectious. The second assumption of the model is that the total population size remains constant.
To formulate a model, we have to make assumptions to simplify reality. The first assumption for the Kermack–McKendrick model is that infected individuals are also infectious. The second assumption of the model is that the total population size remains constant.
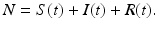
Epidemiological models consist of systems of ODEs that describe the dynamics in each class. One of the simplest models involves the dynamics of susceptible, infectious, and recovered individuals. The model was first proposed by Kermack and McKendrick in 1927 [84].
To derive the differential equations, we consider how the classes change over time. When a susceptible individual enters into contact with an infectious individual, that susceptible individual becomes infected with a certain probability and moves from the susceptible class into the infected class. The susceptible population decreases in a unit of time by all individuals who become infected in that time. At the same time, the class of infectives increases by the same number of newly infected individuals. The number of individuals who become infected per unit of time in epidemiology is called incidence, and the rate of change of the susceptible class is given by
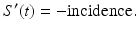 How can we represent the incidence? Consider one infectious individual. Assume:
How can we represent the incidence? Consider one infectious individual. Assume:
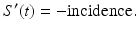
cN is the number of contacts per unit of time this infectious individual makes. Here we assume that the number of contacts made by one infectious individual is proportional to the total population size with per capita contact rate c.
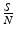 is the probability that a contact is with a susceptible individual. Thus,
is the probability that a contact is with a susceptible individual. Thus,
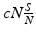 is number of contacts with susceptible individuals that one infectious individual makes per unit of time. Not every contact with a susceptible individual necessarily leads to transmission of the disease. Suppose p is the probability that a contact with a susceptible individual results in transmission. Then,
is number of contacts with susceptible individuals that one infectious individual makes per unit of time. Not every contact with a susceptible individual necessarily leads to transmission of the disease. Suppose p is the probability that a contact with a susceptible individual results in transmission. Then,
pcS is number of susceptible individuals who become infected per unit of time per infectious individual.
β S I is the number of individuals who become infected per unit of time (incidence). Here we have set β = pc.
If we define 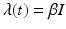 , then the number of individuals who become infected per unit of time is equal to
, then the number of individuals who become infected per unit of time is equal to 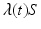 . The function
. The function 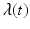 is called the force of infection. The coefficient β is the constant of proportionality called the transmission rate constant. The number of infected individuals in the population I(t) is called the prevalence of the disease.
is called the force of infection. The coefficient β is the constant of proportionality called the transmission rate constant. The number of infected individuals in the population I(t) is called the prevalence of the disease.
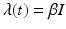 , then the number of individuals who become infected per unit of time is equal to
, then the number of individuals who become infected per unit of time is equal to 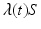 . The function
. The function 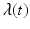 is called the force of infection. The coefficient β is the constant of proportionality called the transmission rate constant. The number of infected individuals in the population I(t) is called the prevalence of the disease.
is called the force of infection. The coefficient β is the constant of proportionality called the transmission rate constant. The number of infected individuals in the population I(t) is called the prevalence of the disease.There are different types of incidence depending on the assumption made about the form of the force of infection. One form is called mass action incidence. With this form of incidence, we obtain the following differential equation for susceptible individuals:
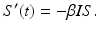 The susceptible individuals who become infected move to the class I. Those individuals who recover or die leave the infected class at constant per capita probability per unit of time α, called the recovery rate. That is, α I is the number of infected individuals per unit of time who recover. So,
The susceptible individuals who become infected move to the class I. Those individuals who recover or die leave the infected class at constant per capita probability per unit of time α, called the recovery rate. That is, α I is the number of infected individuals per unit of time who recover. So,
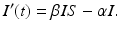 Individuals who recover leave the infectious class and move to the recovered class
Individuals who recover leave the infectious class and move to the recovered class
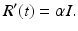 Thus, the whole model is given by the following system of ODEs:
Thus, the whole model is given by the following system of ODEs:
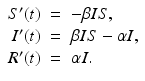
To be well defined mathematically, this system is equipped with given initial conditions S(0), I(0), and R(0).
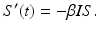
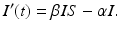
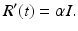
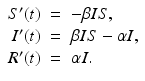
(2.1)
When we formulate a model, we need to be concerned with the units of the quantities involved. Units are also helpful when we estimate parameters from data. The units of both sides of the above equations must be the same. All derivatives have units number of people per unit of time (why?). Hence, each term on the right-hand side should have the same units. From the first equation, we see that since I and S have units number of people, the units of β must be 1/[number of people×unit of time]. Since β = pc and p is a probability, which has no units, the units of c must be 1/[number of people×unit of time]. Thus the contact rate cN has units 1/unit of time. Similarly, from the second equation, we see that the units of α are 1/unit of time, so the term α I has units number of people/unit of time.
Loosely speaking, a differential equation model such as the model (2.1) is well posed if through every point (initial condition), there exists a unique solution. Differential equation models must be well posed to be mathematically acceptable and biologically significant. Because the dependent variables in the model denote physical quantities, for most models in biology and epidemiology, we also require that solutions that start from positive (nonnegative) initial conditions remain positive (nonnegative) for all time.
We denote by N the total population size at time zero 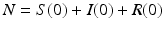 . Adding all three equations in system (2.1), we obtain
. Adding all three equations in system (2.1), we obtain 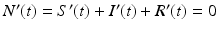 . Hence, N(t) is constant and equal to its initial value, N(t) = N. This model is called the SIR model or SIR system. It is a special type of model called a compartmental model, because each letter refers to a “compartment” in which an individual can reside. Each individual can reside in exactly one compartment and can move from one compartment to another. Compartmental models are schematically described by a diagram often called a flowchart. Each compartment in a flowchart is represented by a box indexed by the name of the class. Arrows indicate the direction of movement of individuals between the classes. The movement arrows are typically labeled by the transition rates (see Fig. 2.1).
. Hence, N(t) is constant and equal to its initial value, N(t) = N. This model is called the SIR model or SIR system. It is a special type of model called a compartmental model, because each letter refers to a “compartment” in which an individual can reside. Each individual can reside in exactly one compartment and can move from one compartment to another. Compartmental models are schematically described by a diagram often called a flowchart. Each compartment in a flowchart is represented by a box indexed by the name of the class. Arrows indicate the direction of movement of individuals between the classes. The movement arrows are typically labeled by the transition rates (see Fig. 2.1).

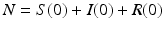 . Adding all three equations in system (2.1), we obtain
. Adding all three equations in system (2.1), we obtain 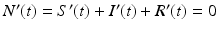 . Hence, N(t) is constant and equal to its initial value, N(t) = N. This model is called the SIR model or SIR system. It is a special type of model called a compartmental model, because each letter refers to a “compartment” in which an individual can reside. Each individual can reside in exactly one compartment and can move from one compartment to another. Compartmental models are schematically described by a diagram often called a flowchart. Each compartment in a flowchart is represented by a box indexed by the name of the class. Arrows indicate the direction of movement of individuals between the classes. The movement arrows are typically labeled by the transition rates (see Fig. 2.1).
. Hence, N(t) is constant and equal to its initial value, N(t) = N. This model is called the SIR model or SIR system. It is a special type of model called a compartmental model, because each letter refers to a “compartment” in which an individual can reside. Each individual can reside in exactly one compartment and can move from one compartment to another. Compartmental models are schematically described by a diagram often called a flowchart. Each compartment in a flowchart is represented by a box indexed by the name of the class. Arrows indicate the direction of movement of individuals between the classes. The movement arrows are typically labeled by the transition rates (see Fig. 2.1).
Fig. 2.1
Flowchart of the Kermack–McKendrick SIR epidemic model
2.1.2 Mathematical Properties of the SIR Model
The Kermack–McKendrick epidemic model (2.1) has very distinctive dynamics. Because S′ < 0 for all t, the number of susceptible individuals is always declining, independently of the initial condition S(0). Since S(t) is monotone and positive, we have
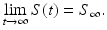 The number of recovered individuals also has monotone behavior, independently of the initial conditions. Since R′ > 0 for all t, the number of recovered individuals is always increasing. Since the number of recovered is monotone and bounded by N, we have
The number of recovered individuals also has monotone behavior, independently of the initial conditions. Since R′ > 0 for all t, the number of recovered individuals is always increasing. Since the number of recovered is monotone and bounded by N, we have
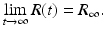 On the other hand, the number of infected individuals may be monotonically decreasing to zero, or may have nonmonotone behavior by first increasing to some maximum level, and then decreasing to zero (see Fig. 2.2). The prevalence first starts increasing if
On the other hand, the number of infected individuals may be monotonically decreasing to zero, or may have nonmonotone behavior by first increasing to some maximum level, and then decreasing to zero (see Fig. 2.2). The prevalence first starts increasing if ![$$I'(0) = (\beta S(0)-\alpha )I(0) > 0$$
” src=”/wp-content/uploads/2016/11/A304573_1_En_2_Chapter_IEq8.gif”></SPAN>. Hence, a necessary and sufficient condition for an initial increase in the number of infecteds is <SPAN class=EmphasisTypeItalic>β S</SPAN>(0) −<SPAN class=EmphasisTypeItalic>α</SPAN> > 0, or<br />
<DIV id=Equh class=Equation><br />
<DIV class=EquationContent><br />
<DIV class=MediaObject><IMG alt=]() 1.}$$
” src=”/wp-content/uploads/2016/11/A304573_1_En_2_Chapter_Equh.gif”>
1.}$$
” src=”/wp-content/uploads/2016/11/A304573_1_En_2_Chapter_Equh.gif”>
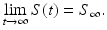
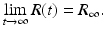
Fig. 2.2
Left: shows the prevalence monotonically decreasing. Right: shows the prevalence first increasing and then decreasing to zero
This sudden increase in the prevalence and then a decline to zero is a classical model of an epidemic or outbreak. Threshold conditions for an epidemic to occur are common in epidemiology, and we will discuss them in detail later on. To determine the limits 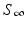 and
and 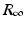 , we divide the equation for S and the equation for R. Hence,
, we divide the equation for S and the equation for R. Hence,
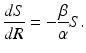 Solving, we have
Solving, we have
![$$\displaystyle{S = S(0)e^{-\frac{\beta }{\alpha }R} \geq S(0)e^{-\frac{\beta }{\alpha }N} > 0.}$$
” src=”/wp-content/uploads/2016/11/A304573_1_En_2_Chapter_Equj.gif”></DIV></DIV></DIV>We conclude that <SPAN id=IEq11 class=InlineEquation><IMG alt=]() 0$$
” src=”/wp-content/uploads/2016/11/A304573_1_En_2_Chapter_IEq11.gif”>. The quantity
0$$
” src=”/wp-content/uploads/2016/11/A304573_1_En_2_Chapter_IEq11.gif”>. The quantity 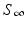 is called the final size of the epidemic. We see that the epidemic does not end, because all susceptible individuals have been infected and are now immune. Some individuals always escape a disease—an observation that was made in practice is also confirmed by the SIR model.
is called the final size of the epidemic. We see that the epidemic does not end, because all susceptible individuals have been infected and are now immune. Some individuals always escape a disease—an observation that was made in practice is also confirmed by the SIR model.
Get Clinical Tree app for offline access

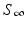 and
and 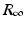 , we divide the equation for S and the equation for R. Hence,
, we divide the equation for S and the equation for R. Hence,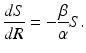
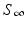 is called the final size of the epidemic. We see that the epidemic does not end, because all susceptible individuals have been infected and are now immune. Some individuals always escape a disease—an observation that was made in practice is also confirmed by the SIR model.
is called the final size of the epidemic. We see that the epidemic does not end, because all susceptible individuals have been infected and are now immune. Some individuals always escape a disease—an observation that was made in practice is also confirmed by the SIR model.Finally, we show that the epidemic dies out. If
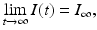 then
then 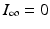 . This is evident from the plots in Fig. 2.2, but a mathematical argument can establish the result for all parameters. To see this, we integrate the first equation in (2.1):
. This is evident from the plots in Fig. 2.2, but a mathematical argument can establish the result for all parameters. To see this, we integrate the first equation in (2.1):
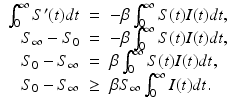
The last inequality implies that I(t) is integrable on 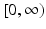 . Hence,
. Hence, 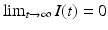 .
.
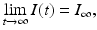
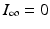 . This is evident from the plots in Fig. 2.2, but a mathematical argument can establish the result for all parameters. To see this, we integrate the first equation in (2.1):
. This is evident from the plots in Fig. 2.2, but a mathematical argument can establish the result for all parameters. To see this, we integrate the first equation in (2.1):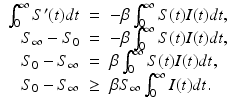
(2.2)
 . Hence,
. Hence, 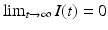 .
.The Kermack–McKendrick model is based on several assumptions: (1) There are no births and deaths in the population. (2) The population is closed, that is, no one from the outside enters the population, and no one leaves the population, and finally, (3) All recovered individuals have complete immunity and cannot be infected again. These assumptions seem very restrictive, but within limits, they can be satisfied. We will see a specific example in Sect. 2.3. Diseases that lead to permanent immunity and are well modeled by the SIR epidemic model are most diseases typical of childhood years, often called childhood diseases. These include chickenpox, smallpox, rubella, and mumps.
To solve the system, we first notice that the variable R does not participate in the first two equations. Thus we can consider only the equations for S and I, which are coupled, and leave out the equation for R. The variable R can then be obtained in this model from the relation 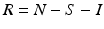 :
:
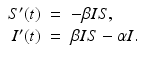
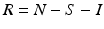 :
: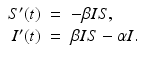
(2.3)
Dividing the two equations, we obtain
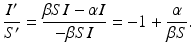 Separating the variables, we have
Separating the variables, we have
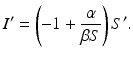 Integrating leads to
Integrating leads to
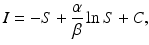 where C is an arbitrary constant. Thus, the orbits of the solution are given implicitly by the equation
where C is an arbitrary constant. Thus, the orbits of the solution are given implicitly by the equation
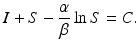
The Kermack–McKendrick model is equipped with initial conditions: S 0 = S(0) and I 0 = I(0). Those are given. We also have that 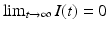 , while
, while 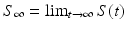 gives the final number of susceptible individuals after the epidemic is over. The above equality holds both for (S 0, I 0) and for
gives the final number of susceptible individuals after the epidemic is over. The above equality holds both for (S 0, I 0) and for 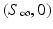 . Thus,
. Thus,
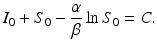 Consequently,
Consequently,
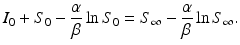 Rearranging terms, we get
Rearranging terms, we get
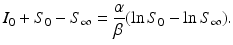 Therefore,
Therefore,
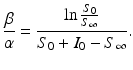
We note that since S(t) is a decreasing function, we have 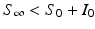 . The implicit solution also allows us to compute the maximum number of infected individuals that is attained. This number occurs when I′ = 0, that is, when
. The implicit solution also allows us to compute the maximum number of infected individuals that is attained. This number occurs when I′ = 0, that is, when
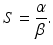
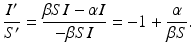
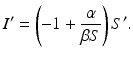
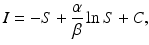
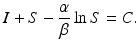
(2.4)
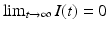 , while
, while 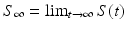 gives the final number of susceptible individuals after the epidemic is over. The above equality holds both for (S 0, I 0) and for
gives the final number of susceptible individuals after the epidemic is over. The above equality holds both for (S 0, I 0) and for 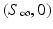 . Thus,
. Thus,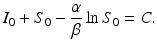
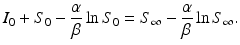
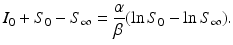
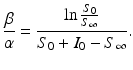
(2.5)
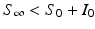 . The implicit solution also allows us to compute the maximum number of infected individuals that is attained. This number occurs when I′ = 0, that is, when
. The implicit solution also allows us to compute the maximum number of infected individuals that is attained. This number occurs when I′ = 0, that is, when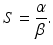
From
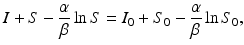 substituting the expression for S and moving all terms but I to the right-hand side leads to
substituting the expression for S and moving all terms but I to the right-hand side leads to
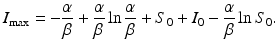
Here 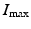 is the maximum number of infected individuals reached in the epidemic. It signifies the maximum severity of the epidemic. If we are able to estimate
is the maximum number of infected individuals reached in the epidemic. It signifies the maximum severity of the epidemic. If we are able to estimate 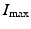 for a newly occurring infectious disease, we will know when the number of infections will begin to decline.
for a newly occurring infectious disease, we will know when the number of infections will begin to decline.
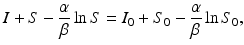
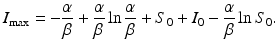
(2.6)
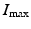 is the maximum number of infected individuals reached in the epidemic. It signifies the maximum severity of the epidemic. If we are able to estimate
is the maximum number of infected individuals reached in the epidemic. It signifies the maximum severity of the epidemic. If we are able to estimate 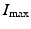 for a newly occurring infectious disease, we will know when the number of infections will begin to decline.
for a newly occurring infectious disease, we will know when the number of infections will begin to decline.2.2 The Kermack–McKendrick Model: Estimating Parameters from Data
When we are given specific disease and time series data for it, we can estimate the parameters of the SIR model and compare the solution of the model with the data. This section follows the description in [27]. See [27] for a different example.
2.2.1 Estimating the Recovery Rate
For many diseases, information about the mean duration of the exposed period or the infectious period can easily be obtained. For instance, for influenza, the duration of the infectious period is 3–7 days with mean 4–5 days. How can that help us estimate the recovery rate α? To approach that question, let us assume that there is no inflow in the infectious class and a certain number of individuals I 0 have been put in the infectious class at time zero. Then the differential equation that gives the dynamics of this class is given by
 This equation can be easily solved. Therefore, the number of people in the infectious class at time t is given by
This equation can be easily solved. Therefore, the number of people in the infectious class at time t is given by
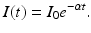 Consequently,
Consequently,
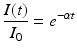

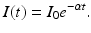
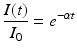
for t ≥ 0 gives the proportion of people who are still infectious at time t, or in probability language, it gives the probability of being still infectious at time t. We can compute the fraction of individuals who have left the infectious class,
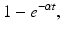 or in probability terms,
or in probability terms,
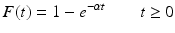 is the probability of recovering/leaving the infectious class in the interval [0, t). Clearly, F(t) is a probability distribution (if defined as zero for t < 0). The probability density function is
is the probability of recovering/leaving the infectious class in the interval [0, t). Clearly, F(t) is a probability distribution (if defined as zero for t < 0). The probability density function is 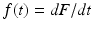 . Consequently,
. Consequently,
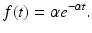 Note: f(t) = 0 for t < 0. Furthermore, the average time spent in the infectious class is given by the mean (expected value of a random variable X, denoting time to exiting the infectious class),
Note: f(t) = 0 for t < 0. Furthermore, the average time spent in the infectious class is given by the mean (expected value of a random variable X, denoting time to exiting the infectious class),
![$$\displaystyle{E[X] =\int _{ -\infty }^{\infty }tf(t)dt.}$$](/wp-content/uploads/2016/11/A304573_1_En_2_Chapter_Equz.gif) Therefore, computing that integral yields
Therefore, computing that integral yields
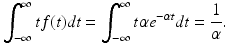 Thus we conclude that
Thus we conclude that
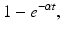
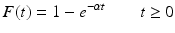
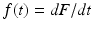 . Consequently,
. Consequently,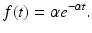
![$$\displaystyle{E[X] =\int _{ -\infty }^{\infty }tf(t)dt.}$$](/wp-content/uploads/2016/11/A304573_1_En_2_Chapter_Equz.gif)
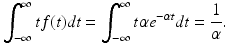
mean time spent in the infectious class = 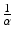 .
.
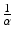 .
.For influenza, we are sick with it for 3–7 days. Say that the mean time spent as infectious is 5 days. Thus the recovery rate, measured in units of [days]−1, is 1/5.
Estimating the transmission rate β is quite a bit more difficult. Estimating β is possible for the Kermack–McKendrick model, because that model is relatively simple. In particular, we can obtain an implicit solution. An implicit solution is rarely obtainable for epidemic models, and estimating parameters for epidemic models requires techniques different from the one presented below. We will discuss these techniques in Chap. 6
2.2.2 The SIR Model and Influenza at an English Boarding School 1978
In January and February 1978, an epidemic of influenza occurred in a boarding school in the north of England. The boarding school housed a total of 763 boys, all of whom were at risk during the epidemic. The spring term began on January 10. The boys returned from their Christmas vacation spent at many different locations in the world. A boy returning from Hong Kong exhibited elevated temperature during the period 15–18 January. On January 22, three boys were sick. Table 2.1 gives the number of boys ill on the nth day beginning January 22 (n = 1).
Table 2.1
Daily number of influenza-infected boys
Day | No. infecteda | Day | No. infected |
|---|---|---|---|
3 | 25 | 9 | 192 |
4 | 75 | 10 | 126 |
5 | 227 | 11 | 71 |
6 | 296 | 12 | 28 |
7 | 258 | 13 | 11 |
8 | 236 | 14 | 7 |
The number of boys who escaped influenza was 19. The average time spent sick was 5–6 days. However, since boys were isolated in the infirmary, they spent perhaps about 2 days as infectious. A swab taken from some of the boys revealed that they were infected with H1N1 influenza A virus. The staff of the boarding school remained healthy, with only one staff member displaying symptoms of illness.
These data give the following values: S 3 = 738, I 3 = 25,  .
.
 .
.From the computations above, we have
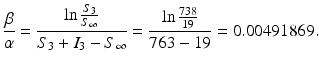
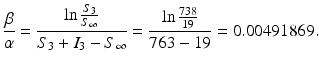
(2.7)
We measure time in days. We take t 0 = 0 to be January 21. The first datum is given on January 22, which gives t = 1. We have that t end = 14 is the February 4, 1978.
We take the infective period to be 2.1 days. This value can be obtained as the best fit as values around 2 days are tried with the procedure below. After we fix the duration of the infectious period, we compute α as the reciprocal of the time spent as an infectious individual (infectious period):
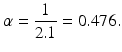 From Eq. (2.7) and using the value for α, we can obtain the value for β:
From Eq. (2.7) and using the value for α, we can obtain the value for β: