Chapter 1
Introduction
At the start of each chapter, we will ‘set the scene’ by outlining its content. In this introductory chapter, we start Section 1.1 by describing some situations where a mixed models analysis will be particularly helpful. In Section 1.2, we describe a simplified example and use it to illustrate the idea of a statistical model. We then introduce and compare fixed effects and random effects models. In the next section, we consider a more complex ‘real-life’ multi-centre trial and look at some of the variety of models that could be fitted (Section 1.3). This example will be used for several illustrative examples throughout the book. In Section 1.4, the use of mixed models to analyse a series of observations (repeated measures) is considered. Section 1.5 broadens the discussion on mixed models and looks at mixed models with a historical perspective of their use. In Section 1.6, we introduce some technical concepts: containment, balance and error strata.
We will assume in our presentation that the reader is already familiar with some of the basic statistical concepts as found in elementary statistical textbooks.
1.1 The use of mixed models
In the course of this book, we will encounter many situations in which a mixed models approach has advantages over the conventional type of analysis, which would be accessible via introductory texts on statistical analysis. Some of them are introduced in outline in this chapter and will be dealt in detail later on.
- Example 1: Utilisation of incomplete information in a cross-over trial Cross-over trials are often utilised to assess treatment efficacy in chronic conditions, such as asthma. In such conditions, an individual patient can be tested for response to a succession of two or more treatments, giving the benefit of a ‘within-patient’ comparison. In the most commonly used cross-over design, just two treatments are compared. If, for generality, we call these treatments A and B, then patients will be assessed either on their response to treatment A, followed by their response to treatment B, or vice versa. If all patients complete the trial, and both treatments are assessed, then the analysis is fairly straightforward. However, commonly, patients drop out during the trial and may have a valid observation from only the first treatment period. These incomplete observations cannot be utilised in a conventional analysis. In contrast, the use of a mixed model will allow all of the observations to be analysed, resulting in more accurate comparisons of the efficacy of treatment. This benefit, of more efficient use of the data, applies to all types of cross-over trial where there are missing data.
- Example 2: Cross-over trials with fewer treatment periods than treatments In cross-over trials, for logistical reasons, it may be impractical to ask a patient to evaluate more than two treatments (e.g. if the treatment has to be given for several weeks). Nevertheless, there may be the need to evaluate three or more treatments. Special types of cross-over design can be used in this situation, but a simple analysis will be very inefficient. Mixed models provide a straightforward method of analysis, which fully uses the data, resulting again in more precise estimates of the effect of the treatments.
- Example 3: A surgical audit A surgical audit is to be carried out to investigate how different hospitals compare in their rates of postoperative complications following a particular operation. As some hospitals carry out the operation commonly, while other hospitals perform the operation rarely, the accuracy with which the complication rates are estimated will vary considerably from hospital to hospital. Consequently, if the hospitals are ordered according to their complication rates, some may appear to be outliers compared with other hospitals, purely due to chance variation. When mixed models are used to analyse data of this type, the estimates of the complication rates are adjusted to allow for the number of operations, and rates based on small numbers become less extreme.
- Example 4: Analysis of a multi-centre trial Many clinical trials are organised on a multi-centre basis, usually because there is an inadequate number of suitable patients in any single centre. The analysis of multi-centre trials often ignores the centres from which the data were obtained, making the implicit assumption that all centres are identical to one another. This assumption may sometimes be dangerously misleading. For example, a multi-centre trial comparing two surgical treatments for a condition could be expected to show major differences between centres. There could be two types of differences. First, the centres may differ in the overall success, averaged over the two surgical treatments. More importantly, there may be substantial differences in the relative benefit of the two treatments across different centres. Surgeons who have had more experience with one operation (A) may produce better outcomes with A, while surgeons with more experience with the alternative operation (B) may obtain better results with B. Mixed models can provide an insightful analysis of such a trial by allowing for the extent to which treatment effects differ from centre to centre. Even when the difference between treatments can be assumed to be identical in all centres, a mixed model can improve the precision of the treatment estimates by taking appropriate account of the centres in the analysis.
- Example 5: Repeated measurements over time In a clinical trial, the response to treatment is often assessed as a series of observations over time. For example, in a trial to assess the effect of a drug in reducing blood pressure, measurements might be taken at two, four, six and eight weeks after starting treatment. The analysis will usually be complicated by a number of patients failing to appear for some assessments or withdrawing from the study before it is complete. This complication can cause considerable difficulty in a conventional analysis. A mixed models analysis of such a study does not require complete data from all subjects. This results in more appropriate estimates of the effect of treatment and their standard errors (SEs). The mixed model also gives great flexibility in analysis, in that it can allow for a wide variety of ways in which the successive observations are correlated with one another.
1.2 Introductory example
We consider a very simple cross-over trial using artificial data. In this trial, each patient receives each of treatments A and B for a fixed period. At the end of each treatment period, a measurement is taken to assess the response to that treatment. In the analysis of such a trial, we commonly refer to treatments being crossed with patients, meaning that the categories of ‘treatments’ occur in combination with those of ‘patients’. For the purpose of this illustration, we will suppose that the response to each treatment is unaffected by whether it is received in the first or second period. The table shows the results from the six patients in this trial.
| Treatment | ||||
| Patient | A | B | Difference A − B | Patient mean |
| 1 | 20 | 12 | 8 | 16.0 |
| 2 | 26 | 24 | 2 | 25.0 |
| 3 | 16 | 17 | −1 | 16.5 |
| 4 | 29 | 21 | 8 | 25.0 |
| 5 | 22 | 21 | 1 | 21.5 |
| 6 | 24 | 17 | 7 | 20.5 |
| Mean | 22.83 | 18.67 | 4.17 | 20.75 |
1.2.1 Simple model to assess the effects of treatment (Model A)
We introduce in this section a very simple example of a statistical model using this data. A model can be thought of as an attempt to describe quantitatively the effect of a number of factors on each observation. Any model we describe is likely to be a gross oversimplification of reality. In developing models, we are seeking ones which are as simple as possible but which contain enough truth to ask questions of interest. In this first simple model, we will deliberately be oversimplistic in order to introduce our notation. We just describe the effect of the two treatments. The model may be expressed as
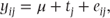
where
- j = A or B,
- yij = observation for treatment j on the ith patient,
- μ = overall mean,
- tj = effect of treatment j,
- eij = error for treatment j on the ith patient.
The constant μ represents the overall mean of the observations. μ + tA corresponds to the mean in the treatment group A, while μ + tB corresponds to the mean in the treatment group B. The constants μ, tA and tB can thus be estimated from the data. In our example, we can estimate the value of μ to be 20.75, the overall mean value. From the mean value in the first treatment group, we can estimate μ + tA as 22.83, and hence our estimate of tA is 22.83 − 20.75 = 2.08. Similarly, from the mean of the second treatment group, we estimate tB as −2.08. The term tj can therefore be thought of as a measure of the relative effect that treatment j has had on our outcome variable.
The error term, eij, or residual is what remains for each patient in each period when μ + tj is deducted from their observed measurement. This represents random variation about the mean value for each treatment. As such, the residuals can be regarded as the result of drawing random samples from a distribution. We will assume that the distribution is Gaussian or normal, with standard deviation σ, and that the samples drawn from the distribution are independent of each other. The mean of the distribution can be taken as zero, since any other value would simply cause a corresponding change in the value of μ. Thus, we will write this as
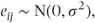
where σ2 is the variance of the residuals. In practice, checks should be made to determine whether this assumption of normally distributed residuals is reasonable. Suitable checking methods will be considered in Section 2.4.6. As individual observations are modelled as the sum of μ + tj, which are both constants, and the residual term, it follows that the variance of individual observations equals the residual variance:
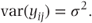
The covariance of any two separate observations yij and 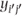 can be written as
can be written as
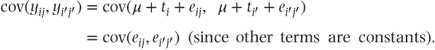
Since all the residuals are assumed independent (i.e. uncorrelated), it follows that
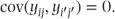
The residual variance, σ2, can be estimated using a standard technique known as analysis of variance (ANOVA). The essence of the method is that the total variation in the data is decomposed into components that are associated with possible causes of this variation, for example, that one treatment may be associated with higher observations, with the other being associated with lower observations. For this first model, using this technique, we obtain the following ANOVA table:
| Source of variation | Degrees of freedom | Sums of squares | Mean square | F | p |
| Treatments | 1 | 52.08 | 52.08 | 2.68 | 0.13 |
| Residual | 10 | 194.17 | 19.42 |
Note: F = value for the F test (ratio of mean square for treatments to mean square for residual).
p = significance level corresponding to the F test.
The residual mean square of 19.42 is our estimate of the residual variance, σ2, for this model. The key question often arising from this type of study is as follows: ‘do the treatment effects differ significantly from each other?’ This can be assessed by the F test, which assesses the null hypothesis of no mean difference between the treatments (the larger the treatment difference, the larger the treatment mean square and the higher the value of F). The p value of 0.13 is greater than the conventionally used cutoff point for statistical significance of 0.05. Therefore, we cannot conclude that the treatment effects are significantly different. The difference between the treatment effects and the SE of this difference provides a measure of the size of the treatment difference and the accuracy with which it is estimated:
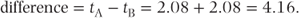
The SE of the difference is given by the formula
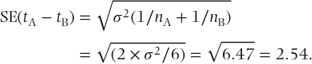
Note that a t test can also be constructed from this difference and SE, giving t = 4.16/2.54 = 1.63. This is the square root of our F statistic of 2.68 and gives an identical t test p value of 0.13.
1.2.2 A model taking patient effects into account (Model B)
Model A as discussed previously did not utilise the fact that pairs of observations were taken on the same patients. It is possible, and indeed likely, that some patients will tend to have systematically higher measurements than others, and we may be able to improve the model by making allowance for this. This can be done by additionally including patient effects into the model:
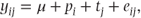
where pi are constants representing the ith patient effect.
The ANOVA table arising from this model is as follows:
| Source of variation | Degrees of freedom | Sums of squares | Mean square | F | p |
| Patients | 5 | 154.75 | 30.95 | 3.93 | 0.08 |
| Treatments | 1 | 52.08 | 52.08 | 6.61 | 0.05 |
| Residual | 5 | 39.42 | 7.88 |
The estimate of the residual variance, σ2, is now 7.88. It is lower than in Model A because it represents the ‘within-patient’ variation, as we have taken account of patient effects. The F test p value of 0.05 indicates that the treatment effects are now significantly different. The difference between the treatment effects is the same as in Model A, 4.16, but its SE is now as follows:
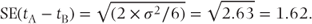
(Note that the SE of the treatment difference could alternatively have been obtained directly from the differences in patient observations.)
Model B is perhaps the ‘obvious’ one to think of for this dataset. However, even in this simple case, by comparison with Model A we can see that the statistical modeller has some flexibility in his/her choice of model. In most situations, there is no single ‘correct’ model, and, in fact, models are rarely completely adequate. The job of the statistical modeller is to choose that model which most closely achieves the objectives of the study.
1.2.3 Random effects model (Model C)
In the Models A and B, the only assumption we made about variation was that the residuals were normally distributed. We did not assume that patient or treatment effects arose from a distribution. They were assumed to take constant values. These models can be described as fixed effects models, and all effects fitted within them are fixed effects.
An alternative approach available to us is to assume that some of the terms in the model, instead of taking constant values, are realisations of values from a probability distribution. If we assumed that patient effects also arose from independent samples from a normal distribution, then the model could be expressed as
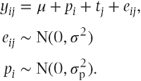
The pi are now referred to as random effects. Such models, which contain a mixture of fixed and random effects, provide an example of a mixed model. In this book, we will meet several different types of mixed model, and we describe in Section 1.5 the common feature that distinguishes them from fixed effects models. To distinguish the class of models we have just met from those we will meet later, we will refer to this type of model as a random effects model.
Each random effect in the model gives rise to a variance component. This is a model parameter that quantifies random variation due to that effect only. In this model, the patient variance component is 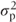 . We can describe variation at this level (between patients) as occurring within the patient error stratum (see Section 1.6 for a full description of the error stratum). This random variation occurs in addition to the residual variation (the residual variance can also be defined as a variance component.)
. We can describe variation at this level (between patients) as occurring within the patient error stratum (see Section 1.6 for a full description of the error stratum). This random variation occurs in addition to the residual variation (the residual variance can also be defined as a variance component.)
Defining the model in this way causes some differences in its statistical properties compared with the fixed effects model met earlier.
The variance of individual observations in a random effects model is the sum of all the variance components. Thus,
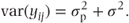
This contrasts with the fixed effects models where we had
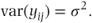
The effect on the covariance of pairs of observations in the random effects model is interesting and perhaps surprising. Since yij = μ + pi + tj + eij, we can write
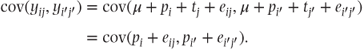
When observations from different patients are being considered (i.e. i ≠ i′), because of the independence of the observations, 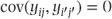 . However, when two samples from the same patient are considered (i.e. i = i′), then
. However, when two samples from the same patient are considered (i.e. i = i′), then
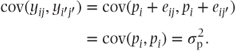
Thus, observations on the same patient are correlated and have covariance equal to the patient variance component, while observations on different patients are uncorrelated. This contrasts with the fixed effects models where the covariance of any pair of observations is zero.
The ANOVA table for the random effects model is identical to that for the fixed effects model. However, we can now use it to calculate the patient variance component using results from the statistical theory that underpins the ANOVA method. The theory shows the expected values for each of the mean square terms in the ANOVA table, in terms of σ2, 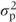 and the treatment effects. These are tabulated in the following table. We can now equate the expected value for the mean squares expressed in terms of the variance components to the observed values of the mean squares to obtain estimates of σ2 and
and the treatment effects. These are tabulated in the following table. We can now equate the expected value for the mean squares expressed in terms of the variance components to the observed values of the mean squares to obtain estimates of σ2 and 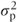 .
.
| Source of variation | Degrees of freedom | Sums of squares | Mean square | E(MS) |
| Patients | 5 | 154.75 | 30.95 | 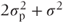 |
| Treatments | 1 | 52.08 | 52.08 | 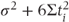 |
| Residual | 5 | 39.42 | 7.88 | σ2 |
Note: E(MS) = expected mean square.
Thus, from the residual line in the ANOVA table, 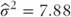 . In addition, by subtracting the third line of the table from the first we have:
. In addition, by subtracting the third line of the table from the first we have:
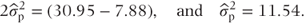
(We are introducing the notation 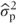 to denote that this is an estimate of the unknown
to denote that this is an estimate of the unknown 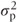 , and
, and 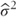 is an estimate of σ2.)
is an estimate of σ2.)
In this example, we obtain identical treatment effect results to those for the fixed effects model (Model B). This occurs because we are, in effect, only using within-patient information to estimate the treatment effect (since all information on treatment occurs in the within-patient residual error stratum). Again, we obtain the treatment difference as −4.16 with a SE of 1.62. Thus, in this case, it makes no difference at all to our conclusions about treatments whether we fit patient effects as fixed or random. However, had any of the values in the dataset been missing, this would not have been the case. We now consider this situation.
Dataset with missing values
We will now consider analysing the dataset with two of the observations set to missing.
| Treatment | ||||
| Patient | A | B | Difference A − B | Patient mean |
| 1 | 20 | 12 | 8 | 16.0 |
| 2 | 26 | 24 | 2 | 25.0 |
| 3 | 16 | 17 | −1 | 16.5 |
| 4 | 29 | 21 | 8 | 25.0 |
| 5 | 22 | – | – | 22.0 |
| 6 | – | 17 | – | 17.0 |
| Mean | 4.25 | |||
As shown previously, there are two ways we can analyse the data. We can base our analysis on a model where the patient effects are regarded as fixed (Model B) or can regard patient effects as random (Model C).
The fixed effects model For this analysis, we apply ANOVA in the standard way, and the result of that analysis is summarised as follows:
| Source of variation | Degrees of freedom | Sums of squares | Mean square | F | p |
| Patients | 5 | 167.90 | 33.58 | 3.32 | 0.18 |
| Treatments | 1 | 36.13 | 36.13 | 3.57 | 0.16 |
| Residual | 3 | 30.38 | 10.12 |
In the fitting of Model B, it is interesting to look at the contribution that the data from patient 5 are making to the analysis. The value of 22 gives us information that will allow us to estimate the level in that patient, but it tells us nothing at all about the difference between the two treatments, nor does it even tell us anything about the effect of treatment A, which was received, because all the information in the observed value of 22 is used up in estimating the patient effect. The same comment applies to the data from patient 6.
Thus, in this fixed effects model, the estimate of the mean treatment difference, 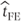 , will be calculated only from the treatment differences for patients 1–4 who have complete data:
, will be calculated only from the treatment differences for patients 1–4 who have complete data:
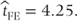
The variance of 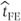 can be calculated from the residual variance,
can be calculated from the residual variance, 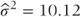 , as
, as
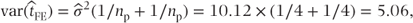
where np is the number of observations with data on treatments A and B. The SE of the treatment difference is 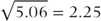 .
.
The random effects model When patient effects are fitted as random, the variance components cannot be derived in a straightforward way from an ANOVA table since the data are unbalanced. They are found computationally (using PROC MIXED, a SAS procedure, which is described in more detail in Chapter 9) as
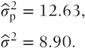
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


