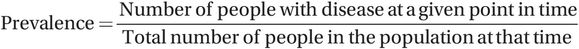The goal of public health is to improve the overall health of a population by reducing the burden of disease and premature death. To do this we need to be able to quantify the levels of ill-health or disease in a population in order to monitor our progress towards eliminating existing problems and to identify the emergence of new problems. Many different measures are used by researchers and policy makers to describe the health of populations. You have already met some of these for example the attack rate, which was used to investigate the source of the food poisoning outbreak in the previous chapter. In this chapter we will introduce some more of the most commonly used measures so that you can use and interpret them correctly. We will first discuss the three fundamental measures that underlie both the attack rate and most of the other health statistics that you will come across in health-related reports, the incidence rate, incidence proportion (also called risk or cumulative incidence) and prevalence, and will then look at how they are calculated and used in practice. We will finish by considering some other more elaborate measures that attempt to get closer to describing the overall health of a population. As you will see, this is not always as straightforward as it might seem.
What are we measuring?
Before we can start to measure disease, we have to have a very clear idea of what it is that we are trying to determine. In general, the diagnosis of disease is based on a combination of symptoms, subjective indications of disease reported by the person themselves; signs, objective indications of disease apparent to the physician; and additional tests. Criteria for making a diagnosis can be very simple: the presence of antibodies against an infectious agent can indicate infection, and diagnosis of most cancers is fairly straightforward on the basis of tissue histology (examination with a light microscope); but for some diseases, particularly mental health conditions such as depression, the diagnostic criteria are much more complex, involving combinations of signs and symptoms.
For health data to be meaningful, diagnostic criteria leading to a case definition have to be clear, unambiguous and easy to use under a wide range of circumstances. It is important to remember that different case definitions can lead to very different pictures. As shown in Figure 2.1, a study in the United Arab Emirates showed that the prevalence of gestational diabetes (diabetes during pregnancy) in a group of 3500 women was much higher using one set of criteria to diagnose diabetes (Carpenter’s criteria, 30.4%) than another (O’Sullivan’s criteria, 20.2%) (Agarwal and Punnose, 2002). Such differences obviously have major implications for health care planners. If you want to compare information from different reports the first thing to check is that you are comparing apples with apples – have they all measured the same thing using the same criteria? This can be a particular problem when trying to compare patterns of disease over time because changes in diagnostic criteria can lead to sudden increases or decreases in the number of cases recorded, and you will see a dramatic example of this in Chapter 3. It is also important to consider how good the measurements are, and we will look at this and the implications of poor measurement in more detail in Chapter 7. For the rest of this chapter, however, we will assume that we know what we want to measure and that we can measure it accurately.
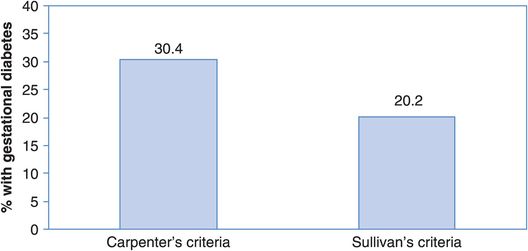
Percent of population with gestational diabetes according to two sets of diagnostic criteria.
The concepts: prevalence and incidence
Once we have defined what we mean by disease,1 we can go on to measure how often it occurs.
In Table 2.1 we see the estimated number of people infected with HIV in the various regions of the world at the end of 2012, and the number of new cases of HIV infection that occurred during 2012. These data clearly show the huge burden borne by Sub-Saharan Africa, which has six times the number of cases of any other region, but what can they tell us about the relative importance of HIV in other regions? The East Asia and Western/Central Europe regions both had almost 900,000 people infected with HIV at the end of 2012. How can we describe and compare the burden of HIV in these populations more fully?
| Region | Population (×1000) | People living with HIV (end of 2012) | New HIV infections (2012) |
|---|---|---|---|
| Sub-Saharan Africa | 867,000 | 25,000,000 | 1,600,000 |
| East Asia | 1,554,400 | 880,000 | 81,000 |
| Oceania | 34,200 | 51,000 | 2100 |
| South and Southeast Asia | 2,286,000 | 3,900,000 | 270,000 |
| Eastern Europe & Central Asia | 278,900 | 1,300,000 | 130,000 |
| Western and Central Europe | 608,200 | 860,000 | 29,000 |
| North Africa & Middle East | 319,500 | 260,000 | 32,000 |
| North America | 348,800 | 1,300,000 | 48,000 |
| Caribbean | 36,300 | 250,000 | 12,000 |
| Latin America | 557,000 | 1,500,000 | 86,000 |
| TOTAL | 6,890,300 | 35,301,000 | 2,290,100 |
What percentage of people in Western and Central Europe were living with HIV at the end of 2012?
At the end of 2012, 860,000 of the 608,200,000 people in Western and Central Europe or 0.14% of the population were living with HIV. During 2012, another 29,000 people or 0.0048% of the population became infected with HIV. Now 0.0048% is a very small number. It simply tells us that there were 0.0048 new HIV infections for every 100 people during 2012, so an alternative way to present the same information would be to multiply the numbers by 1000 and say that there were 4.8 new infections in every 100,000 people (4.8/100,000 or 4.8/105).2
What you calculated above were, first, the prevalence of existing HIV infections in Western and Central Europe at the end of 2012 and, second, the incidence of new HIV infections in the same region during 2012. These measures give us two different ways of quantifying the amount of disease in a population. Table 2.2 shows the same information for each of the regions. These data confirm the high levels of HIV infection in Sub-Saharan Africa and show us that, despite the relatively low number of new cases in the Caribbean, the small population there means that the incidence is also high. The data also show us that although the actual numbers of cases in East Asia and Western/Central Europe are similar, the prevalence per 100 people (%) is much lower in East Asia (0.06%) than in Western and Central Europe (0.14%). Like the beer example in Box 2.1, these data emphasise the need to take the size of a population into account when comparing it with others.
| Region | Population (×1000) | People living with HIV (end of 2012) | Prevalence (%) | New HIV infections (2012) | Incidence (per 100,000/year) |
|---|---|---|---|---|---|
| Sub-Saharan Africa | 867,000 | 25,000,000 | 2.88 | 1,600,000 | 184.5 |
| East Asia | 1,554,400 | 880,000 | 0.06 | 81,000 | 5.2 |
| Oceania | 34,200 | 51,000 | 0.15 | 2,100 | 6.1 |
| South and Southeast Asia | 2,286,000 | 3,900,000 | 0.17 | 270,000 | 11.8 |
| Eastern Europe & Central Asia | 278,900 | 1,300,000 | 0.47 | 130,000 | 46.6 |
| Western and Central Europe | 608,200 | 860,000 | 0.14 | 29,000 | 4.8 |
| North Africa & Middle East | 319,500 | 260,000 | 0.08 | 32,000 | 10.0 |
| North America | 348,800 | 1,300,000 | 0.37 | 48,000 | 13.8 |
| Caribbean | 36,300 | 250,000 | 0.69 | 12,000 | 33.0 |
| Latin America | 557,000 | 1,500,000 | 0.27 | 86,000 | 15.4 |
| TOTAL | 6,890,300 | 35,301,000 | 0.51 | 2,290,100 | 33.2 |
According to the Brewers Association of Japan, the Chinese drink the most beer in the world (44,201 million litres in 2012, up from 28,640 in 2004) followed by the Americans (24,186 million litres). In contrast, the Czech Republic ranked a lowly 21st in terms of total consumption (1905 million litres) and Ireland didn’t even make the top 25. This information may be useful for planning production, but do the Chinese and Americans really drink more beer than the rest of us? An alternative and possibly more informative way to look at these data is in terms of consumption per capita. When we do this, the USA falls to 14th position in the ‘beer drinking league table’ (77 litres per capita) and China falls way off the screen (a mere 33 litres per capita). The Czechs are now the champions (149 litres per capita), followed by Austria (108 litres) and Germany (106 litres) in 2nd and 3rd place and Ireland comes in 6th place (98 litres per capita). While Australia held the 4th spot in 2004 with an average of 110 litres per capita, by 2012 they had fallen to 11th on the table (83 litres).
We will now look at these measures in more detail.
Prevalence
The prevalence of a disease tells us what proportion of a population actually has the disease at a specific point in time: an estimated 0.14% or 140 of every 100,000 people in Western and Central Europe were living with HIV at the end of 2012. This is a snapshot of the situation at a single point in time and, for this reason, it is sometimes called the ‘point’ prevalence. Note that you may also see references to ‘period prevalence’ which measures the proportion of the population that had the disease at any time during a specified period. This is a complex measure that combines the prevalence (everybody who had the disease at the start of the period) and incidence (all of the new cases of disease during the period).
Percentages can be confusing because there is often more than one way in which they can be calculated and this can lead to problems with interpretation – see Box 2.2 for some additional guidance.
Imagine a study that gave the following results:
| Asthma | No asthma | Total | |
|---|---|---|---|
| Non-smokers | 40 | 360 | 400 |
| Smokers | 30 | 170 | 200 |
| Total | 70 | 530 | 600 |
There are two ways that we can look at these data. One way would be to calculate the percentages of (a) non-smokers and (b) smokers who have asthma – these are row percentages because we use the total of each row, the number of non-smokers or smokers, as the denominator (note: the denominator is the bottom half of a fraction and the numerator the top half):
| Asthma | No asthma | Total | |
|---|---|---|---|
| Non-smokers | 40 ÷ 400 = 10% | 360 ÷ 400 = 90% | 400 = 100% |
| Smokers | 30 ÷ 200 = 15% | 170 ÷ 200 = 85% | 200 = 100% |
This tells us that 10% of non-smokers and 15% of smokers have asthma.
Alternatively, we could use the same data to calculate the percentages of people with and without asthma who smoke – these are column percentages because now we use the total of each column, the number of people with or without asthma, as the denominator:
| Asthma | No asthma | |
|---|---|---|
| Non-smokers | 40÷70 = 57% | 360 ÷ 530 = 68% |
| Smokers | 30÷70 = 43% | 170 ÷ 530 = 32% |
| Total | 70 = 100% | 530 = 100% |
This tells us that 43% of people with asthma and only 32% of people without asthma are smokers.
It is very important to decide first which percentages are most relevant for a particular situation and then to calculate and interpret the percentages correctly. Saying that 43% of people with asthma are smokers (correct) is not the same as saying that 43% of smokers have asthma (incorrect; 15% of smokers have asthma).
Prevalence measures are just one number (the number of people with disease) divided by another number (the total number of people in the population). They have no units, and are mostly reported simply as a proportion or a percentage (2.9% of Sub-Saharan Africans were living with HIV at the end of 2012), but may also be shown as cases/population, for example 370/100,000 North Americans were living with HIV at the end of 2012. Note that a more precise answer for the proportion of Sub-Saharan Africans with HIV is 0.02883506… or 2.883506% but, for simplicity, we have rounded this to one decimal place giving 2.9%. Although you will often see the term ‘prevalence rate’, this is not a true rate because a rate should include units of time. An example of a true rate is the use of distance travelled per hour, i.e. kph or mph, to measure the speed of a car. The time point at which people are counted should, however, always be reported when giving an estimate of prevalence. This is often a fixed point in calendar time, such as 31 December 2015, but it can also be a fixed point in life, for instance, birth or retirement. For example, if 1000 babies were born alive in one hospital in a given year and, of these, five babies were born with congenital abnormalities, we would say that the prevalence of congenital abnormality at birth was 5/1000 live births in that year. Prevalence can be expressed per 100 people (per cent, %) or per 1000 (103), 10,000 (104) or 100,000 (105). It doesn’t matter as long as it is clear which is being used.
Rounding: If the first number that is cut off is between 0 and 4 you round down and if it is between 5 and 9 you round up. Here we rounded 2.8835 up to 2.9, but if it had been 2.8435 we would have rounded down to 2.8. In practice it is rarely necessary to show results to more than two or three ‘significant’ figures (e.g. 2900, 2.9, 0.0029 are all rounded to 2 significant figures), unless we are confident the additional numbers are both accurate and important.
In practice, it would be rare to identify all prevalent cases of disease at one precise point in time; e.g. a blood pressure survey may take weeks or months to conduct, given limited numbers of researchers, amounts of equipment and availability of those being measured. The exact size of the population may also not be known on a given day and this might well be based on an estimate or projection from the most recent census data.
Incidence
The incidence of disease measures how quickly people are developing the disease and it differs from prevalence because it considers only new infections, sometimes called incident cases, that occurred in a specific time period. During 2012, 1.6 million people in Sub-Saharan Africa or 0.18% of the population were newly diagnosed as HIV-positive. Another way of saying this is that the incidence of HIV infection was 184.5/100,000 per year (Table 2.2). You will find that people use the term ‘incidence’ on its own to mean slightly different things – some use it for the number of new cases (i.e. 1.6 million), some for the proportion of people who are newly infected (i.e. 0.0018 or 0.18%) and some for the rate at which new infection has occurred (i.e. 184.5 new cases per 100,000 people per year). To avoid confusion we will describe the latter measure as the incidence rate which, unlike measures of prevalence, is a true rate because it includes a measure of time.
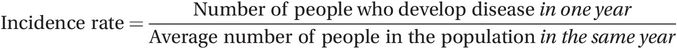 (2.2)
(2.2)We will look further at how to calculate these measures later, but first let us consider the concept of the ‘population at risk’ and the relationship between prevalence and the incidence rate.
Population at risk
In the example above it is probably not unreasonable to assume that everyone in the population might be at risk of contracting HIV, although, obviously, some groups will be more ‘at risk’ than others; but what if the disease of interest were something like cervical cancer? To use the whole population to calculate rates of cancer of the cervix (the neck of the uterus) would be inappropriate, because a man could never develop the disease. We would calculate a sex-specific rate by dividing the number of cases by the number of women in the population. However, many women will have had a hysterectomy (removal of the uterus). They are then no longer at risk of developing cervical cancer and so, strictly speaking, should not be included in the population at risk. In practice, published rates of both cervical and endometrial cancer (cancer of the lining of the uterus) rarely allow for this so it is difficult to compare the rates of these cancers between countries that have very different hysterectomy rates. We discussed above the importance of making sure that different reports used the same definition of disease (i.e. they counted the same thing in the numerator); it is also crucial to ensure that the denominators represent equivalent populations (e.g. they are similar in age, sex distribution, etc.).
The relationship between incidence and prevalence
If two diseases have the same incidence, but one lasts three times longer than the other, then, at any point in time, you are much more likely to find people suffering from the more long-lasting disease. Very crudely (and assuming that people do not move into or out of the area), the relationship between prevalence (P) and the incidence rate (IR) depends on how long the disease persists before cure or death (average duration of disease, D):
where ≈ means approximately equal to. (Box 2.3 shows a more accurate version of this formula.)
The relationship P ≈ IR × D is approximately true in what is called a stationary population where the number of people entering the population (immigration and birth) balances the number of people leaving (emigration and death). A second requirement is that the prevalence of disease must be low (less than about 10%). This is the case for many diseases, but a more general formula that does not require the disease to be rare is
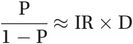 (2.4)
(2.4)where P is the prevalence of disease expressed as a proportion and 1 – P is the proportion of non-diseased people; e.g. if the prevalence (P) is 2% or 0.02 then 1 – P is 0.98.
For example, in the USA in 2009, the incidence of hepatitis A was relatively high with an estimated 21,000 new infections (CDC Division of Viral Hepatitis, 2009) and almost one-third of the population may have been infected at some time. However, because it is an acute infection and people recover fairly quickly, the prevalence of hepatitis A infection at any one point in time would be quite low. In contrast, hepatitis C infection is less common (approximately 16,000 new infections in 2009) but most of those infected develop a chronic infection and are infected for life. This means that the prevalence of hepatitis C is much higher with between 2.7 and 3.9 million Americans estimated to be living with chronic infection.
Hepatitis A infection rates have been falling in the USA since the introduction of infant and child vaccination, while reported cases of hepatitis C have increased.
If the new treatment meant that people were cured more quickly and so were ill for less time, then the prevalence would fall. However, if the disease had previously been fatal and the new treatment meant that people lived longer with the disease, then the prevalence would increase. In general, a new treatment will not affect the incidence of a disease. The only exception to this rule might be for an infectious disease: if people were ill and thus infectious for less time, they might pass the infection to fewer people and so the incidence would fall.
As you can see, the prevalence of a disease reflects a balance of several factors. If the incidence of a disease increases then the prevalence will also increase; if the duration of sickness changes then the prevalence will change. This means that the prevalence of a disease is generally not the best way to measure the underlying forces driving the occurrence of the disease – we must use the incidence rate for this. Nonetheless, prevalence is useful for measuring diseases that have a gradual onset and long duration such as type-2 diabetes and osteoarthritis, and also for capturing the frequency of congenital malformations at birth. Both prevalence and incidence are of direct value for describing the overall disease burden of a population and, together with simple counts of the numbers of cases of disease, are fundamentally important for assessing health care needs and planning health services.
Measuring disease occurrence in practice: epidemiological studies
As we discussed above, the occurrence of disease can be quantified by looking at the prevalence or the incidence rate. We will now consider these further, together with an alternative way of measuring incidence known as the incidence proportion (or risk or cumulative incidence). These three fundamental measures form the basis of descriptive epidemiology, which seeks to answer the first four of the five core questions that you met in Chapter 1: What (diseases are occurring)? Who (is getting them)? Where? and When? The measures can all be calculated from routinely collected data (as in the HIV example above) or from studies conducted specifically to measure the incidence or prevalence of disease, and they are widely used in health reports around the world. We will come back to the use of routine data below and for now will concentrate on how we measure the occurrence of disease in an epidemiological study.
To measure the prevalence of disease we need to conduct a survey, or what is often called a cross-sectional study, in which a random sample (or cross-section) of the population is questioned or assessed to ascertain whether they have a particular condition at a given point in time. To measure the incidence of disease we need to start with a group (or cohort) of people who are free of the disease of interest but who are ‘at risk’ of developing it. We then follow them over time to see who actually develops the disease (a cohort study; e.g. the British Doctors Study mentioned in Chapter 1).
When we conduct a research study we can specify exactly who is in the study and can usually collect individual data for all (or most) of those people. We can therefore identify who is ‘at risk’ and calculate quite accurate measures of disease incidence (or prevalence). We can also relate the occurrence of disease to its potential causes to answer the final question, Why?, and we will consider this aspect further in Chapter 5.
Consider, for example, a study conducted in a hypothetical primary school with 100 pupils. Imagine that, on the first day of the new term, nine children had a cold. Over the next week another seven children developed a cold.
What percentage of children had a cold on the first day of term?
What percentage of the children who didn’t have a cold on the first day of term developed one during the next week?
The first measure that you calculated is the prevalence of the common cold in this group of children: 9 out of 100 children or 9% had a cold on the first day of term. The second measure is known as the incidence proportion or risk of colds: out of 91 children ‘at risk’ of developing a cold (i.e. they did not have one already), 7 or 7.7% developed one during the first week of term. The denominator (population at risk) is 91 in this case because 9 of the 100 children already had a cold and were not therefore ‘at risk’ of catching another at the same time. As its name suggests, the incidence proportion measures the proportion, or percentage, of people (children in this case) who were at risk of developing a cold and who did so during the period of the study (one week). Note that it is always important to specify the time period – a risk3 of 5% in 1 year would be very different from a risk of 5% in 20 years. The incidence proportion is sometimes known as the attack rate, especially when it refers to a short time period as, for example, in the context of an outbreak of infectious diseases like the food poisoning example in Chapter 1.
This example was simple because the common cold is just that, very common, and we were only interested in the children for one week. Imagine that we were trying to measure the incidence of a much rarer disease such as cancer. We would obviously need a much larger group of people and we would need to follow them for much longer to see who developed the cancer. In this situation it is very difficult to keep track of people and we would inevitably lose some from the study group and not know what happened to them. Another problem is that people will die from other ‘competing’ causes and so they will no longer be at risk of developing the cancer. In this situation, calculations of the incidence proportion may be inaccurate (or will become so over time) because we will not know exactly who has developed the disease. In practice, we can calculate this measure only when we have a clearly defined group of people who are all (or almost all) followed for the specified follow-up period.
When this is not the situation we use a different method to calculate an incidence rate. Instead of simply counting the actual number of people at risk of disease, we count up the length of time they were at risk of disease. Imagine that we followed a group of 1000 men for 5 years and that during this time 15 of them had a non-fatal heart attack. This gives us an incidence proportion or risk of 1.5% for the 5-year period. During this period the men have lived a total of 1000 × 5 = 5000 years of life or person-years. We could have obtained the same number of person-years by following a group of 5000 men for 1 year each, or a group of 500 men for 10 years each. Alternatively, we could have followed some men for one year, some for two years, some for three years, etc., to arrive at the same total of 5000. We are no longer so focussed on the actual number of people who were at risk of the disease, but rather on the total person-time4 (number of person-years) they were at risk. This not only gives us a much more accurate measure of how quickly disease is occurring among those at risk, but it also gives us much greater flexibility. Assuming that we still saw 15 heart attacks during our 5000 person-years (py), we could calculate the incidence rate as 15 per 5000 person-years or, more usually, 3 per 1000 or 300/100,000 person-years.
The incidence rate is also sometimes called the incidence density.
The incidence proportion (IP) (also known as cumulative incidence or risk) measures the proportion of people who develop disease during a specified period:
 (2.5)
(2.5)The incidence rate (IR) measures how quickly people are developing a disease:
 (2.6)
(2.6)Note that, although Equation (2.6) looks slightly different from Equation (2.2), they are measuring the same thing – if you are unsure about this, see Box 2.4 for an explanation of why this is true. We will also come back to this under ‘Crude incidence and mortality rates’ on page 49.
As you saw above, the ‘person-time’ method for calculating an incidence rate (Equation (2.6)) is particularly useful in research studies when different people have been followed for different lengths of time. However, at the population level we may be dealing with millions of people and it is clearly not feasible to calculate the person-time that each is at risk. Instead we usually calculate the incidence rate for a single year and work on the assumption that everyone in the population is at risk for the whole of that year (Equation (2.2)). The fundamental concept is, however, the same – if there are 500,000 people in the population and we assume they are all at risk for one year that is the same as 500,000 person-years. The only distinction is that the ‘routine rates’ calculated using Equation (2.2) are based on population averages, whereas the ‘epidemiological rates’ calculated using Equation (2.6) are based on adding together carefully measured units of individual person-time to give a precise denominator. The resulting incidence rates are also presented slightly differently: routine incidence rates are usually described per 100,000 people per year, whereas in epidemiological studies using individual data they are usually shown per 100,000 person-years. You will find that some people differentiate the rates calculated based on person-time by describing them as incidence density; however, we, as most others, will refer to both as incidence rates because they are effectively measuring the same thing.
In practice, it will usually only be possible to calculate the incidence rate one way. If data are available for individual people who have been followed for different lengths of time then we use Equation (2.6). If we only have summary data for a population then we use Equation (2.2).
Incidence rates versus incidence proportion
The distinction between an incidence proportion or risk and an incidence rate can be confusing. An analogy that we have found helpful is to think of these measures in terms of driving a car.
The incidence rate is equivalent to the average speed of a car at a particular point in time, e.g. 60 km/hour.
The incidence proportion is analogous to the distance travelled by a car during a specified interval of time, e.g. 60 km in one hour.
The distance a car travels depends both on its average speed and on the length of time it travels for. If a car travels at an average speed of 60 km/hour then it will cover 30 km in 30 minutes, 60 km in one hour, and so on. When we consider a time interval of one hour, the total distance travelled (60 km in one hour) looks very similar to the average speed because this is expressed per hour (60 km/hr). Distance and speed are, however, fundamentally different.
In the same way, the incidence rate describes the ‘speed’ at which new cases of disease are occurring, and therefore reflects what is sometimes called the underlying force of morbidity. As its name suggests, the incidence proportion measures the proportion of a group who develop the disease over a particular time and is thus a function both of the underlying incidence rate and of the length of follow-up. If the incidence rate is 10 per 100,000/year then the incidence proportion will be 10 cases in 100,000 (= 0.0001 or 0.01%) in one year, 20 cases in 100,000 (= 0.0002 or 0.02%) in two years, and so on. As with the car example, when we consider a time interval of one year, an incidence proportion expressed as 10 per 100,000 people in one year looks much like an incidence rate (10 per 100,000 per year or person-years) because we usually show incidence rates per year. It is important to recognise that, as with distance and speed, the measures are different. A good way to help avoid confusion is to ensure that the incidence proportion is expressed as a proportion (e.g. 0.0001) or percentage rather than ‘per 100,000’.
Example
Imagine that we identified a group of 10 healthy people on 1 January 2007 and that we decided to follow these people for seven years to see who developed a particular disease. Figure 2.2 shows the hypothetical experience of these people: four developed the disease of interest and three of them died, and another three were ‘lost to follow-up’ (e.g. they moved away or died of some other disease). Let us now look at how we would calculate the different measures of disease occurrence in this group.
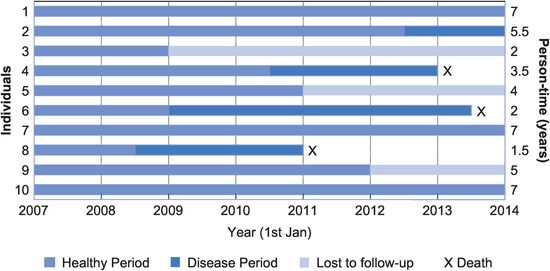
A hypothetical follow-up study.
Prevalence
Remember that prevalence tells us the proportion of the population who were sick at a particular point in time (Equation (2.1)). For example, on 1 January 2010, two people were sick out of the nine people left in our group on that date (one was lost to follow-up), so
Prevalence = 2 ÷ 9 = 22%
What was the prevalence of the disease on 30 June 2011?
On 30 June 2011 two people were sick but there were only seven people left in the group on that date (one had died and two had been lost to follow-up), so
Prevalence = 2 ÷ 7 = 29%
Incidence proportion (cumulative incidence)
This tells us the proportion of a population ‘at risk’ of developing a disease who actually became ill during a specified time interval (Equation (2.5)). It is also the probability or average risk that an individual will develop the disease during the period: if 30% of people in a population develop a disease then each individual has a 30% chance of developing it themselves. It is important to note that this is the average risk for the population, the risk for any individual is either zero (they won’t develop the disease) or one (they will).5 With the exception of some rare genetic diseases such as Huntington’s disease where all those who carry the aberrant gene will eventually develop the disease, this individual risk is usually unknown or unknowable, making accurate predictions for individuals in the clinical setting almost impossible.
In the example, 4 of the 10 people who were at risk at the start of the study developed the disease, but three were lost to follow-up and we do not know whether they developed the disease. This means that we cannot accurately calculate the incidence proportion or risk at seven years, but a minimum estimate would be
IP = 4 ÷ 10 = 40% in seven years
This is assuming that none of those lost to follow-up developed the disease. If any of them had developed the disease then the true risk would have been higher than 40%. The maximum estimate of the incidence proportion would assume that all three of the missing people developed the disease:
IP = 7 ÷ 10 = 70% in seven years
Note that we could calculate an accurate incidence proportion at two years – because we do have complete follow-up to that point:
IP = 1 ÷ 10 = 10% in two years
One type of study in which the study group is clearly defined and loss to follow-up is usually minimal is a clinical trial (see Chapter 4) and this means that the incidence proportion is an appropriate and common measure of outcome in this type of study. However, the field of clinical epidemiology has developed its own terminology for what we call the incidence proportion (see Box 2.5).

Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree