(1)
INSERM U554, Centre de Biochimie Structurale, Montpellier, France
(2)
Centre de Biochimie Structurale, INSERM U554, Montpellier, France
Abstract
Fluorescence is the most widely used technique to study the effect of pressure on biochemical systems. The use of pressure as a physical variable sheds light into volumetric characteristics of reactions. Here we focus on the effect of pressure on protein solutions using a simple unfolding example in order to illustrate the applications of the methodology. Topics covered in this review include the relationships between practical aspects and technical limitations; the effect of pressure and the study of protein cavities; the interpretation of thermodynamic and relaxation kinetics; and the study of relaxation amplitudes. Finally, we discuss the insights available from the combination of fluorescence and other methods adapted to high pressure, such as SAXS or NMR. Because of the simplicity and accessibility of high-pressure fluorescence, the technique is a starting point that complements appropriately multi-methodological approaches related to understanding protein function, disfunction, and folding from the volumetric point of view.
Key words
High-pressure fluorescenceProtein volumetric propertiesProtein foldingProtein cavities1 Introduction
The purpose of this note is to state a fact of possible biological interest which I have discovered incidentally in the course of other work. If the white of an egg is subjected to hydrostatic pressure at room temperature*, it becomes coagulated, presenting an appearance much like that of a hard-boiled egg.
P. W. BRIDGMAN, 1914 J Biol Chem 19, 511–512 (*N.B.7 kbar during 30 min)
Beyond the accepted interest for the understanding of life in extreme habitats [1–3], the utilization of high pressure (HP) to study biochemical equilibria yields precise insights into reaction volumes:
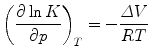
where K is the equilibrium constant, p the pressure, ΔV the difference of the final and initial partial molar volumes of the reactants (final minus initial), and RT the product of the molar gas constant and the temperature. HP studies can make a significant contribution to the general understanding of protein folding [4] and protein function (see ref. 5 for a textbook review). Since the observation of HP-induced boiling of the white of an egg by a hundred years ago [6], numerous apparatus have been adapted to work under pressure in order to assess diverse reaction coordinates of protein processes [5]. These innovations include turbidity spectrometers [7], fluorometers and absorbance spectrophotometers [8], fluorescence correlation (FCS) microscopes [9], circular dichroism [10, 11] and Fourier-transform infrared (FTIR) [12, 13] instruments, electron paramagnetic resonance (EPR) [14] and nuclear magnetic resonance (NMR) [15–17] spectrometers, X-ray diffractometers [18], small-angle X-ray scattering (SAXS) [19, 20] and neutron small-angle scattering (SANS) [21] devices, electrospray ionization mass spectrometers [22], electrophoresis apparatus [23], and calorimeters [24]. Due to this continual technical HP development, novel insights into protein physical chemistry have been forthcoming regarding folding [17, 25], refolding from aggregates [26–28], miss-folding [29], subunit dissociation, e.g., [30–40], dynamics [41], phase diagrams [37, 42–46], and interactions with lipids [47], DNA, e.g., [48, 49] or chemical compounds [38, 49–54].
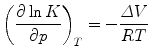
(1)
Today the combination of HP-fluorescence with other techniques is no longer carried out by distinct groups on different systems. Rather collective research efforts in the HP field have become the norm, as opposed to the exception [55, 56]. For example, the combination of HP-FTIR, HP-SAXS, and HP-crystallography ensured the volumetric characterization attained by HP-fluorescence on the effect of single mutants perturbing cavities [20, 57–59]. Contrary to protein perturbations by temperature, pH, or denaturants, pressure is considered a more gentle perturbation, leading to fully reversible events even at elevated protein concentrations (>1 mM) [7, 15, 42, 60–68]. This is because pressure acts non-thermally [69] by eliminating internal solvent-excluded void volumes at subunit interfaces or internal cavities, thus leading to pressure-induced dissociation [29], or unfolding [21, 70, 71]. Because it is technically and theoretically rather straightforward, in addition to being rapid and sensitive, fluorescence spectroscopy is widely used in the field of protein biophysics [72]. These attributes greatly facilitated the extension of fluorescence to the high-pressure field, and account for its early use.
The use of protein fluorescence spectroscopy in combination with pressure as a physical variable has been reviewed in detail elsewhere [23, 25, 63, 69, 73–78]. Given the recent renewed interest in pressure perturbation, our present aim is to revisit HP-fluorescence methodology in order to render the approach accessible to researchers and students from diverse academic backgrounds. For this purpose, we describe the potentiality and limitations of the technique by illustrating pressure denaturation by HP-fluorescence using the model monomeric and globular protein system, staphylococcal nuclease (SNase) [12, 21, 44, 79–89]. This example will allow us to consider thermodynamic (Subheading 3.1) and kinetic (Subheading 3.2) parameterization of the volumetric differences between the folded state, the transition state ensemble (TSE), and unfolded state via equilibrium pressure-induced unfolding and pressure-jump (P-jumps) relaxation studies, respectively. Additionally we will introduce to HP-fluorescence the linking between thermodynamics and kinetics by analysis of relaxation kinetics amplitudes [90, 91]. Our current understanding of the effect of pressure on proteins allows extension of HP-fluorescence information to more complex systems and/or higher resolution methods, e.g., single-molecule HP FCS or residue-specific HP NMR.
2 Materials
HP-fluorescence experiments involve similar materials as standard fluorescence, e.g., ultrapure reagents for buffers, pure protein samples, faultless quartz cuvettes, and so on. However specific technical care must be taken regarding the effect of pressure itself and the HP-equipment setup. In this section, we describe in detail the architecture and operation of the HP setup (Fig. 1) and we refer to Subheading 4 where technical issues and or tips are given. We note that the pressure limitation of the equipment is that of its lowest pressure component. In our system, the pump and lines and valves are limited to 60,000 psi (~4.5 kbar) whereas the cell itself is rated at 7 kbar.
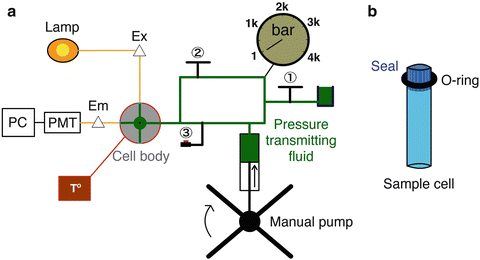

Fig. 1
Schematic sketch of HP-fluorescence apparatus. (a) Pressure is generated when the HP system is hermetic, manual valve (1)closed, by compression of the pressure-transmitting fluid (colored in green) via the action of the manual pump. (b) The sample cell is located at the center of the cell body and perceives pressure through compression of the impermeable seal. When the manual valve (2)is open, pressure is transmitted to the sample concomitantly with pump compression. When the manual valve (2)is closed, the automatic piston valve (3)is used for small rise time P-jumps. A barometer located between valves (1) and (2) records the pressure of the system. The temperature of the sample is controlled by a thermal bath (colored in red) linked to the cell body. Excitation of the sample is carried out using a lamp and monochromator (Ex Δ). A monochromator in the emission path (Em Δ) precedes the photomultiplier tubes (PMT) and photon counting electronics module connected to a computer (PC)
1.
The equipment. A standard fluorometer is adapted with an HP setup as described in Fig. 1. In comparison to conventional fluorescence, the light path in HP systems, colored in orange, enters into the cell body in order to excite the sample cell immersed into the pressure-transmitting fluid, colored in green, and the emitted fluorescence is collected at 90°. It is important to limit light loss both in the excitation and emission path. Consequently, the pressure-transmitting fluid, usually water, ethanol, or isopropanol, must be of the highest spectroscopic grade possible to avoid signal interferences (see Note 1) to address possible interference on the fluorescence yield. The pressure-generating fluid must have a low compressibility and an index of refraction close to that of the solution under study. Since we work on aqueous protein solutions, water is the preferred pressure-transducing liquid. However, it can only be used if the high-pressure cell and the pressure lines, pump, and gauge are made of stainless steel. Excitation is carried out using a lamp and monochromator coupled to a multimode optical fiber that is focused into the rear window of the sample cell using a lens of appropriate focal length. A detector system is placed at one of the windows of the sample cell that is at 90° to the excitation window. This limits detection of scattered exciting light. Nonetheless, since the inside of the cell is made of stainless steel, scattered light cannot be entirely eliminated. For some applications (in the presence of scattering molecules such as micelles for example), a cut-on filter is placed directly after the emission collection lens. There is also a monochromator in the detection path and the light is focused onto the entrance slit using a lens of appropriate focal length. The detectors used are generally photomultiplier tubes, operating in photon counting mode. The digital output of the PMT is sent to a photon counting electronics module for discrimination and amplification prior to being sent to an interface card in a PC. The hardware used in our system is from ISS Inc (Champaign, IL, USA).
2.
The sample cell. The sample cell is located in the center of the cell body and surrounded by pressure-transmitting fluid. Commercially available cuvettes adapted to a rigid Teflon stopper (ISS, Champaign, IL, USA) and artisanal cuvettes adapted to an impermeable seal with an o-ring will properly transmit pressure to the sample by compression. We address loading issues in Note 2. The sample cell as well as the cell body structural design vary according to the setup and have been described with different degrees of detail elsewhere [8, 23, 29, 57, 73–76, 92].
3.
The high-pressure cell. The high-pressure cell used in our setup is made of heavy stainless steel alloy and was designed in-house and built by SOFOP, La Broussine, Olemps, France [93]. The temperature of the sample is controlled through a thermostat circulating water bath externally coupled to the cell body. The stainless steel cell body acts as a good-temperature buffer, but thermal equilibration is slow. As volumetric properties are sensitive to temperature thermal control must be ensured; see Note 3. The cell is equipped with three sapphire windows, one for excitation, one for emission, and one for transmission (used in optical alignment). The use of sapphire windows precludes fluorescence anisotropy measurements, which require fused silica quartz windows, because sapphire is naturally birefringent. However, quartz is not as pressure resistant as sapphire, and we have found it more advantageous to use the sapphire. The sample cell is loaded through an opening in the top of the cell, and the pressure line is connected in place of the fourth window on the side of the vessel. We have found it very useful to separate the sample loading input from the pressure input, which then is almost never disconnected. This greatly reduces issues of leaks at the seals between the line and the plug.
4.
Manual pump. Pressure is induced by either a manual or a motorized pump acting on the transmitting fluid through a piston and monitored via a pressure gauge. The pump in our system was purchased from SITEC, Hi-Pro Pressure Products Ltd., Aylesbury, England. The HP pump will be more resistant at elevated pressures (>2 kbar); thus if the pump strength is the same, the time to increase pressure will be longer. A compressed air-controlled piston valve (Autoclave France, Nogent-sur-Oise, France) is inserted into the system to allow rapid and kinetically identical pressure rise. The manual pump is increased to the desired pressure with the valve closed and then the pressure increment to the sample cell can be triggered with dead times of ~1 s. Care must be taken while incrementing pressure in order to avoid thermal fluctuations; see Note 4. It is important to include valves to isolate each component of the system in order to identify the sources of eventual leaks.
5.
Buffer. Under HP, the choice of the sample buffer is limited. Even buffers from the Good’s list [94] can be bad pH controllers [95]. Electrostriction of solvent around charges is accompanied by a decrease in volume. Hence, it is key to use buffer systems in which the unprotonated and protonated forms carry the same number of charges and/or small ionization volume [61, 96]. In particular care must be taken to avoid buffers of high ionization volume such as phosphate buffer essential. For example the following buffers are suitable for HP measurements: CAPS for pH range 9.5–11.5, Tris–HCl for pH range 7–9, MES or Bis-Tris for pH range 5.5–7.5, and sodium acetate for pH range 3.8–5.8. Once the buffer is defined, combinations with other additives have been widely implemented (see Note 5).
6.
Fluorophores. The quality of the sample, i.e., purity and solubility, is crucial to avoid contaminating fluorescence, scattering, or other signal distortions. Recombinant or purchased polypeptides must be at least 95 % pure; mass spectrometry or polyacrylamide gels can be used to ensure the purity of the sample. The presence, quantity, and position (if structure is known) of intrinsic fluorescent residues must be known. The same information must be known if extrinsic covalently bonded fluorophores are used, e.g., FITC or other organic dyes. Often, the intrinsic stability of a protein or a complex and/or a small difference in volume can preclude the study of the desired phenomenon (unfolding, dissociation, etc.). In these cases, one can use stabilizing or destabilizing additives such as osmolytes or chemical denaturants or an acid or a base, as needed to “tune” the transition into the available pressure window. In such cases, care must be taken to use highly pure additives as well. Moreover, as presented below volumetric properties on proteins are sensitive to the presence of internal void volumes; additional information of the protein sample like cavity density and distribution as well as global stability may also be valuable before starting an HP experiment; see Note 6.
3 Methods
3.1 Equilibrium Unfolding
As described in the previous section and in comparison with atmospheric fluorescence experiments, the time required for cell loading, thermal equilibration, and equipment maintenance complicates but does not preclude the performance of titration experiments (see Note 7). For that reason we chose to describe a simple unfolding study on SNase protein (Fig. 2) that can be extrapolated to other experimental approaches. The high quantum yield and solvatochromic properties of tryptophan residue allow monitoring accurately the folded and unfolded states of proteins [72]. The protein intrinsic fluorophore signal can be followed in function of pressure by observing the following:
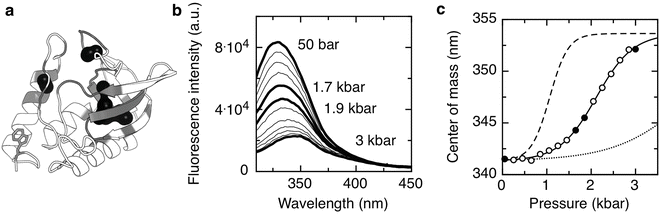

Fig. 2
Equilibrium HP unfolding of SNase protein. (a) Cartoon representation of the crystallographic structure of SNase (PDB ID 1SNC), the single tryptophan residue is represented with sticks, the molecular surface of cavities is represented in black-filled circles, and residues surrounding cavities are colored in grey. (b) Fluorescence emission spectra of SNase protein carried out at different pressures. The initial and the final emission spectra as well as the spectra at 1.7 and 1.9 kbar are highlighted in black. (c) Center of spectral mass calculated from the emission spectra recorded at different pressures. Solid line corresponds to data fitted to a two-state unfolding model and leads to a ΔG of 2.9 ± 0.1 kcal/mol and a ΔV of 60 ± 6 ml/mol. Dashed and dotted lines correspond to simulations of a two-state unfolding model by only changing ΔV to 120 or 30 ml/mol, respectively. Filled circles correspond to highlighted spectra of (b). Cavities were calculated using HOLLOW [139] and represented using PyMOL [148]. Unfolding was carried out at 10 mM Bis-Tris pH 5.5 at 20 °C, protein concentration of 50 μM, and excitation wavelength of 290 nm
1.
2.
3.
Anisotropy: Upon unfolding the anisotropy value decreases due to an increment of rotational mobility [72]. Note that this is only possible if the windows of the high-pressure cell are in quartz, and even then correction factors must be determined and applied to correct for pressure-induced birefringence in the quartz windows [92, 99]; see Note 8.
In Fig. 2b we show the spectra of emission of SNase protein as function of pressure. The equilibration times after each pressure increment must be complete and well defined (see Note 9). In Fig. 2c we plot the center of spectral mass of the emission spectra, an accurate method to quantify spectral shifts [31, 32]:
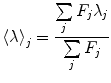
with F j fluorescence intensity at wavelength λ j = 320, 321, 322, …, 450 nm. One can also do the computation in terms of energy (cm−1). The center of spectral mass provides data of higher quality because it is an integral value, as opposed to the intensity at an individual wavelength. For each pressure-induced unfolding measurement, the center of spectral mass was fitted as a function of pressure for values of ΔG o u and ΔV o u taking into account the correction by the relative quantum yield of unfolded and folded states obtained from the ratio of the high- and low-pressure spectra. For pressure-induced equilibrium unfolding analysis, the free energy of unfolding is assumed to evolve linearly with the pressure, p:
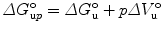
where
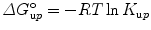
and
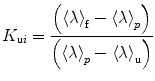
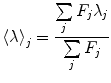
(2)
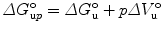
(3)
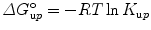
(4)
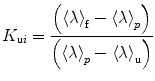
(5)
To account for differences in quantum yield between the folded and unfolded state in calculating the observable from the free energy for the nonlinear least squares fit, we assume that the observable (<λ> p ) at pressure p is a linear weighted sum of the observable value for F and U (<λ>f and <λ>u), weighted for both their fractional population at that pressure, α i,p (obtained from the value of free energy), and their fractional quantum yield calculated, f Q :
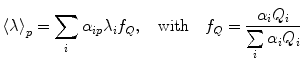
where Q is the normalized quantum yield of species, i (in this case there are only two species, F and U). For deconvolution details refer to [23, 25, 63, 69, 73–77]. Relative to the partial molar volume of a folded protein (volume/mole), the magnitude of the partial molar volume decrease upon unfolding ΔV o is rather small, approximately two orders lower, and in the range of 50−150 ml/mol or 0.5–2 % of the total [23, 25, 63, 69, 73–75]. Nonetheless, these small differences of volumes, ΔV o > 5 ml/mol, can be detected in pressure experiments, since the pressures used are rather high (2–4 kbar). As extensively demonstrated by the effect of cavity creating mutants on the hyperstable variant SNase, Δ + PHS [87], but also perceived earlier on T4 lysozyme [58] and other proteins [71, 82, 100–102], picturing the tridimensional location of cavities (Fig. 2a) can be helpful for data interpretation (refer also to Note 6). The larger the amount of solvent-excluded volume in the folded state which is eliminated in the unfolded state, the higher the absolute value of the volume change of unfolding, ΔV o, sharpening the curves, as simulated in Fig. 2c. Temperature modulates significantly the magnitude of ΔV o because the thermal expansivity of folded states is much smaller than that of unfolded states (refer to Note 3). This phenomenon, along with the ΔC p of protein folding, is largely responsible for ellipticity and tilt of protein folding pressure–temperature-phase diagrams [46], and can lead to a change in sign of the volume change at high temperature [103].
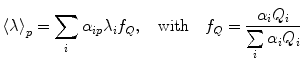
(6)
3.2 Relaxation Kinetics
It is of interest to use pressure jump relaxation to investigate the volumetric properties of the TSE for two-state protein folding. In Fig. 3a we describe an example of the 0.2 kbar P-jump from 1.7 to 1.9 kbar of SNase protein. Here we simply monitor the intensity at a given wavelength, as this observable does not need to be quantum yield corrected. Intensity versus time profiles were fitted to a single exponential decay:
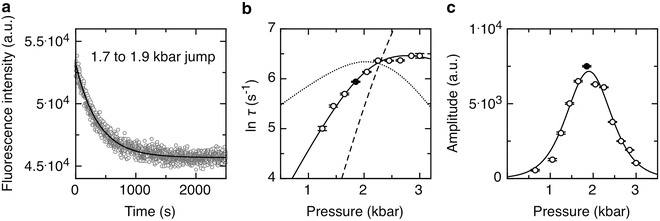
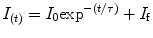
where I 0 is the intensity at time 0 before the jump, τ is the apparent macroscopic relaxation time or the time at which the population of the assembly is reduced to 1/e times its initial value, and I f is the final fluorescence intensity. As revealed by random distribution of residuals, the absolute difference between experimental data and the fitted function, the decay of fluorescence intensity upon incrementing pressure fits well to the single exponential. It is important to ensure the end of the transition (see Note 9).

Fig. 3
HP relaxation kinetics of SNase protein. (a) Fluorescence intensity kinetics of a 0.2 kbar typical P-jump to 1.9 kbar. Solid line corresponds to data fitted to a mono-exponential function, leading to a macroscopic τ of 380 s and an amplitude of fluorescent signal of 7,500 ± 50 a.u. (b) Dependence of the lnτ(s) with pressure. Solid line corresponds to data fitted to a two-state unfolding model and leads to an activation volume of 52 ± 0.1 ml/mol and a k f of 0.077 ± 0.011. Dashed and dotted lines correspond to simulations of the two-state unfolding model by setting the activation volume to 100 or 25 ml/mol, respectively. (c) Dependence of the amplitude with pressure. Solid line corresponds to data fitted to a two-state unfolding model (see text) and leads to a ΔG of 3.1 ± 0.1 kcal/mol, a ΔV of 70 ± 1 ml/mol, and a p 1/2 of 2.00 ± 0.01 kbar in agreement with results presented in Fig. 2. Filled circles correspond to data from the example shown in panel A. P-jumps were carried in between each emission spectrum presented in Fig. 2, the excitation wavelength was 290 nm, and emitted intensity was recorded at 340 nm
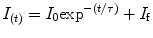
(7)
From the solution of the set of differential equations defining the change in population of the folded and unfolded states after a pressure jump,
![$$ \frac{{\delta [F]}}{{\delta t}}=-{k_{\mathrm{ u}}}[F]\quad \mathrm{ and}\quad \frac{{\delta [U]}}{{\delta t}}=-{k_{\mathrm{ u}}}[U] $$](/wp-content/uploads/2017/03/A299540_1_En_4_Chapter_Equ00048.gif)
we find the eigenvalue
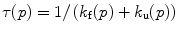
where τ(p) is the relaxation time after a pressure jump to pressure p. This value depends only upon the final pressure, not the direction or the size of the jump, in the limit of relaxation kinetics [104]. In formal analogy with Eq. 1, the dependence of the apparent rate constant τ on the pressure can be derived from the Eyring theory [105] and can be written as
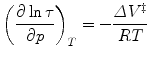
![$$ \frac{{\delta [F]}}{{\delta t}}=-{k_{\mathrm{ u}}}[F]\quad \mathrm{ and}\quad \frac{{\delta [U]}}{{\delta t}}=-{k_{\mathrm{ u}}}[U] $$](/wp-content/uploads/2017/03/A299540_1_En_4_Chapter_Equ00048.gif)
(8)
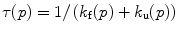
(9)
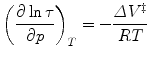
(10)
Plots of the natural logarithm of the relaxation time vs. pressure can be fit for the folding and unfolding rate constants at atmospheric pressure, k f and k u, and the activation volumes for the folding and unfolding reactions, ΔV ‡ f and ΔV ‡ u. The ratio k f/k u corresponds to the equilibrium constant K f, and the sum of the activation volumes, ΔV f ‡ and ΔV u ‡, is equal to the equilibrium volume change of folding ΔV f. The natural logarithm dependence of τ with pressure for SNase, Fig. 3b, presents profiles that are analogous to the chevron plots obtained with chemical denaturants [106, 107], with the exception that the sign of the activation volumes is not necessarily known. For example, denaturant always decreases the folding rate and increases the unfolding rate, although of course this occurs at varying degrees for different proteins. The activation volumes, on the other hand, can both be positive [108]. Hence, the plots do not necessarily present a chevron shape [90]. The basic principles of relaxation kinetics can be found in order to improve the robustness of the fitting, it is suitable to restrict the quantity of parameters to the smallest amount possible; the simpler (as in simpler not simplest) the better [109]. Instead of fitting to four parameters, we restricted to two parameters ΔV ‡ f and k f by constraining the k u and ΔV u ‡ values to the equilibrium constant and volume change [89, 110].
The ratio between ΔV ‡ and ΔV, or V TSE-value [111], informs about the volumetric properties of the TSE relative to the folded and unfolded states. As simulated in Fig. 3b, the V TSE-value relationship modulates the shape of the inverted chevron-plot. A value of 1 or higher implies that the rate-limiting step of the reaction is rather native-like presenting solvent excluded cavities, as it is the case for the presented data with SNase, observed in different conditions [5, 12, 112]. Volumetrically native-like TSEs have been reported for a number of other proteins [59, 67, 78, 113–117]. On the contrary, a low V-value, < (as in much much less) <1, involves an unfolded like TSE, i.e., the cavities are not formed and this volume occupied by solvent [118]. Moreover, in analogy to the Phi-value analysis [119], the V TSE-value analysis [111] emerges as a tool to provide volumetric information on the effect of mutations on the TSE and thereby the structural properties of the protein at the folding barrier [120].
In Fig. 3c we plot the dependence of relaxation amplitudes with pressure. Relaxation amplitudes were calculated from the monoexponential decays (Fig. 3a). The width of the Gaussian distribution of the relaxation amplitudes reflects the sharpness of the sigmoid of the equilibrium-unfolding curve (Fig. 2c); the maximum amplitude value corresponds to the largest difference between the initial and the final states. In two-state systems, the position near the maximum amplitude (Fig. 3c) corresponds to the pressure unfolding midpoint, analogous to the melting point, i.e., the p 1/2 value. This p 1/2 corresponds to the equilibrium situation where K = 1; thus from Eq. 1 p 1/2 = ΔV/ΔG for simple two-state systems. In some cases as in p-jumps, K and ΔV can be determined from relaxation amplitudes; refer to [90]. We analyzed the dependence of p-jump relaxation amplitudes as described for thermal relaxation amplitudes by the Gruebele laboratory [91] (Fig. 3c). Because amplitude signal focuses on the transition of the reaction, the fit is robust allowing bona fide parameterization of curves with incomplete baseline signal, underlining the usefulness of the method in experiments with low signal/noise in the folded or the unfolded states (see Note 10).
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


