If the results of a study reveal an interesting association between some exposure and a health outcome, there is a natural tendency to assume that it is real. (Note that we are considering whether two things are associated. This does not necessarily imply that one causes the other to occur. We will discuss approaches to determining causality further in Chapter 10.) However, before we can even contemplate this possibility we have to try to rule out other possible explanations for the results. There are three main ‘alternative explanations’ that we have to consider whenever we analyse epidemiological data or read the reports of others, no matter what the study design: namely, could the results be due to
chance,
bias or error, or
confounding?
We will discuss the first of these, chance, in this chapter and will cover bias and confounding in Chapters 7 and 8, respectively.
Random sampling error
When we conduct a study or survey it is rarely possible to include the whole of a population1 so we usually have to rely on a sample of that population and trust that this sample will give us an answer that holds true for the general population. If we select the sample of people wisely so they are truly representative of the target population (the population that we want to study) and, importantly, if most of those selected agree to participate, then we will not introduce any selection bias into the study (we touched on the issue of selection bias in Box 3.2, and will discuss it further in Chapter 7). However, even in the absence of any selection bias, if we were to study several different samples of people from the same population it is unlikely that we would find exactly the same answer each time, and unlikely that any of the answers would be exactly the same as the true population value. This is because each sample we take will include slightly different people and their characteristics will tend to vary from those in other samples – just by chance. This is known as random sampling error.
Imagine that you were interested in the health effects of obesity and wanted to know the average body mass index (BMI) of 10-year-old children in your community. If you weighed and measured just one or two children you would not obtain a very good estimate of the average BMI of all children – but the more children you studied, the better your estimate would be. The same is true if we are looking for the association between an ‘exposure’ and ‘outcome’, for example the relation between BMI and age. If we only survey a small group of 10-year-olds and another small group of 12-year-olds we might find that, just by chance, the 10-year olds are bigger than the 12-year olds, but the larger our study, the better or more precise our estimate of the true association between age and body-size will be. In general, if we select a small sample of a population then our results are more likely to differ from the true population values than if we had selected a larger sample. The best way to reduce sampling error is thus to increase the size of the study sample as far as is practical. Of course, there is always a trade-off between study size and cost. There are ways in which we can calculate how many people we should include in a study to reduce sampling error to an acceptable level. This is known as the power of the study and we will come back to consider this further after we have looked at some ways to assess the amount of random sampling error in a study.
When we conduct a study to evaluate the relationship between an exposure and disease we may see an association or we may not. We then have to use the information from the sample of people in the study to infer whether the exposure and outcome are truly related in the wider population. There are four possible outcomes for any study, as shown in Figure 6.1.
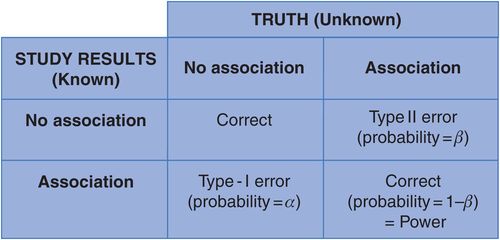
Possible outcomes of an epidemiological study.
If there is really no association between the outcome and exposure then we hope that our study will find just that. Conversely, if the exposure and outcome are truly associated in the population then we want our study to show this association. What we want to minimise are the situations where our study shows an apparent relationship between exposure and outcome when the truth is that there is none (often called a ‘type I’ or alpha error), or our study says there is no association when, in truth, there is (a ‘type II’ or beta error). Unfortunately, in practice we can never know for sure whether we are right or wrong, but we strive to limit this uncertainty by maximising study power (see below) to restrict the role of chance. (We will consider strategies to minimise other types of error in the next two chapters.)
Statistical significance: could an apparent association have arisen by chance?
One way to assess whether an association might have arisen by chance is to carry out what is known as a hypothesis test. This works on a similar principle to many justice systems where someone is presumed innocent until there is sufficient evidence to suggest they are guilty. Here we assume that there is really no association, the ‘null’ hypothesis, unless this is so unlikely to be true that we feel we can reject it in favour of the ‘alternative’ hypothesis that there is a real association. To do this we calculate the probability that we would have seen an association as strong as (or stronger than) the observed association if there were really no difference between the groups (i.e. if the null hypothesis were true). The results of these statistical tests take the form of a p-value (or probability value) and they give us some idea of how likely it is that the groups are truly different and the association is real, or whether the results might just be due to random sampling error or chance (in other words, a type I error, α). For example, if a survey of children shows that girls have a higher average BMI than boys, is this likely to be a true difference or could it just be chance that the girls in the study sample happened to have a higher BMI than the boys?
The null hypothesis (H0) and alternative hypothesis (H1) for a study looking at the relation between drinking coffee and migraine might be:
H0: there is no association between drinking coffee and migraine (i.e. RR = 1.0)
H1: there is an association between drinking coffee and migraine (RR ≠ 1.0).
Imagine that the average BMI of the girls in a survey was 2 units higher than the average BMI of the boys and that statistical testing gave a p-value of 0.01 associated with this difference. We can say from this that, if the average BMIs of boys and girls were in fact the same (i.e. the null hypothesis is true), then we would have only a 0.01 or 1% probability of seeing an apparent difference of 2 units (or more) purely by chance. This is a very low probability, it would occur only 1 in 100 times, thus it seems unlikely to be a chance finding, although it still could be. Conventionally, results are considered to be statistically significant, i.e. unlikely to have arisen by chance, if the p-value is less than 0.05 (p < 0.05); in other words, if the probability that the result would have arisen by chance is less than 5% (i.e. the probability that we are making a type I error, α, is less than 0.05). Using this criterion, we would, therefore, reject the null hypothesis and conclude that the 2-unit difference in BMI between boys and girls was unlikely to have arisen by chance and that, all else being equal, girls probably do have a higher BMI than boys.
Imagine a study which found that, compared with people who exercised regularly, those who did not exercise were three times as likely to have a heart attack (RR = 3.0) and that the p-value for this association was 0.005.
What would the relative risk be if the risk of having a heart attack were the same for people who exercised and those who did not?
How often would we expect to see a relative risk as big as 3.0 if there were really no association?
Is it likely that a study would give a relative risk of 3.0 (p = 0.005) if there were really no association between exercise and heart attack?
If the risk of having a heart attack were the same regardless of how much a person exercised, i.e. there was no association between exercising and having a heart attack, then the relative risk would be 1.0. In the example above the study found a relative risk of 3.0, p = 0.005. The small p-value suggests that it is very unlikely that the study would have given a relative risk as big as 3.0 if the true relative risk were 1.0. (With a p-value of 0.005, we would expect this to happen only about 5 in 1000 or 1 in 200 times.) The observed association between heart attack and exercise is therefore unlikely to have arisen by chance.
Confidence intervals
A hypothesis test is a qualitative assessment of whether or not an observed association is likely to have arisen simply because, by chance, the people who ended up in the study differed in some way from the population norm. A more quantitative way to assess the likely effects of this random sampling error on our estimates is to calculate what is a called a confidence interval around the result. This is in effect an explicit admission that the result of a study,2 often referred to as the ‘point’ or ‘effect’ estimate, is probably not exactly right, but that the real answer is likely to lie somewhere within a given range – the confidence interval. A narrow confidence interval therefore indicates good precision or little random sampling error and, conversely, a wide confidence interval indicates poor precision. The most commonly used confidence intervals are 95% intervals (95% CI) and they are often described slightly inaccurately as meaning that we can be ‘95% confident’ that the real value is within the range covered by the confidence interval. What the confidence interval really means is that if we were to repeat the study many times with different samples of people, then 95% of the 95% confidence intervals we calculated would include the true value. Note that this also means that 5% of the time (or 1 in 20 times) the 95% CI would not include the true value and we will never know which times these are. Other percentages can be used, such as 90%, which gives a narrower confidence interval but less certainty that it will contain the true value (we will be wrong about 1 time in 10); and 99%, which will be more likely to contain the true value (we will only be wrong about 1 time in 100) but will give a wider interval.
To consider a practical example, imagine two studies that have evaluated the association between exposure to air pollution and asthma.
Study 1 finds a relative risk of 1.5 with a 95% confidence interval (CI) of 1.2–1.9.
What does this tell us about the association between air pollution and asthma?
This is a fairly precise estimate. It tells us that people who are exposed to air pollution are about one and a half times as likely (or 50% more likely) to develop asthma than those who are not exposed. It tells us that the risk might be as much as 1.9 times, but also that it might be as little as 1.2 times as high (i.e. a 20% increase) in those who are exposed. It also tells us that the relative risk is unlikely to be more than 1.9 or less than 1.2 (but it still could be outside these values).
Study 2 finds a relative risk of 2.5 (95% CI 0.9–6.9).
What is the most likely value for the relative risk of asthma in people exposed to air pollution in the second study?
Is it possible that the result could have arisen by chance and there is really no association (i.e. the ‘true’ population relative risk is 1.0)?
Which of the two studies would give you most concern that air pollution was associated with asthma?
In the second study, the most likely value for the relative risk is 2.5 and the true relative risk could be as high as 6.9. However, the confidence interval is very wide, indicating poor precision, and it also includes the value 1.0 (remembering that an RR of 1.0 suggests no effect), so it is possible that there is really no association and the result of 2.5 arose by chance. Both results suggest a possible effect of air pollution in inducing asthma. Assuming there is no bias, the first study implies that there is a real association between air pollution and asthma but the effect is not very great. The second study suggests the relative effect might be larger and thus more important clinically, but because of the wide CI we are left with some uncertainty as to how ‘true’ that value really is. We should certainly not ignore the result just because chance is one possible explanation for our findings; after all, the real value is just as likely to be close to 6.0 (a very strong association), as it is to be close to 1.0 (no effect). However, we should be cautious, and acknowledge the possibility that it could merely reflect the play of chance. In practice, if we had to make a judgement about the public health effects of air pollution we would want to consider the results of both studies together to increase the precision of our estimate. We will look at ways to do this in more detail in Chapter 11. For now, it is important to remember that narrow confidence intervals (indicating good precision) are always more informative than wide confidence intervals (indicating poor precision).
See Appendix 7 for some of the most useful formulae for calculating confidence intervals.
The relationship between p-values and confidence intervals
If a 95% CI does not contain the ‘no-effect’ or ‘null’ value then the p-value from a statistical test would be < 0.05. Conversely, if the 95% CI does include the null value then p ≥ 0.05. This means that if both ends of a CI around a relative risk are greater than 1.0 (example (a) in Figure 6.2), it suggests that the positive association between the exposure and outcome is unlikely to be due to chance; similarly if both ends of the CI are less than 1.0, it suggests an inverse association that is unlikely to be due to chance (d). However if the CI includes the null value, i.e. the lower bound is less than 1.0 and the upper bound is greater than 1.0 as shown in examples (b) and (c), then we cannot rule out the possibility that the true relative risk is really 1.0 and thus that there is really no association between the exposure and outcome. In the hypothetical asthma studies above, the 95% CI for study 1 does not include the null value so the corresponding p-value would be less than 0.05 and the result would be termed ‘statistically significant’. The result of study 2, on the other hand, would not be statistically significant because the 95% CI includes the value 1.0 so the p-value would be ≥ 0.05.
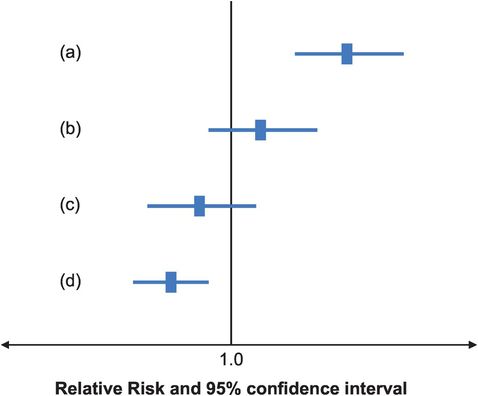
Relative risks and confidence intervals from four hypothetical studies.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


