Chapter 3
Generalised linear mixed models
Up until now, we have considered models with normally distributed errors. However, there are many situations where data are not of this type, for example, where the presence/absence of an adverse event is recorded and the normality assumption cannot be made. A class of models known as generalised linear models (GLMs) is available for fitting fixed effects models to such non-normal data. These models can be further extended to fit mixed models and are then referred to as generalised linear mixed models (GLMMs). Random effects, random coefficients or covariance patterns can be included in a GLMM in much the same way as in normal mixed models, and again either balanced or unbalanced data can be analysed. Although GLMMs can be used to analyse data from any distribution from the exponential family, binary data and Poisson data are most frequently encountered, and for this reason, this book will primarily concentrate on the use of GLMMs for these data types.
In introducing these topics, we will, of necessity, be less than comprehensive. In their excellent book Generalised Linear Models, McCullagh and Nelder (1989) take 500 pages to cover the subject and start by an assumption of ‘a knowledge of matrix theory, including generalised inverses, together with basic ideas of probability theory, including orders of magnitude in probability’. At one end of the readership spectrum, therefore, those with no experience of GLMs may wish to skip all but the introductory paragraphs of each section because some sections inevitably draw on the assumption of prior knowledge. This will enable such readers to identify where such methods might prove useful. In case the reader with little background knowledge of GLMs identifies a need to apply GLMs and GLMMs and is horrified at the prospect of having to master textbooks on the subject, we would emphasise that fitting such models can often be achieved without an encyclopaedic knowledge of the topic. The final section of this chapter and sections of subsequent chapters will illustrate the application of these models and present the SAS code needed to implement them.
We will start by describing the GLM in Section 3.1 and then show how it is extended to the GLMM in Section 3.2. GLMMs are more complex than normal mixed models, and there is therefore more potential for problems such as biased estimates and a failure to converge. These are considered in Section 3.3, which also gives some practical information on fitting GLMMs. A worked example is given in Section 3.4.
3.1 Generalised linear models
3.1.1 Introduction
GLMs can be used to fit fixed effects models to certain types of non-normal data: those with a distribution from the exponential family. Consider the following example. We wish to conduct a clinical trial to investigate the effect of a new treatment for epilepsy. A suitable variable for assessing efficacy is the number of seizures that occur during a predetermined period. Thus, the response variable is a count. Such variables are often found to follow a Poisson distribution. This is a member of the exponential family, and GLMs or GLMMs can be considered, depending on the details of how the trial is designed. Such an example is considered in Section 6.4. As a second example, consider the analysis of a particular adverse event in a clinical trial. In some situations, a simple contingency-table-based analysis will be sufficient. If, however, there are baseline effects or if the trial design is more complicated, a GLM may be preferred. In the multi-centre trial, which we are regularly revisiting in this book, the occurrence of cold feet was such an adverse event and could be reported at any of the follow-up visits. As a binary outcome, this is also from the exponential family, and in Section 3.4, we will show how GLMMs can be applied to these data.
As with the models we have met for normally distributed data, the models use a linear combination of variables to ‘predict’ the response. In the case of normally distributed data, the fixed effects model is y = Xα + e. That is, the response is determined by the linear component, Xα, which gives the expected response, which we will denote by μ and by a randomly determined error term. In a somewhat convoluted way, we could write the model as
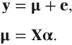
The GLM can easily be specified from this artificial-looking model by allowing μ and Xα to be related by a ‘link function’, g, so that
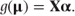
Thus, normal models are a special case of GLMs in which the link function is the identity function. In general, the link function is not the identity function but takes a form suitable for the distribution of the data.
An alternative, less mathematical way of familiarisation with the concept of the GLM is to think of the link function as a method of mapping the response data from their scale of observation to the real scale (−∞, + ∞). For example, binomial probabilities have a range 0–1, and the logit link function, log(μ/(1 − μ)), will translate this range to the real scale. This is necessary because fitting a linear model directly to the binomial parameter could lead to estimates of probabilities that were negative or greater than one. Use of the link function allows the model parameters to be included in the model linearly, just as in the models we have described for normal data. This often gives the GLM an advantage over contingency table methods, which are sometimes used to analyse binary data (e.g. chi-squared tests) because these methods cannot incorporate several fixed effects simultaneously.
In this chapter, we will give only a brief introduction to GLMs. However, more detail can be found in McCullagh and Nelder (1989). Before defining the GLM, basic details of the binomial and Poisson distributions will be given for those who are not completely familiar with these distributions, and the general form for distributions from the exponential family will be specified. This general distributional form will be needed for setting a particular form of link function known as the ‘canonical’ link.
3.1.2 Distributions
We now define the Bernoulli, binomial and Poisson distributions. These can all be described as ‘one-parameter’ distributions, that is using a single parameter completely describes the distribution.
The Bernoulli distribution
This distribution is used to model binary data where observations have one of two possible outcomes, which can be thought of as ‘success’ or ‘failure’. If one is used to denote success and zero failure, the density function is
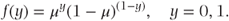
Thus, μ corresponds to the probability of success, and the mean and variance are given by
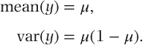
The binomial distribution
This distribution is also suitable for binary data. However, observations are now recorded as the number of successes out of a number of ‘tries’. The parameter of interest is the proportion of successes. If z and n are the observed numbers of successes and tries, respectively, then the proportion y = z/n has a density function
and
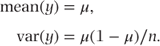
Note that when n = 1, the Bernoulli density function is obtained. Thus, the Bernoulli distribution is a special case of the binomial distribution.
The Poisson distribution
This distribution can be used to model ‘count’ data. The number of episodes of dizziness over a fixed period and the number of abnormal heart beats on an ECG tape of a prescribed length are examples of count data. Its density function is given as
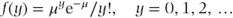
and
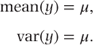
The Poisson distribution with offset
Sometimes, the underlying scale for count data varies with each observation. For example, observations may be made over varying periods (e.g. number of epileptic seizures measured over different numbers of days for each patient). Alternatively, the underlying scale may relate to some other factor such as the size of a geographical region over which counts of subjects with a specific disease are taken. To take account of such a varying scale, the scale for each observation needs to be utilised in forming the distribution density. The scale variable is often referred to as the offset. The parameter of interest is then the number of counts per unit scale of the offset variable. If we denote the offset variable by t (even though it is not always time) and the observed number of counts by z, the distribution of y = z/t has a density function
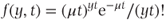
and
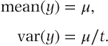
Note that when t = 1, the density function for the Poisson distribution without an offset variable as shown previously is obtained, confirming it as a special case of this distribution.
3.1.3 The general form for exponential distributions
To show how the GLM can be used for data with any exponential family distribution, we first need to define a general form in which all exponential family density functions can be expressed. This can be written as
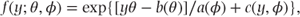
where
- θ = a location parameter (not necessarily the mean),
- φ = a dispersion parameter (only appears in distributions that have two parameters such as the normal distribution).
The form of the functions a, b and c will be different for each distribution. Distributions that are not from the exponential family cannot be expressed in this way.
The one-parameter distributions considered in this book can be defined solely in terms of the location parameter, θ, and the general form then simplifies to
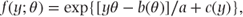
where a is now a constant. Expressions for a, b(θ) and c(y) are listed in the following table for the Bernoulli, binomial and Poisson distributions:
| Distribution | a | b(θ) | c(y) |
| Bernoulli | 1 | log(1 + exp(θ)) | 1 |
| Binomial | 1/n | log(1 + exp(θ)) | log[n !/((ny) ! (n − ny) !)] |
| Poisson | 1 | exp(θ) | − log(y !) |
| Poisson with offset | 1/t | exp(θ) | yt log(yt) − log(yt !) |
where n and t are the denominator and offset terms, respectively. Details of exactly how these expressions are obtained from their density functions will be given later in Section 3.1.6.
It can be shown that the mean and variance of a distribution can then be written in terms of the functions a and b as
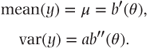
Hence, θ = b′− 1(μ), and we can alternatively write the variance in terms of μ as
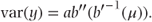
Using these expressions, the means and variances for the distributions can then be written in terms of θ or μ as follows:
| Distribution | Mean μ = b′(θ) | Variance in terms of θ, ab″(θ) | Variance in terms of μ |
| Bernoulli | (1 + exp(−θ))− 1 | exp(θ)/(1 + exp(θ))2 | μ(1 − μ) |
| Binomial | (1 + exp(−θ))− 1 | exp(θ)/(1 + exp(θ))2/n | μ(1 − μ)/n |
| Poisson | exp(θ) | exp(θ) | μ |
| Poisson with offset | exp(θ) | exp(θ)/t | μ/t |
3.1.4 The GLM definition
In Section 3.1.1, we defined the GLM using the matrix notation used for normal models by
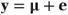
and related μ to a linear sum of the fixed effects, Xα (the linear component), by a ‘link function’, g, so that
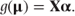
To relate the GLM directly to the general exponential density function introduced in the previous section, we label the linear component θ so that θ = Xα. We will next consider how link functions can be constructed.
Canonical link functions
A type of link function known as the canonical link function is given by
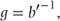
where b is obtained from the general form for the density function for exponential distributions given previously. For the distributions we have considered, the canonical link functions are given by
| Distribution | g(μ) = b′− 1(μ) | Name |
| Bernoulli | log(μ/(1 − μ)) | Logit |
| Binomial | log(μ/(1 − μ)) | Logit |
| Poisson | log(μ) | Log |
| Poisson with offset | log(μ) | Log |
In most situations, use of the canonical link function will lead to a satisfactory analysis model. However, we should also mention that there is not a strict requirement for canonical link functions to be used in the GLM, and non-canonical link functions are also available. These are not derived from the density function but still map the data from their original scale onto the real scale. For example, a link function known as the probit function, g(μ) = Φ− 1(μ) (where Φ is the cumulative normal density function), is sometimes used for binary data recorded in toxicology experiments, since values of μ corresponding to specific probabilities can easily be obtained using the normal density function. Despite not being canonical, this link function does still map the original range of the data (0 to 1) to − ∞ to ∞ as required for the GLM. In this book, we will not be considering non-canonical link functions. However, further information can be found in McCullagh and Nelder (1989).
We earlier specified a general formula for the variance in the GLM as var(y) = ab″(θ). Using the relationship g = b′− 1, for canonical link functions, we can now equivalently write the variance in terms of μ and the function g as
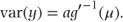
The variance matrix, V
The variance matrix for the GLM may be written as
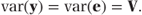
Since the GLM is a fixed effects model, the observations are assumed to be uncorrelated, and the variance matrix, V, is therefore diagonal. The diagonal terms of this matrix are equal to the variances of each observation given the underlying distribution. So, for example, in an analysis of six Bernoulli observations, where μ = (μ1, μ2, …, μ6)′, V can be written as
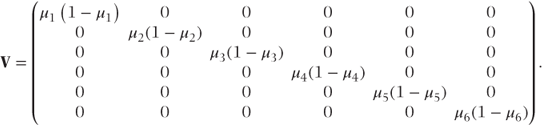
Note that unlike the fixed effects model for normal data, the variances are different for each observation.
In the previous subsection, we showed that the variance could be written in the general form
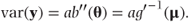
We can use a and b″(θ) to express V in matrix form as a product of two diagonal matrices:
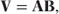
where
- A = diag{ai},
- B = diag{b″(θi)} = diag{g′− 1(μi)}.
For the binomial distribution, A is a diagonal matrix of inverses of the denominator terms (number of ‘tries’). For example, for a dataset with six observations, A would be
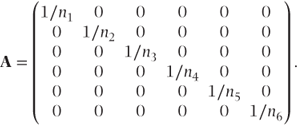
For a Poisson distribution with offset, the ni are replaced by the offset variable values, ti.
B is a diagonal matrix of variance terms. For the Bernoulli and binomial distributions, it is
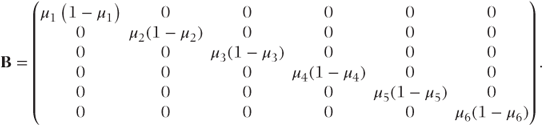
Note that for the Bernoulli and Poisson distributions, ai = 1 and thus A = I (the identity matrix) and V = B.
The dispersion parameter
Variance in the model can be increased (or decreased) from the observation variances specified by the underlying distribution (i.e. aib″(θi)), by multiplying the variance matrix by a dispersion parameter, φ:
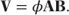
An alternative dispersion parameter is suggested by Williams (1982) for binary data. In this case, φi is calculated using a formula that varies depending on the denominator of each observation and so adjusts for their differing variances:
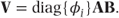
It is referred to as the ‘Williams modification’. Before GLMMs were developed, dispersion parameters were frequently used as a limited facility to model variance at the residual level in one-parameter distributions. We will consider the implications of using a dispersion parameter further in Section 3.3.7.
3.1.5 Fitting the GLM
For readers who wish to understand the ‘mechanics’ of how the GLM is fitted, we now look at the numerical procedures involved.
The GLM is fitted by maximising the log likelihood function. Using the general form for a one-parameter exponential distribution given in Section 3.1.3:
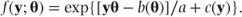
The log likelihood for a set of observations can be written as
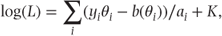
or, in matrix/vector notation, as
where
- θ =
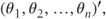
- b(θ) =
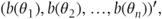
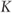= constant.
In fixed effects models for normal data, we saw that a solution for α was easily obtained by differentiating the log likelihood with respect to α and setting the resulting expression to zero (Section 2.2.2). However, in GLMs, the differentiated log likelihood, d log(L)/dα, is non-linear in α, and an expression giving a direct solution for α cannot be formed. To obtain d log(L)/dα, we differentiate log(L) (A) after substituting θ = Xα:
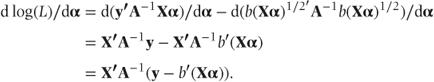
Setting this differential to zero leads to equations that can, in principle, be solved for α. However, because they are non-linear in α, one of the approaches below is usually used instead to obtain estimates of α.
The likelihood function can be maximised directly for α using an iterative procedure such as Newton–Raphson (see Section 2.2.4). The variance of the resulting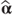 
can be calculated at the final iteration by (from McCullagh and Nelder, [1989], Chapter 9)
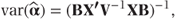
where
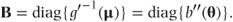
We see that B is a diagonal matrix containing the variances of the individual observations.
Alternatively, the likelihood can be maximised using an iterative weighted least squares method. This approach (defined by McCullagh and Nelder, [1989], Section 2.5) can be based on analysing the following pseudo variable, z, which can be thought of as a linearised observation vector:
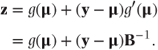
z can, in fact, be defined as a first-order Taylor series expansion for g(y) about μ.
Recalling that g(μ) = Xα, we see that z has variance
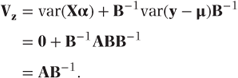
A normal model can then be expressed in terms of the linearised pseudo variable, z:
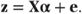
z is then analysed iteratively using weighted least squares (see Section 2.2.1). Weights are taken as the inverse of the variance matrix Vz. Iteration is required because z and Vz are dependent on α. The raw data, y, can be taken as initial values for z. Alternatively, g(y) can be used for the initial values, although an adjustment may be necessary to prevent infinite values. The identity matrix can be used initially for Vz. The initial fixed effects solution is calculated using these values of z and Vz as
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
