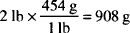
The traveler can go to the butcher and ask for 900 grams of beef to get approximately the 2 pounds needed.
Computations involving units will always require some knowledge of different systems of measurement and intersystem conversions (Chapter 2 and Appendix 1)
Perform the operations indicated:
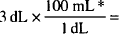
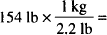
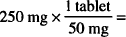
Solutions.
Solution. 16 fluidounces
CALCULATIONS
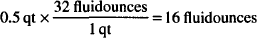
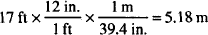
The first fraction converts feet to inches; the second converts inches to meters. Notice that all units except for meters cancel out There is no change in the value of the length represented by “17 ft.” This technique may be extended to any number of successive conversions.
How many fluidounces are there in 1.75 liters (L)? (1L = 1000 mL; 1 fluidounce = 29.6 mL)
Solution. 59.1 fluidounces
CALCULATIONS
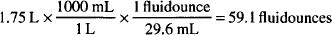
Solution. 1.01 atm
CALCULATIONS
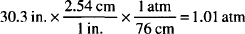
DIMENSIONAL ANALYSIS
A clear view of this method is shown through the following example.
A pharmacist wants to know how many inhalers should be dispensed to a patient to provide a 60 day supply of beclomethasone. The recommended dose is 168 μg twice daily. The commercial inhaler delivers 42 μg per metered dose and contains 200 inhalations.
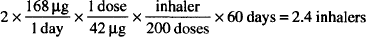
Thus, 3 inhalers must be dispensed.
Now, try to do the next problem using dimensional analysis.
A drug is administered as a single daily dose of 10 mg/kg. How many milliliters of a 10 mL vial containing 100 mg per milliliter would be administered to a patient weighing 154 lb? (1 kg = 2.2 lb)
Solution. 7 milliliters
CALCULATIONS
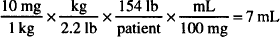
Solutions.
RATIO
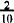, and would be read as 2 to 10.Because a ratio is a quotient, it is regulated by the same rules used for common fractions, for example:
The two terms may be multiplied or divided by the same number, e.g., the ratio 2 : 10 (or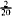 
) will not change if both terms are multiplied by 2. The ratio will become 4:20 or 
.
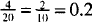Two ratios with the same value and their cross products are equivalent, e.g.,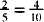 
and 2 × 10 = 5 × 4.
PROPORTION
Try to solve the following problems, using proportion, before verifying your answers.
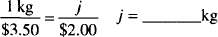
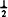lb? (1 lb = 16 oz)
Solutions.
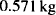
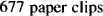
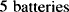
Proportions are useful in those situations where two properties are directly related to each other. For example, if a drug costs 5¢ per gram, 2 g will cost 10¢. The two properties, cost and amount of drug, are directly related to each other. If the quantity of drug is increased five times, the cost will increase five times. If the amount of drug is cut in half, the cost will be halved also. If we wanted to know the cost of 12.5 g of this drug, we could write
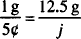
This equation states, “If 1 g of a drug costs 5¢, then 12.5 g will cost j.” Notice that the same units are found on both sides of the equality. The ratio on the left describes the known relationship between the related properties. The ratio on the right describes the unknown situation. The two ratios are equal to each other because there is a fixed relationship between cost and weight.
One sodium bicarbonate tablet contains 300 mg of the drug; we wish to find the number of tablets that will contain 1500 mg of sodium bicarbonate. Which of the following proportions will lead to the correct solution? Why are the others not correct?
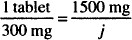
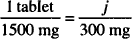
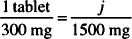
Solution. C is correct. The ratio on the left describes the known information; that on the right, the unknown situation. Both ratios have the same units. A is incorrect because the same units do not appear in both sides of the equality (tablets/mg do not equal mg/tablet). B is incorrect because the first ratio states that 1500 mg are found in each tablet (1500 mg and 300 mg are reversed). Although the units appear to be correct, the numbers have been jumbled.
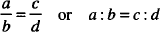
we make use of the fact that the product of the first and last terms or the extremes (a and d) is equal to that of the two central terms or the means (b and c). That is, a × d = c × b. To return to our problem,
A formula for 42 capsules (caps) calls for 300 mg of a drug. Using proportion, find how many milligrams of the drug would be needed to make 24 capsules.
Solution. 171 mg
CALCULATIONS
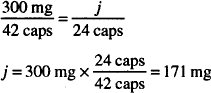
Solution. 87.5 mL
CALCULATIONS
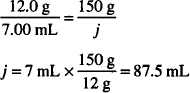
Solution. 9.14 kg
CALCULATIONS
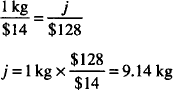
ESTIMATION: ROUNDING AND POWER-OF-10 NOTATION
One kind of check is particularly useful in preventing errors of large magnitude such as misplacement of the decimal point. The method to which we are referring is mat of estimation, using rounded values. The first step in this process is to round all values to one figure. The figure is kept as it appears in the original number if the figure following it is 4 or less. The single figure is promoted to the next higher number if it is followed by a 5 or higher number. For example,
4.27 rounded to one figure is 4
0.37 rounded to one figure is 0.4
3508 rounded to one figure is 4000
0.00949 rounded to one figure is 0.009
Round the following to one figure:
Solutions.
A formula for 42 capsules calls for 180 mg of sucrose. To estimate the amount of sucrose per capsule, round 42 capsules to 40 capsules and 180 mg to 200 mg:
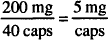
(The exact answer is 4.28 mg per capsule.)
A certain tablet contains 32.5 mg of phenobarbital. Estimate the number of milligrams of phenobarbital in 24 tablets.
Solution. 600 mg
CALCULATIONS
The exact answer is 780 mg. You may think that 600 mg is rather a poor estimate, but it is good enough to tell you that your answer is in the ballpark. Certainly, if you were to solve the problem and come up with an answer of 78 mg or 7800 mg, you would realize that an error had been made.
Solution. $1200.
CALCULAITONS
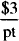× 400 pt = $1200. (The exact answer is $1366.86.)
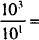
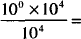
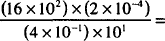
Solutions.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
