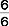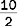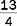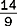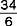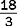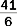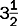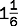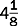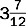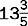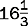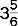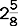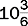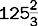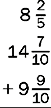General Mathematics
Objectives
• Add, subtract, multiply, and divide fractions and mixed numbers.
• Convert improper fractions and mixed numbers.
• Reduce fractions to lowest terms.
• Create equivalent fractions and compare values.
• Add, subtract, multiply, and divide decimals.
Introduction
This chapter provides a thorough and easy-to-follow review of the arithmetic needed for accurate medication dose calculations. Many examples, practice problems, and answers related to fractions, decimals, rounding, and percentages are offered. Your ability to avoid medication errors and solve medication dose-related problems starts with competence in basic arithmetic. If you need further review, refer to a general basic mathematics text. Mastery of these concepts is essential before you proceed to the following chapters and medication-related calculations.
Fractions
A fraction is part of a whole number. The fraction  means that there are 8 parts to the whole number (bottom number, or denominator), but you want to measure only 6 of those parts (top number, or numerator).
means that there are 8 parts to the whole number (bottom number, or denominator), but you want to measure only 6 of those parts (top number, or numerator).
The fraction 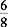 can be reduced by dividing both the numbers by 2.
can be reduced by dividing both the numbers by 2.
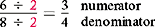
Changing Improper Fractions to Whole or Mixed Numbers
An improper fraction has a numerator that is larger than the denominator, as in.
Examples
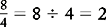 | This is a whole number. |
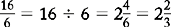 | This is a mixed number because it has a whole number plus a fraction. |
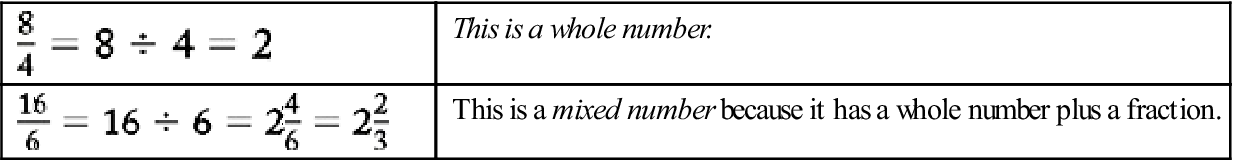
Change the following to whole numbers or mixed fractions and reduce to lowest terms.
Changing Mixed Numbers to Improper Fractions
Examples
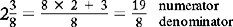
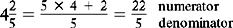
Change the following to improper fractions.
Finding a Common Denominator for Two or More Fractions
To add and subtract fractions, the denominators must be the same.
Example
Fractions with same denominators
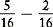 or
or 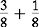 or
or 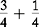
These fractions can be added and subtracted. Each set’s value is also easier to compare because of the common denominators.
Example
Different denominators in fractions with the same value as the fractions in example A:
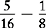 or
or 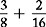 or
or 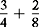
These fractions cannot be added or subtracted until they are converted to equivalent fractions with a common denominator. The relative value of each set is harder to compare until they are converted to equivalent fractions. A common denominator is a number that can be divided evenly by all the denominators in the problem. It is easier to add or subtract fractions if the lowest common denominator is used.
Example
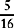 and
and 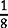 : the largest denominator, 16, can be divided by 8 without a remainder. 16 is the common denominator.
: the largest denominator, 16, can be divided by 8 without a remainder. 16 is the common denominator.
Example
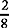 and
and 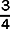 and
and 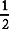 and : the largest denominator, 8, can be divided by 4 and by 2 without a remainder. 8 is the common denominator.
and : the largest denominator, 8, can be divided by 4 and by 2 without a remainder. 8 is the common denominator.
Example
 and
and 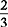 and
and 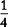 : 3 will not divide evenly into 8.
: 3 will not divide evenly into 8.
The largest denominator. in the group is 8.
8 × 2 = 16 3 will not divide evenly into 16.
8 × 3 = 24 Both 3 and 4 will divide evenly into 24.
8 × 4 = 32 3 will not divide evenly into 32.
8 × 5 = 40 3 will not divide evenly into 40.
8 × 6 = 48 Both 3 and 4 will divide evenly into 48.
Therefore 24 and 48 are common denominators for  and
and  and
and  , but 24 is the lowest common denominator for the three numbers.
, but 24 is the lowest common denominator for the three numbers.
Example
 ,
,  , and
, and 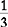
3 and 6 will not divide evenly into 7.
Multiples of 7: 14, 21, 28, 35, and 42.
42 is the lowest number that can be divided evenly by 6 and 3. Therefore 42 is a common denominator, the lowest common denominator.
Changing Fractions to Equivalent Fractions
RULE
Whatever you do to the denominator (multiply or divide by a number), you must do the same to the numerator so that the value does not change.
To maintain equivalence, the numerator and the denominator must be divided (or multiplied) by the same number.
Example
 ,
,  , and
, and 
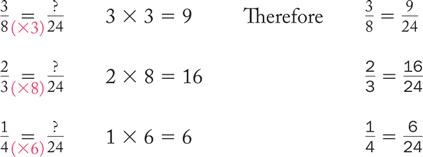
Reducing Fractions to Lowest Terms
A fraction is in lowest terms when the numerator and denominator cannot be divided by any other number except one.
RULE
To reduce a fraction to lowest terms, divide the numerator and denominator by the largest same whole number that will divide evenly into both. When there are no whole numbers that can be used except one, the fraction is in lowest terms.
The fraction  is not in lowest terms because it can be reduced by dividing both the numerator and the denominator by 2, a common denominator.
is not in lowest terms because it can be reduced by dividing both the numerator and the denominator by 2, a common denominator.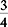 is expressed in lowest terms.
is expressed in lowest terms.
Example
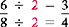
Note that both 6 and 8 are divided by 2.
Example
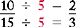
Note that both 10 and 15 are divided by 5.
Example
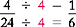
Note that both 4 and 24 are divided by 4.
 and
and  and
and 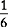 cannot be further reduced. No other number than one will divide evenly into both the numerator and denominator. They are now in their simplest or lowest terms.
cannot be further reduced. No other number than one will divide evenly into both the numerator and denominator. They are now in their simplest or lowest terms.
Changing to Equivalent Fractions Using Higher Terms
RULE
To change a fraction to higher terms and maintain equivalence, multiply both the numerator and the denominator by the same number.
Example
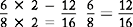
The value has not changed because the multiplier 2 is used for both the numerator and the denominator, and  = 1.
= 1.
Multiplying or dividing numbers by one does not change the value. Equivalence is maintained.
Addition of Fractions and Mixed Numbers
RULE
If fractions have the same denominator, add the numerators, write over the denominator, and reduce.
Example
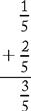
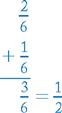
RULE
If fractions have different denominators, convert each fraction to an equivalent fraction using the lowest common denominator and then add the numerators.
Example
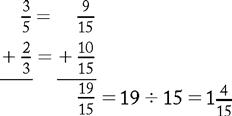
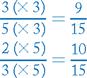
RULE
To add mixed numbers, first add the fractions by converting to a common denominator and then add this to the sum of the whole numbers.
Example
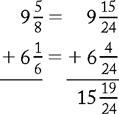
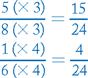
Add the following fractions and mixed numbers, using the common denominator, and reduce to lowest terms.
1. 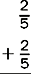
2. 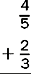
3. 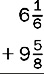
4. 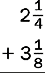
5. 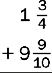
6. 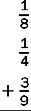
7. 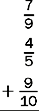
8. 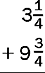
10. 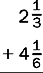
Subtraction of Fractions and Mixed Numbers
RULE
If fractions have the same denominator, find the difference between the numerators and write it over the common denominator. Reduce the fraction if necessary.
Example
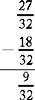
The difference between the numerators (27 minus 18) equals 9. The denominator is 32.
RULE
If fractions have different denominators, find the lowest common denominator and proceed as above.
Example
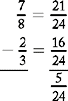
The difference between the numerators (21 minus 16) equals 5. The lowest common denominator is 24.
RULE
To subtract mixed numbers, first subtract the fractions and then find the difference in the whole numbers. If the lower fraction is larger than the upper fraction, you cannot subtract it. You must borrow from the whole number before subtracting the fraction.
Example
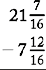
You cannot subtract 12 from 7 because 12 is larger than 7. Therefore you must borrow a whole number (1) from the 21, make a fraction out of 1 (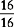 ), and add the 7.
), and add the 7.
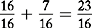
Because you added a whole number to the fraction, you must take a whole number away from 21 and make it 20. The problem is now set up as follows:
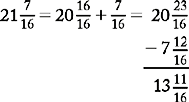
RULE
Reduce your answer to lowest terms.
Subtract fractions and mixed numbers, and reduce the answers to lowest terms.
1. 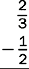
2. 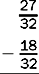
3. 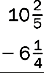
4. 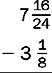
5. 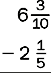
6. 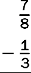
7. 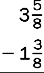
8. 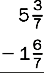
9. 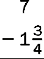
10. 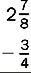
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree