a. Proper fractions have a smaller numerator than denominator.
(1) Example: 5/8
a. Improper fractions have a larger numerator than denominator.
(1) Example: 8/5
b. Reduce improper fractions to mixed numbers.
(1) Example: 8/5 should be reduced to 1 3/5
a. Simple fractions are proper fractions reduced to lowest terms.
(1) Example: 15/24 = 5/8
a. Complex fractions are “fractions of fractions,” where both the numerator and denominator are fractions.
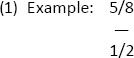
C. Reducing fractions to lowest terms
- To reduce a fraction to lowest terms, divide both the numerator and denominator by the largest multiple common to both terms. The fraction will maintain its value but change its form.
a. Example: 15/24 is reduced to 5/8 by dividing both numerator and denominator by 3: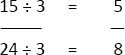
D. Five rules for calculating with fractions
- Understand the impact of multiplying or dividing the numerator and/or denominator by a whole number.
Example: 4/8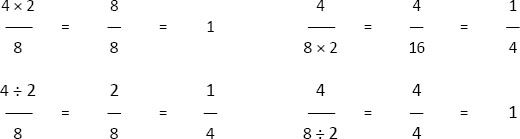
- Convert mixed numbers or whole numbers to improper fractions before performing calculations with other fractions.
a. Example: 2 7/8 = 23/8
- When adding or subtracting fractions, make sure all fractions have a common denominator (i.e., a number into which all denominators may be divided an even number of times).
a. Example: 3/4, 5/8, 1/2 may be written as 6/8, 5/8, 4/8
- Convert answers that are improper fractions back to whole numbers or mixed numbers.
a. Example: 15/3 = 5
- Convert answers to lowest terms
a. Example: 16/32 = 8/16 = 4/8 = 2/4 = 1/2
E. Adding and subtracting fractions
- First convert all fractions to a common denominator. Then add or subtract the numerators.
a. Example: 1/2 + 5/6 + 3/8 = 12/24 + 20/24 + 9/24 = 41/24 = 1 17/24
b. Example: 13/32 – 3/8 = 13/32 – 12/32 = 1/32
F. Multiplying fractions
- Unlike addition and subtraction, multiplying fractions does not require common denominators. Multiply numerators by numerators and denominators by denominators.
a. Example: 9 2/7 × 3/4 = 65/7 × 3/4 = 195/28 = 6 27/28
G. Dividing fractions
- Invert the divisor and multiply the fractions.
a. Example: 11/12 ÷ 1/6 = 11/12 × 6/1 = 66/12 = 5 1/2
b. Example: 10 3/5 ÷ 2 1/10 = 53/5 ÷ 21/10 = 53/5 × 10/21 = 530/105 = 5 5/105 = 5 1/21
II. Decimals
A. Converting decimals to fractions
- Decimal fractions are fractions with denominators of 10 and/or multiples of 10.
a. A decimal number with one digit to the right of the decimal point is expressed in “tenths.”
(1) Example: 0.7 = 7/10
b. A decimal number with two digits to the right of the decimal point is expressed as “hundredths.”
(1) Example: 0.27 = 27/100
c. Follow the same rule as more digits are added to the right of the decimal point.
(1) Example: 0.0365 = 365/10,000
B. Converting fractions to decimals
- To convert common fractions to decimal fractions, divide the numerator by the denominator.
a. Example: 3/4 = 0.75
b. Example: 1 5/8 = 13/8 = 1.625
C. Adding, subtracting, multiplying, and dividing decimals
- When adding, subtracting, multiplying, and dividing decimals and common fractions, convert all terms to the same system before performing the calculation.
a. Example: 25/100 + 1.005 = 0.25 + 1.005 = 1.255
III. Roman Numerals
A. Primary Roman numeral units
SS = 1/2
I or i = 1
V = 5
X = 10
L = 50
C = 100
D = 500
M = 1000
B. Eight rules for using Roman numerals
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


