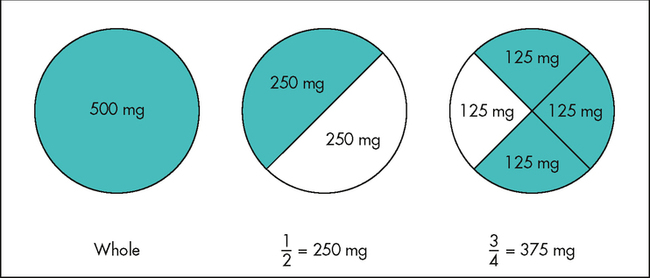
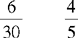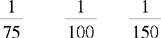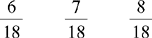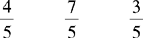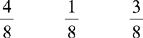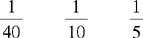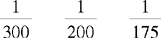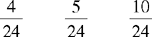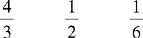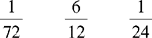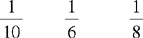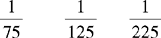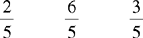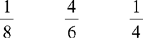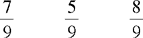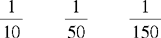CHAPTER 2 Coumadin is an anticoagulant. An overdose of Coumadin (example: 25 mg instead of 2½ mg) can result in a serious adverse effect, such as a severe hemorrhage (Figure 2-1). A fraction is a part of a whole number (Figure 2-2). It is a division of a whole into units or parts (Figure 2-3). Two or more fractions with different denominators can be compared by changing both fractions to fractions with the same denominator (Box 2-1). This is done by finding the lowest common denominator (LCD), or the lowest number evenly divisible by the denominators of the fractions being compared. For the fraction For the fraction Therefore Box 2-2 presents fundamental rules of fractions. BOX 2-2 Fundamental Rules of Fractions In working with fractions, there are some fundamental rules that we need to remember. 1. When the numerator and denominator of a fraction are both multiplied or divided by the same number, the value of the fraction remains unchanged. 2. To change a fraction to its lowest terms, divide its numerator and its denominator by the largest whole number that will divide both evenly.
Fractions
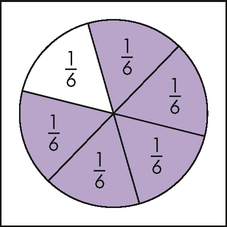
TYPES OF FRACTIONS
Example:
Example:
Solution:
is larger than 
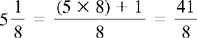
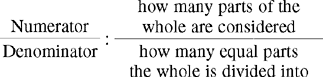
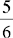
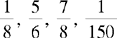
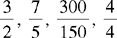
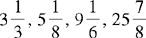
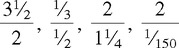
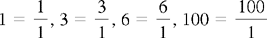
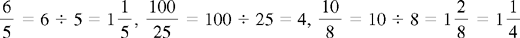
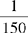
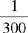
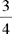
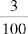
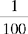
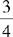
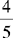
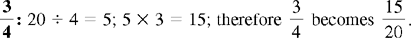
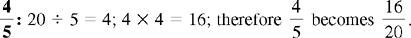
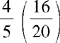
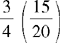
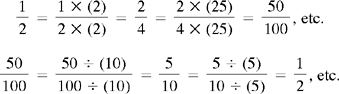
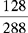
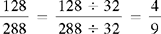
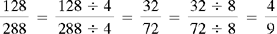
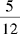
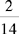
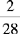
Practice Problems
