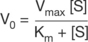chapter 7 Enzymes: catalytic proteins
 The main factors that influence the rate of an enzyme-catalysed reaction are temperature, pH and substrate concentration.
The main factors that influence the rate of an enzyme-catalysed reaction are temperature, pH and substrate concentration.Many of the reactions that make up the metabolic profile of a cell are spontaneous. This means that they can occur without any external energy input. However, the spontaneity of these reactions does not guarantee rapidity. One way to increase the rate of a chemical reaction is to use a catalyst, a substance that speeds up a chemical reaction but which is not consumed in it. Cells use protein-based catalysts called enzymes to speed up cellular reactions that would normally occur spontaneously, but at a much slower rate. Most mammalian cells actually contain many hundreds to several thousand enzymes to give them diverse functionality.
Naming enzymes
Each enzyme has at least two names:
General properties of an enzyme
The general properties of an enzyme are that it:
What slows spontaneous reactions
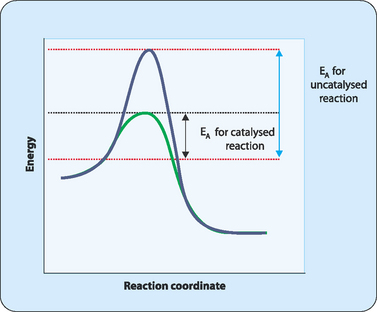
The energy needed to form the unstable intermediate form is called the activation energy (EA) of the reaction (Fig 7-2). A chemical reaction can be envisaged as moving a barrel from one side of a hill to the other. First we have to push the barrel to the top of the hill. In doing this we are putting energy into the system, and this is analogous to the activation energy required by a chemical reaction. At the top of the hill the barrel is now unstable and a small push is all that is required to roll it down to the bottom. This is analogous to the unstable intermediate in a chemical reaction. Once the barrel reaches the bottom of the hill and stops rolling, it has reached a stable state. A similar phenomenon occurs in a chemical reaction. The unstable intermediates transform into products that are more stable molecules.
Lowering activation energy
Cells overcome their prevailing conditions by providing alternative reaction pathways which lower the energy required to convert the substrate (lowered energy of activation) to the unstable intermediate prior to formation of the product. These alternative pathways are provided by enzymes whose active sites provide environments which lower the activation energy for reactions (Fig 7-2). These active sites have multiple functions in that they not only have to carry out catalysis, but also have to recognise specific substrate molecules, and be able to release the product. This means that active sites are actually highly complex molecular machines.
Kinetics of enzyme-catalysed reactions
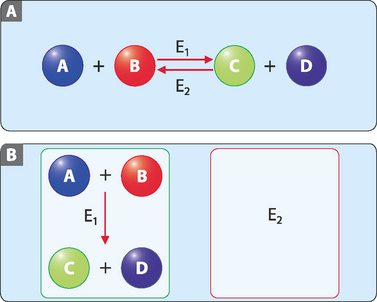
where E = enzyme, S = substrate, ES = enzyme-substrate complex, P = product, and k1, k–1 and k2 are rate constants for the respective reactions.
where V0 = the initial reaction velocity, Vmax = the maximal reaction velocity, Km = the Michaelis constant ((k1 + k2)/k–1) and [S] = the substrate concentration.
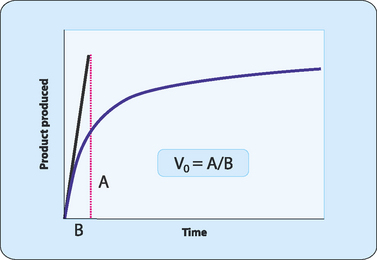
The derivation of the equation required some assumptions to be made. First, it was assumed that there was a large excess of substrate such that the amount of substrate bound to the enzyme at any time is always a small fraction of the total. Next it was assumed that [ES] does not change over time, that it achieves steady state. This means that the researchers assumed that the rate of formation (E + S → ES) was the same as the rate of breakdown (ES → E + P). Finally, they only used the initial velocity of the reaction which was determined in the laboratory as soon as the enzyme and substrate were mixed (Fig 7-3). This ensured that the concentration of product was negligible and that the reverse reaction (P → S) could be ignored.
Km value of an enzyme
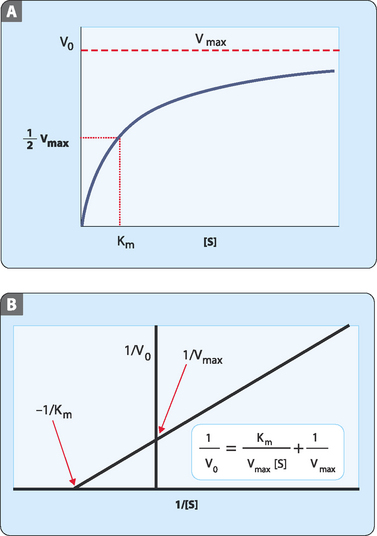
When the initial rate (V0) is plotted against substrate concentration a hyperbolic curve is produced. This makes it difficult to determine an accurate value for Km due to the gradual upward curve at high substrate concentrations (Fig 7-4A). This makes it hard to determine Vmax and hence Km. However, if the data is manipulated to give a straight line it is easier to get determinations of Vmax and Km. One way to do this is to use a double-reciprocal (Lineweaver-Burke) plot in which 1/V0 is plotted against 1/[S] (Fig 7-4B).