New Terminology105
Enzyme Kinetics107
Enzymes as Drug Targets109
Reversible Enzyme Inhibition112
Irreversible Enzyme Inhibition117
Intracellular Effects of Enzyme-Active Drugs120
Summary123
This chapter considers how enzymes can be therapeutic drug targets. The most common therapeutic approach to enzyme control is inhibition; there are four general classes of enzyme inhibition based on the relative affinity of the inhibitor for the enzyme and the enzyme–substrate complex. Competitive inhibition describes inhibitors that have exclusive affinity for the enzyme and compete for substrate binding. Mixed inhibitors bind to the enzyme and the enzyme–substrate complex with different affinity. Non-competitive inhibitors bind equally well to the enzyme and enzyme–substrate complex. Uncompetitive inhibitors bind only to the enzyme–substrate complex. There are special considerations for the blockade of enzymes in cells in that concentrations may differ (from the extracellular medium). In addition, enzyme inhibitors may have no effect until the enzyme is active metabolically under in vivo conditions. Finally, the topic of irreversible enzyme inhibition, enzyme activation and the special cases of drug action on intracellular enzymes is considered.
Keywords
catalysis, competitive inhibition, irreversible inhibition, mixed inhibition, non competitive inhibition, substrate inhibition, suicide inhibitor, tight-binding inhibitor, uncompetitive inhibition.
Introduction
Enzymes are nature’s ubiquitous catalysts mediating thousands of biochemical reactions in the cell to control energy metabolism, oversee macromolecular synthesis and anabolic processes, regulate cell signaling and control cell cycles. Enzymes also control the level of critical molecules in the cell. They do this through accelerating the rate of chemical reactions by lowering the reaction activation energy. Without such catalysts these reactions would progress too slowly to sustain life. For example, without the presence of adenosine deaminase, the removal of the amine from adenosine would take 120 years (as opposed to the rate constant of activation of the enzyme of 370 seconds – an enhancement of 2.1×1012-fold). Hundreds of enzymes control complex biochemical networks (many with strict fidelity to substrate type), although there are notable exceptions to this rule (see Box 6.1). Owing to their obvious key physiological role, enzymes are prime targets for therapeutic drug intervention.
Box 6.1
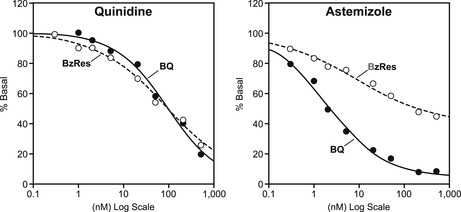
Most enzymes are conservative with respect to the substrate with which they interact so as to preserve signaling and biochemical fidelity in cell pathways. The cytochrome P450 enzymes, however, are designed to be promiscuous since their job is to protect the body from all foreign chemicals. In drug development, drugs are tested as possible inhibitors of cytochrome P450 enzymes as this could cause possible problematic drug–drug interactions. However, the promiscuity and different substrate handling of the most important cytochrome P450 enzyme, namely CYP3A4, can pose practical problems for prediction of such effects. For example, while quinidine makes no distinction between two substrates for CYP3A4 (BzRes=benzoyloxyresorufin and BQ=7-benzyloxyquinoline), the drug astemizole does. Thus, the data with BQ shows astemizole to be a potent inhibitor of CYP3A4 (predicting drug–drug interactions) while the data with BzRes shows it to be relatively inactive (data from [5]).
 |
New Terminology
• Competitive inhibition: The inhibitor and substrate compete for the substrate binding site.
• Covalent bond: Chemical bond formed between the inhibitor and enzyme through alkylation.
• Irreversible inhibition: The inhibitor has a neglible rate of dissociation from the enzyme once it binds.
• Km: Michaelis–Menten constant referring to the sensitivity of an enzyme to a given substrate; it encompasses substrate binding and catalysis.
• Mechanism-based inhibition: The enzyme creates an active species through catalysis which then goes on to alkylate the enzyme and inactivate it.
• Mixed inhibition: The inhibitor has different affinities for the enzyme and enzyme–substrate complex.
• Non-competitive inhibition: The inhibitor has equal affinity for the enzyme and the enzyme–substrate complex.
• Suicide inhibitor: The inhibitor binds to the enzyme active site and irreversibly inactivates the enzyme when it does so.
• Tight-binding inhibitor: The inhibitor has a neglible rate of dissociation from the enzyme once it binds, although the bond between the inhibitor and enzyme may not be covalent.
• Uncompetitive inhibition: The inhibitor binds only to the enzyme–substrate complex.
• Vmax: The maximal rate of enzyme hydrolysis (characteristic for an enzyme–substrate pair).
Enzyme Kinetics
The model used to describe enzyme kinetics is shown in Fig. 6.1 A. Thus, a substrate binds to an enzyme (with a standard rate of association k1 and dissociation k2) and then a process of catalysis occurs (with a new rate constant kcat) which results in a product (formed from the substrate) and regeneration of the enzyme. The enzyme thus acts as a catalyst to reduce the energy barrier that separates the substrate from the product (Fig. 6.1B). Enzymes can modify a single molecule or catalyze a reaction between two molecules; this can form a single product or there can be an exchange of atoms to produce two or more different products. The formal kinetic model used to describe enzyme reactions is the Michaelis–Menten model according to the equation (see Derivations and Proofs, Appendix B10):
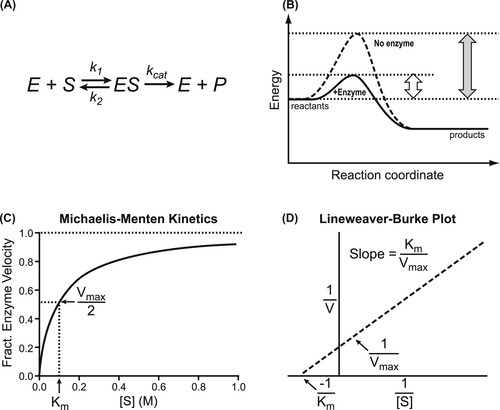 |
| Figure 6.1 Enzyme catalysis. (A) Scheme showing substrate [S] binding to enzyme [E] to form a complex [ES] which then, through kcat, converts substrate to product [P] and initiates regeneration of enzyme E. (B) This can be seen as the enzyme functioning as a catalyst to lower the energy barrier for production of the product. (C) Graphical representation of the Michaelis–Menten equation for enzyme function (equation 6.1). (D) Linear transformation of the Michaelis–Menten equation as published by Lineweaver and Burk (equation 6.3). |
(6.1)
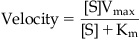
(6.2)
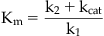
The affinity of the substrate for the enzyme is described (as for binding in the Langmuir adsorption isotherm; see equation 2.1) as Kd=k2/k1, but since this isn’t a static binding process (the reaction continues to formation of product), kcat must be included to describe the influence of catalysis on the binding process; kcat is the collective rate constant for the forward progress of the chemical steps in catalysis. Therefore, Kd does not equal Km unless kcat<<k2.
Figure 6.1C shows a graphical representation of equation 6.1; there are notable features in this relationship. For low substrate concentrations, enzyme velocity→(kcat/Km)[E][S] where [E] is the enzyme concentration. Thus the velocity of the reaction depends upon both the substrate concentration and the amount of enzyme present. Under these circumstances the reaction resembles a bi-molecular reaction with a pseudo second-order rate constant of kcat/Km. Efficient enzymes have values of kcat/Km approaching 108 to 1010M−1s−1 (this becomes diffusion-limited). With high substrate concentrations ([S]>>Km) the enzyme velocity is Vmax=kcat[E]. Under these circumstances the rate of reaction depends only on the amount of enzyme present (unimolecular reaction with pseudo first-order rate constant kcat).
The graphical relationship between substrate concentration and enzyme velocity according to the Michaelis–Menten equation (equation 6.1) is shown in Fig. 6.1C. Here it can be seen that the maximal velocity is Vmax and the half-maximal velocity is the Km (as a substrate concentration). Historically, a linear double reciprocal metameter of equation 6.1 has been used to analyze enzyme reactions according to the equation:
(6.3)
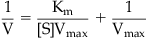
Termed the Lineweaver–Burk equation, this yields a straight line with abscissal intercept of −1/Km, an ordinate intercept of 1/Vmax and a slope of Km/Vmax (see Fig. 6.1D). Before the widespread availability of computers able to fit data directly to non-linear functions, linear transformations such as the Lineweaver–Burk plot were used to estimate parameters; these could be calculated through linear regressional analysis. However, the availability of techniques to fit data directly to the Michaelis–Menten equation has supplanted the use of linear transformations as the latter, being double reciprocal plots, can lead to seriously skewed estimates of parameters and are highly unreliable for the estimation of enzyme constants. It will be seen in future sections, however, that the Lineweaver–Burk plot can still be useful as an identifier of type of enzyme inhibition.
Enzymes as Drug Targets
Enzyme inhibitors have been used as therapeutic drugs throughout pharmacological history (see Box 6.2). There are numerous scenarios where drug intervention into an enzyme reaction can yield therapeutically favorable outcomes. These are:
Box 6.2
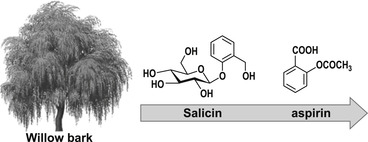
From the time of Hippocrates, (circa 460 bc to 377 bc) extracts from the bitter bark and leaves of the willow tree were known to alleviate pain and fever. In 1828, a Professor of Pharmacy at the University of Munich isolated a tiny amount of yellow needle-like crystalline bitter-tasting crystals from willow bark he called salicin. In 1897, chemists at Bayer AG led by Arthur Eichengrűn and Felix Hoffmann produced acetylsalicylic acid from salicin. Hoffmann gave the new compound to his father who was suffering from arthritis and noticed an improvement. The compound was patented in 1900, named “Aspirin” (the “A” from acetyl and spir from Spiraea ulmaria, the plant from which it was derived).
Long thought to act through the central nervous system, JohnVane and Priscilla Piper tested aspirin at the Royal College of Surgeons in London and noted that it blocked the production of what later were found to be prostaglandins. Subsequent research showed that aspirin is an irreversible inhibitor of the enzyme cyclooxygenase through acetylation of a serine residue at the active site. This gives the molecule its analgesic, anti-inflammatory and antipyretic activity.
 |
1. Enzyme inhibition to alter levels of normal physiological cellular molecules. For example, the enzyme phosphodiesterase degrades the physiologically active second messenger cyclic AMP in cardiac cells; this controls cardiac contractility and sinus rhythm. In failing hearts (congestive heart failure), a useful augmentation of contractility can be obtained by blockade of enzymatic degradation of cyclic AMP; phosphodiesterase inhibitors such as milrinone are useful in congestive heart failure. Augmentation of cardiac contractility can also be gained from blockade of ATPase enzymes in heart muscle (e.g., using digitalis) and erectile dysfunction can be treated by blockade of cyclic GMP degradation by phosphodiesterase V inhibition (sildenafil).
2. Blockade of enzyme activity that becomes pathophysiological. The renin–angiotensin system is intimately involved in blood pressure and fluid balance, and in conditions of hypertension, blockade of the angiotensin-converting enzyme (ACE) by drugs such as lisinopril lowers blood pressure. Similarly, aspirin blocks the enzyme cyclooxygenase to prevent formation of inflammatory prostaglandins and thromboxane (see Box 6.2). Inhibitors of xanthine oxidase prevent this enzyme from producing excess amounts of uric acid in gout.
3. Blockade of an enzyme that exclusively takes part in a pathophysiological process. After HIV infection and in the progression process to AIDS, HIV-1 utilizes the enzyme HIV reverse transcriptase to catalyze the production of viral DNA from the viral RNA template to facilitate further infection; drugs such as AZT (azidothymidine) effectively block this process. Penicillin is a suicide substrate that selectively blocks the enzyme that controls bacterial wall integrity to selectively destroy bacteria with no harm to the host (see Box 6.3). Similarly sulfa drugs such as sulfanilamide block dihydropteroate synthetase to prevent bacteria from synthesizing required folic acid; this is lethal to bacteria but not humans, providing a useful selective bacteriostatic action.
Box 6.3
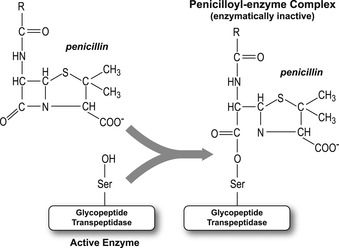
Penicillins are molecules produced by molds in the Penicillium family. Their antibiotic activity was discovered in 1928 by Alexander Fleming, but penicillins were not widely used therapeutically until the 1940s. Penicillins act as suicide substrates of glycopeptide transpeptidase in bacteria. Thus, penicillin enters the active site as a substrate, but in the normal process of catalysis forms a covalent bond to permanently inactive the enzyme. This enzyme is essential for bacterial wall cross-linking, thus inactivation by penicillin disrupts bacterial integrity and causes death. There is no corresponding process in humans, therefore the biochemical reaction is unique to bacteria; this makes penicillin a valuable antibiotic. Some bacteria have developed penicillin resistance through expression of an enzyme β-lactamase. This enzyme opens the four-membered ring of penicillins.
 |
4. Blockade of hyperactivity from enzymes. Enzyme inhibitors can be selectively lethal to cells with varying levels of metabolic activity. For example, blockade of nucleotide synthesis by drugs such as methotrexate can be selectively lethal to rapidly growing cells carrying out DNA replication in tumors. In human breast cell tumors, the over-expression of HER2 can be countered by blockers of tyrosine kinase ErbB2 such as herceptin.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


