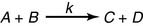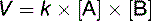Chapter 4 Enzymatic Reactions
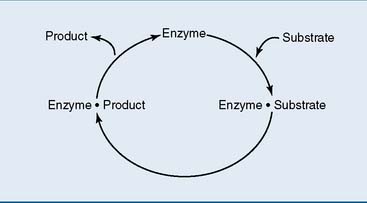
Therefore living things depend on highly selective catalysts called enzymes. By definition, a catalyst is a substance that accelerates a chemical reaction without being consumed in the process. Because it is regenerated at the end of each catalytic cycle (Fig. 4.1), a single molecule of the catalyst can convert many substrate molecules into product. Only a tiny amount of the catalyst is needed.
The equilibrium constant describes the equilibrium of the reaction
the equilibrium constant is
[B] and [A] are the molar concentrations of product B and substrate A at equilibrium.
the equilibrium constant is
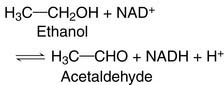
The alcohol dehydrogenase (ADH) reaction provides an example:
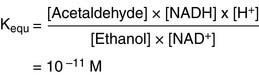
NAD+ (nicotinamide adenine dinucleotide) is a coenzyme that accepts hydrogen in this reaction (see Chapter 5). The equilibrium constant of the reaction is
From Equation (2) we can calculate the relative concentrations of acetaldehyde and ethanol at equilibrium when [NADH] = [NAD+] and pH = 7.0:
There is 10,000 times more ethanol than acetaldehyde at equilibrium!
Under aerobic conditions, however, NAD+ is far more abundant than NADH in the cell. When [NAD+] is 1000 times higher than [NADH], Equation (3) assumes the numerical values of
The pH also is important. At pH of 8.0 and [NAD+]/[NADH] ratio of 1000, for example, Equation (3) yields
The free energy change is the driving force for chemical reactions
where T = absolute temperature measured in Kelvin.
ΔG is the driving force of the reaction. Like ΔE and ΔH in Equation (4), it is measured in kilocalories per mole (kcal/mol) or kilojoules per mole (kJ/mol). A negative sign of ΔG defines an exergonic reaction. It can proceed only in the forward direction. A positive sign of ΔG signifies an endergonic reaction. It can proceed only in the backward direction. At equilibrium, ΔG equals zero.
Equation (5) shows that a reaction can be driven by either a decrease in the chemical bond energies of the reactants (negative ΔH) or an increase in their randomness (positive T × ΔS). Low energy content and high randomness are the preferred states. Like most students, Nature tends to slip from energized order into energy-depleted chaos.
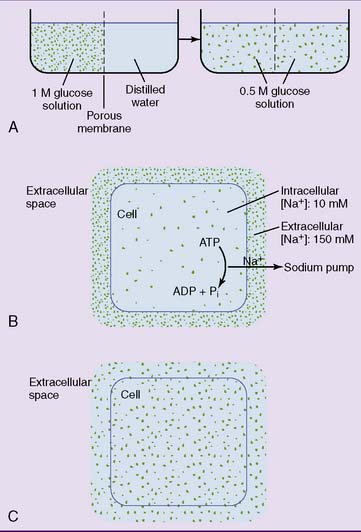
Entropy changes are small in most biochemical reactions, but diffusion is an entropy-driven process (Fig. 4.2, A). There is no making and breaking of chemical bonds during diffusion. Therefore the enthalpy change ΔH is zero. This leaves the T × ΔS part of Equation (5) as the only driving force. Thus diffusion can produce only a random distribution of the dissolved molecules.
The human body is a very orderly system. To maintain this improbable and therefore thermodynamically disfavored state of affairs, biochemical reactions must antagonize the spontaneous increase in entropy.Equation (5) shows that a reaction can reduce entropy (negative T × ΔS) only when it consumes chemical bond energy (negative ΔH). In other words, the human body must consume chemical bond energy to maintain its low-entropy state.
In the example of Figure 4.2, B and C, the cell maintains a sodium gradient across the membrane by pumping sodium out of the cell (negative T × ΔS). Sodium pumping is driven by the hydrolysis of adenosine triphosphate (ATP) to adenosine diphosphate (ADP) and inorganic phosphate (Pi) (negative ΔH). Without ATP the gradient dissipates, the entropy of the system increases, and the cell dies. That is what death and dying are all about: a sharp rise in the entropy of the body.
The standard free energy change determines the equilibrium
the standard free energy change ΔG0′ is related to the real free energy change ΔG by Equation (6):
where R = gas constant, and T = absolute temperature measured in Kelvin. The numerical value of R is 1.987 × 10−3 kcal × mol−1 × K−1. At a “standard temperature” of 25°C (298K), Equation (6) assumes the form of
At equilibrium, ΔG = 0, and Equation (7) therefore yields
Substituting Equation (9) into Equation (8) yields
There is a negative logarithmic relationship between ΔG0′ and the equilibrium constant K′equ (Table 4.1). When ΔG0′ is negative, product concentrations are higher than substrate concentrations at equilibrium; when it is positive, substrate concentrations are higher.
Table 4.1 Relationship between the Equilibrium Constant K′equ and the Standard Free Energy Change ΔG0′
| K′equ | ΔG0′ (kcal/mol) |
|---|---|
| 10−5 | 6.82 |
| 10−4 | 5.46 |
| 10−3 | 4.09 |
| 10−2 | 2.73 |
| 10−1 | 1.36 |
| 1 | 0 |
| 10 | −1.36 |
| 102 | −2.73 |
| 103 | −4.09 |
| 104 | −5.46 |
| 105 | −6.82 |
Enzymes are both powerful and selective
Enzymes can accelerate a chemical reaction enormously. Many reactions that proceed within minutes in the presence of an enzyme would require thousands of years to reach their equilibrium in the absence of a catalyst. The turnover number describes the catalytic power of the enzyme. It is defined as the maximal number of substrate molecules converted to product by one enzyme molecule per second.Table 4.2 lists the turnover numbers of some enzymes.
Table 4.2 Approximate Turnover Numbers of Some Enzymes
| Enzyme | Turnover Number (s−1)* |
|---|---|
| Carbonic anhydrase | 600,000 |
| Catalase | 80,000 |
| Acetylcholinesterase | 25,000 |
| Triose phosphate isomerase | 4,400 |
| α-Amylase | 300 |
| Lactate dehydrogenase (muscle) | 200 |
| Chymotrypsin | 100 |
| Aldolase | 11 |
| Lysozyme | 0.5 |
| Fructose 2,6-bisphosphatase | 0.1 |
* Turnover numbers are measured at saturating substrate concentrations. They depend on the assay conditions, including temperature and pH.
The substrate must bind to its enzyme before the reaction can proceed
where E = free enzyme, S = free substrate, and E·S = enzyme-substrate complex.
According to the lock-and-key model, substrate and active site bind each other because their surfaces are complementary. In many cases, however, substrate binding induces a conformational change in the active site that leads to further enzyme-substrate interactions and brings catalytically active groups to the substrate. This is called induced fit (Fig. 4.3).
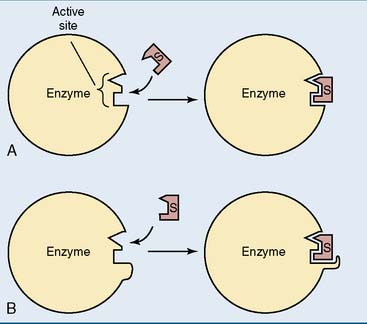
Figure 4.3 Two models of enzyme-substrate binding. A, Lock-and-key model. B, Induced-fit model. S, Substrate.
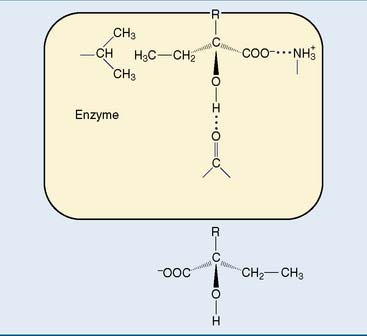
The enzyme’s substrate specificity is determined by the geometry of enzyme-substrate binding. If the substrate is optically active, generally only one of the isomers is admitted. This is to be expected because the enzyme, being formed from optically active amino acids, is optically active itself. A three-point attachment (shown schematically in Fig. 4.4) is the minimal requirement for stereoselectivity.
Rate constants are useful for describing reaction rates
The rate (velocity) of a chemical reaction can be described by a rate constant k:
In this one-substrate reaction, the reaction rate is defined by
For a reversible reaction, the forward and backward reactions must be considered separately:
At equilibrium, Vforward = Vbackward. Therefore the net reaction is zero:
Equation (15) shows that the equilibrium constant Kequ, previously defined as [B]/[A] at equilibrium, is also the ratio of the two rate constants.
The forward reaction in Equation (12) is a first-order reaction. In a first-order reaction, the reaction rate is directly proportional to the substrate concentration. When the substrate concentration [A] is doubled, the reaction rate V is doubled as well. Uncatalyzed one-substrate reactions follow first-order kinetics. A classic example is the decay of a radioactive isotope.

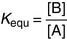

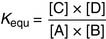
 (1)
(1) (2)
(2)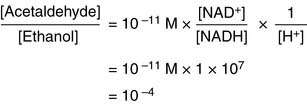 (3)
(3)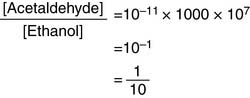
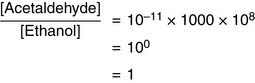
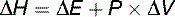
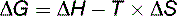
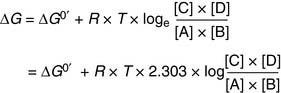 (6)
(6)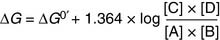 (7)
(7)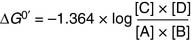 (8)
(8)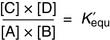 (9)
(9)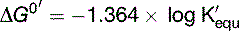

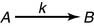
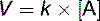
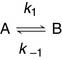 (12)
(12)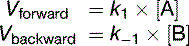
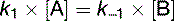
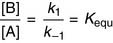 (15)
(15)