Up to this point we have mainly focussed on the issues of how we can quantify health (or ill health) and how to identify factors that might be causing ill health, with a view to preventing it in the future. In the previous chapter we alluded to what is sometimes called ‘secondary’ prevention, where instead of trying to prevent disease from occurring, we try to detect it earlier in the hope that this will allow more effective treatment and thus improved health outcomes. This is an aspect of public health that has great intuitive appeal, especially for serious conditions such as cancer where the options for primary prevention can be very limited. However, screening programmes are usually very costly exercises and they do not always deliver the expected benefits in terms of improved health outcomes (see Box 15.1). In this chapter we will introduce you to the requirements for implementing a successful screening programme and to some of the problems that we encounter when trying to determine whether such a programme is actually beneficial in practice. Box 15.2 summarises the various stages in this process and the central role of epidemiology in all of these.
In the 1960s, public health practitioners were seduced by the concept of early diagnosis – give people regular health checks to identify and treat disease early. It seemed so obvious it would work that initiatives of this type started springing up in the USA and the UK. The UK Ministry of Health realised that the cost implications were enormous, so between 1967 and 1976 a trial was conducted in London to evaluate the benefits of multiphasic screening of middle-aged adults in general practice. Approximately 7000 participants were randomly allocated to receive either two screening checks two years apart or no screening and all participants then underwent a health survey. The investigators did not find any significant differences between the two groups in terms of their morbidity, hospital admissions, absence from work for sickness, or mortality. The only outcome appeared to be the increased costs of healthcare – approximately £142 million to screen the entire middle-aged UK population (and that was at 1976 prices). (The South-East London Screening Study Group, 1977; reprinted in 2001 with a series of commentaries, Various, 2001.)
Epidemiology has multiple roles to play in screening, from the initial decision-making on whether or not to use screening to help control a disease through to assessment of whether the screening works in practice. Elements of this (and the relevant study designs) include:
identifying whether a disease has an appropriate ‘natural history’ to make screening an option (descriptive case series);
considering if it conveys a significant burden (estimates of incidence, prevalence, mortality and overall burden e.g. in the form of DALYs);
measuring test quality and estimating how it might perform in the population (cross-sectional studies);
assessing the potential of a screening programme to improve outcomes while dealing with special forms of selection bias (RCTs); and finally
evaluating the performance of the programme in practice (long-term descriptive and ecological coverage of regions and nations).
This dependence on the sound design and interpretation of a broad mix of epidemiological studies to determine the quality and practical utility of a screening programme emphasises the central role of epidemiology in health services assessment and policy evaluation.
Why screen?
It has been known for some time that infection with human papillomavirus (HPV) is a major and probably necessary cause of cervical cancer (see Chapter 10), but until the development of HPV vaccines in recent years we could not prevent people from becoming infected, other than through encouraging condom use. As uptake of these vaccines becomes widespread, they may eventually replace the current screening programmes as the preferred method for control of this disease. However, the screening programmes have shown that in the absence of primary preventives like vaccines, detecting disease before the usual time of diagnosis can provide an effective ‘second level’ of public health intervention.
When used as a public health measure for disease control, screening implies the widespread use of a simple test for disease in an apparently healthy (asymptomatic) population. A screening test will often not diagnose the presence of disease directly, but will instead separate people who are more likely to have the disease from those who are less likely to have it. Those who may have the disease (i.e. those who screen positive) can then undergo further diagnostic tests and treatment if necessary. The improved public health outcomes we seek through screening are reduced morbidity, mortality and/or disability. The benefits of public health screening are primarily for those people who are actually screened, and generally even among this group only very few will benefit directly, but there may also be wider social benefits if overall health costs are reduced.
Screening is also used, in a slightly different fashion, to protect the general population from exposure to disease. As an example, immigrants to a number of countries are screened for HIV and hepatitis B infection; and travellers from regions with epidemic acute infectious diseases, such as Ebola, SARS (severe acute respiratory syndrome) or H1N1 influenza, have been subjected to screening using health declaration cards to identify symptoms and sometimes thermal scanning to detect signs of infection at airports. The primary aim of this type of screening is not to benefit the individual who is screened, but to protect the local population from these viruses. Similarly, some occupations require regular screening; for example, airline pilots have regular medical checks in an attempt to ensure that they will not have a heart attack while flying. Insurance companies often require people to undergo health checks and screening before they offer them a life insurance policy. Here the ‘screening’ is done for purely financial reasons, because insurance companies charge higher premiums for people at higher risk.
The disease process
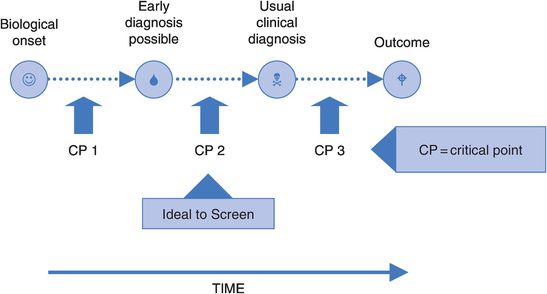
The first we know of the existence of a disease in a person is when it is diagnosed. This is usually some time after it first produces the symptoms which cause the person to seek medical care. The actual onset of disease will of course be earlier than this – how much earlier depends on the disease concerned. Figure 15.1 illustrates this point.
At some stage between the biological onset of disease and the time of usual clinical diagnosis there may come a time when early signs of disease are there, if only we could detect them. The position of this point will vary depending on the disease, perhaps occurring many years before the appearance of clinical disease (e.g. high blood pressure, some cancers), or only shortly before symptoms appear (e.g. acute infectious diseases).
At some stage during the disease process there is also likely to be a critical point, after which the disease process is irreversible and treatment will confer little or no benefit. An example is the point at which a cancer starts spreading to other tissues (known as metastasis). If this ‘point of no return’ occurs before it is possible to detect the disease (CP 1 in Figure 15.1), then advancing the time of detection will simply mean that the person knows about their disease for longer but their outcome will not be improved. Similarly, if this point occurs after the time of usual clinical diagnosis (CP 3) there is no need to detect the disease any earlier, given that treatment following usual diagnosis will be effective.
Screening, then, is of greatest potential benefit when the critical point occurs between the time of first possible detection and the usual time of diagnosis (CP2). In this situation it may be that picking up the disease early would improve outcomes, and this is the aim of a screening programme. Unfortunately, we currently have too little knowledge of the progress of most diseases for this to have much practical value in planning screening programmes.
Screening versus case-finding
There is considerable debate about the best way to implement early detection of disease. Should the focus be on large-scale mass population screening, or are we better off pursuing opportunistic early detection or ‘case-finding’ when someone comes into contact with the health system for another reason? There are some parallels here with the mass versus high-risk approach to primary prevention that we discussed in the previous chapter. The terms ‘screening’ and ‘case-finding’ can also have quite different meanings to different practitioners. We think it is most useful, and best accepted, to use the term ‘screening’ for organised population-wide approaches and ‘case-finding’ for more opportunistic attempts at early detection. If systematically applied, case-finding can nonetheless form the basis for quite good population coverage. For example, if a large proportion of the people visit a primary care physician every year or two, this contact could permit early detection of risks (e.g. from cigarette smoking, high blood pressure) in a setting that allows good follow-up.
The requirements of a screening programme
Screening differs from diagnostic testing in that it is performed before the development of clinical disease. Thus, those who undergo screening are free, or appear to be free, of the disease of interest. They are not seeking care because they are sick, but are instead persuaded to be screened by the health service. The requirements of a screening test are therefore somewhat different from those of a diagnostic test, which is performed only when someone is suspected to have a disease. While both should be as accurate as possible (see below), the screening test will often sacrifice some accuracy as it also has to be relatively cheap, very safe, and acceptable to someone who has no symptoms. Critically, though, an accurate test for a disease is not sufficient to justify a community screening programme. The suitability of a disease for screening has to be considered explicitly before all else and, finally, the whole programme must be shown to confer a net benefit to the community.
The disease
We need to consider the following characteristics of a disease before deciding whether screening for it may be desirable.
Prostate cancer shows us the importance of this. It appears to occur in a number of biological forms that we cannot tell apart, and it is probable that many men in whom a cancer could be detected by screening (e.g. with a prostate-specific antigen (PSA) test) would never develop symptoms or suffer from the disease (and therefore would not otherwise be diagnosed). This has been clearly seen in a number of studies of autopsies showing that many men who died of other diseases had microscopic cancers present in their prostate glands (Martin, 2007). To detect and treat these men would be wholly harmful and, largely for this reason, screening for prostate cancer is generally not recommended, even though there are tests that could be used (and which are used quite widely in some countries, e.g. the USA, on an ad-hoc case-finding basis). Research is under way in a number of countries in an attempt to shed light on this dilemma to allow a more informed judgement to be made.
In general, there should be a high prevalence of pre-clinical (early-stage) disease.
This criterion becomes less important as the severity of the disease increases. For example, it may be of benefit to screen for a fairly uncommon disease if not treating it has severe consequences – an example is the use of screening for phenylketonuria (PKU) in newborns. Babies born with this condition lack an enzyme that metabolises the amino acid phenylalanine. When they eat proteins containing this amino acid, the end-products accumulate in the brain, leading to severe mental retardation. By simply restricting the phenylalanine in their diet this can be prevented. Although only about one in 15,000 babies is born with this condition, the availability of a simple, accurate and inexpensive test makes it worthwhile to screen all newborn babies (Wilcken et al., 2003).
Screening is likely to be more effective if there is a long period between the first detectable signs of disease and the overt symptoms that normally lead to diagnosis (the lead time).
If a disease progresses rapidly from the pre-clinical to clinical stages, i.e. the interval between the point when early diagnosis is theoretically possible and when clinical diagnosis would usually occur (see Figure 15.1) is short, then it is much harder to detect the disease by screening because this would have to occur within this narrow time window to have any benefit. (Clearly, metabolic conditions of early life, such as PKU, are exceptions to this because screening can be done at birth.)
The screening test
The next requirement for a worthwhile screening programme is that we have a test that will enable us to detect the disease before the usual time of diagnosis. Any such test must meet the following criteria.
Firstly it should be accurate.
As discussed in Chapter 7, accuracy reflects the degree to which the results of the test correspond to the true state of the phenomenon being measured. In practice, accuracy can be influenced by the standardisation or calibration of the testing apparatus and by the skill of the person conducting or interpreting the test. Maintaining high standards of testing in a service setting is thus crucial for a screening programme to reach its full potential.
So what should we expect of a screening test in relation to its accuracy? We would expect it to be:
sensitive – ideally it would identify all people with the disease; in practice, itshould identify most of these people;
specific – ideally it would identify only those with that particular disease andthose without the disease should test negative; in practice, most of those without the disease should test negative.
The measures of sensitivity and specificity are also used to determine the accuracy of a diagnostic test (see Box 15.3).
Because we are advising apparently well people to undergo screening, we should not offer them a test that might adversely affect their health. The only exception might be for those at very high risk of developing a serious disease, when a slight risk from screening might be outweighed by a large benefit of early diagnosis (e.g. regular colonoscopy for people with ulcerative colitis, who develop large bowel cancer at a high rate). Social and cultural acceptability are separate issues and are seldom related to the safety of the screening test. For example, the requirement to take a sample of their faeces to test for blood as an early indicator of colon cancer is unpalatable to many. Likewise, cervical cancer screening is not immediately appealing in many societies and in some it may be prohibited, particularly if the health professional is male.
It should be simple and cheap.
If we wish to screen a large proportion of the population any test used should be relatively cheap to administer and simple to perform or it would be too costly to perform large-scale screening.
Although mammography is neither simple nor cheap, breast cancer is a severe disease of substantial concern to many communities. It occurs relatively commonly and, if detected early, is usually highly treatable, with better outcomes than when treated later.
Test quality: sensitivity and specificity
We can evaluate the performance of a test by comparing the results with a ‘gold standard’ method that ideally would give 100% correct results (but more commonly is just the best test available). This standard might be a more costly or time-consuming test, or perhaps a combination of investigations performed in hospital that is reliable for diagnosis but unsuitable for routine use in screening.
For example, children in many countries undergo a simple hearing test in their first year at school. Any who fail this screening test are retested at a later date and/or referred to a hearing clinic for further, more extensive tests to identify whether they have a real hearing problem. Imagine that in a group of 500 children, 50 have a genuine hearing problem. Of these, 45 fail the school hearing test, as do 30 of the children with normal hearing (perhaps they had a cold on the day of the test).
Summarise the results of the test in a table, including labels for the rows and columns.
Your table should look something like Table 15.1.
| School hearing test | True hearing status | ||
|---|---|---|---|
| Hearing problem | Normal | Total | |
| Fail (positive test result) | 45 | 30 | 75 |
| Pass (negative test result) | 5 | 420 | 425 |
| Total | 50 | 450 | 500 |
There are four possible outcomes for a child, as shown in Figure 15.2. A child with a real hearing problem may either fail the screening test (true positive; group ‘a’ in Figure 15.2) or pass the test, suggesting falsely that they do not have a problem (false negative; group ‘c’). Similarly, a child without a problem may pass the test (true negative; group ‘d’) or fail, falsely implying that they do have a problem (false positive; group ‘b’).
Possible outcomes from a screening test.
For a test to be accurate it should produce few false positive and false negative results. So how good is the school hearing test? There are two issues to consider: how well has the test identified the children who do have a problem; and how well has it classified the normal children as normal?
What percentage of children with a real hearing problem failed the school test?
What percentage of children with normal hearing passed the school test?
Looking at Table 15.1, we see that 90% (45 ÷ 50) of children with a hearing problem failed the school test and 93% (420 ÷ 450) of children with normal hearing passed the test. These measures of a test are known, respectively, as its sensitivity and specificity.
The sensitivity of a test measures how well it classifies people with the condition as ‘sick’. It is the percentage of people with the condition who test positive (90% in the example above). It is calculated by dividing the number of true positive results (a) by the total number of people with the condition (a + c) from Figure 15.2:
(15.1)The specificity of a test measures how well it classifies people without the condition as ‘healthy’. It is the percentage of people without the condition who test negative (93% in the above example). To calculate it, we divide the number of true negative results (d) by the total number of people without disease (b + d):
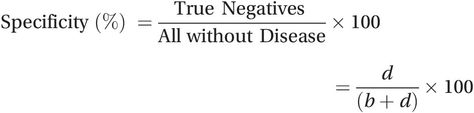(15.2)A combination of high sensitivity and high specificity is essential for a good screening test – in this regard, the school hearing test works quite well.
Note that it is necessary to do a special (cross-sectional) study, as discussed in ‘Diagnostic studies’ in Chapter 4 (Box 4.7), to assess the sensitivity and specificity of a test. In the service setting, usually only those who test positive (groups ‘a’ and ‘b’ from Figure 15.2) will be followed up with formal diagnostic testing to determine the true positives. Those who test negative are not normally followed up, so the proportion of false negatives is not known and we cannot measure either the sensitivity or the specificity of the test.
Test performance in practice: positive and negative predictive values
Two other measures tell us how well a test performs in a given population. In practice we do not know at the point of testing whether a child does have a real hearing problem – we have to predict this from the screening test result. We therefore need to know how well a positive test result (i.e. failing the hearing test) predicts that a child really does have a hearing problem and, conversely, how well a negative test result (i.e. passing the hearing test) predicts that their hearing is normal.
What percentage of children who failed the school hearing test had a real hearing problem?
What percentage of children who passed the school hearing test really did have normal hearing?
Out of 75 children who failed the school hearing test, 45 (60%) had a real hearing problem. Out of 425 children who passed the school test, 420 (99%) really did have normal hearing.
These measures are known respectively as the positive and negative predictive values (PPV and NPV) of the test in that situation. Unlike the sensitivity and specificity, they are not fixed properties of the test because, as you will see below, they also depend on the prevalence of the condition in the population being tested.
The positive predictive value (PPV) tells us how likely it is that a positive test result indicates the presence of the condition. It is the percentage of all people who test positive who really have the condition (60% in the example). It is calculated by dividing the number of true positive results (a) by the total number of positive results (a + b):
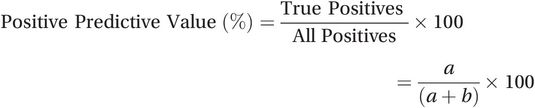(15.3)The negative predictive value (NPV) is the percentage of all people who test negative who really do not have the condition (99% in the example). To calculate it, simply divide the number of true negative results (d) by the total number of negative results (c + d):
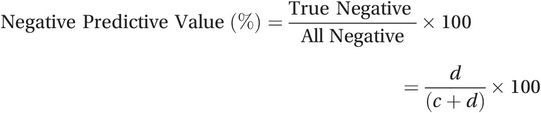(15.4)These measures of test performance are best thought of as operational measures of the overall programme. They reflect both the accuracy of the test (sensitivity and specificity) and the prevalence of the condition in the population tested. Even a superb test (very high sensitivity and specificity) will yield a low PPV if the condition is rare.
An example – testing blood donors for HIV infection
It is routine practice in most countries to screen all blood donors for HIV, but what is the probability that someone who tests positive really is infected with HIV?
What measure do we need to calculate to answer this question?
To answer this, we must calculate the positive predictive value of the test. Assume that we are using the test to screen a high-risk population of intravenous drug users in New York City who have an HIV prevalence of 5500 per 10,000. Using this information and your answers to the following questions, construct a table similar to Table 15.1 to show these data.1
How many in a group of 10,000 intravenous drug users would you expect to have HIV infection?
Of these, how many would test positive if the test had a sensitivity of 99.5%, and how many would falsely test negative?
How many of the drug users will not be HIV-positive and, of them, how many would test negative if the test had a specificity of 99.5%? How many would falsely test positive?
What proportion of the people who test HIV-positive would truly have HIV infection?
Given the known prevalence of HIV infection in this group, we would expect 5500 of the 10,000 intravenous drug users to be HIV-positive and the remaining 4500 would be HIV-negative, giving the ‘total’ row at the bottom of the table. Of the HIV-positive group, 99.5% or 5473 would correctly test positive and the remaining 27 would falsely test negative (giving the numbers for cells a and c in the table) and among the HIV-negative group 99.5% or 4478 would correctly test negative (d) and the remaining 22 would falsely test positive (b). Your table should then show a total of 5495 positive test results, of which 5473 or 99.6% are true positives (the PPV). Similarly, of the 4505 negative test results, 4478 or 99.4% are true negatives (the NPV). The test therefore performs very well in this high-risk population.
Now repeat the calculations for a low-risk population of new blood donors where the prevalence of HIV is only 4 per 10,000.
Among the blood donors we would expect only about 4 out of 10,000 people to be truly HIV-positive and the remaining 9996 would be HIV-negative. All four of the HIV-positive people should correctly test positive (Table 15.2). Among the HIV-negative group 99.5% or 9946 would correctly test negative and the remaining 50 would falsely test positive. This means that we now have a total of 54 positive test results but, of these, only 4 or 7.4% are true positives (PPV). This means that 93% or more than 9 of every 10 positive test results would be false positives.
| Test | True HIV status | |||
|---|---|---|---|---|
| Positive | Negative | Total | ||
| Intravenous drug users | ||||
| Positive | 5,473 | 22 | 5,495 | PPV = 5,473 ÷ 5,495 = 99.6% |
| Negative | 27 | 4,478 | 4,505 | NPV = 4,478 ÷ 4,505 = 99.4% |
| Total | 5,500 | 4,500 | 10,000 | |
| New blood donors | ||||
| Positive | 4 | 50 | 54 | PPV = 4 ÷ 54 = 7.4% |
| Negative | 0 | 9,946 | 9,946 | NPV = 9,946 ÷ 9,946 = 100% |
| Total | 4 | 9,996 | 10,000 | |
Thus, even with a very high sensitivity and specificity, the same test performs badly in this low-risk population. The profound influence of changes in disease prevalence and test accuracy on the positive predictive value of a test is shown in Table 15.3. In practice, the lower values for sensitivity and specificity included in the table are often encountered, and for most diseases of consequence the prevalence in the general population is also quite low; for example, recent Australian data suggest the prevalence of breast cancer among women aged 50–69 who attend for mammographic screening (the target age group) is around 0.3% (AIHW and NBOCC, 2009).
The prevalence of prostate cancer in 60-year-old men is approximately 1%. Using Table 15.3, how accurate would you want an ultrasound screening test to be before you would consider starting a screening programme to detect early prostate cancer?
| Prevalence (%) | Sensitivity and specificitya | |||
|---|---|---|---|---|
| 99% | 95% | 90% | 80% | |
| 20 | 96.1% | 82.1% | 69.2% | 50.0% |
| 10 | 91.7% | 67.9% | 50.0% | 30.8% |
| 5 | 83.9% | 50.0% | 32.1% | 17.4% |
| 1 | 50.0% | 16.1% | 8.3% | 3.9% |
| 0.1 | 9.0% | 1.9% | 0.9% | 0.4% |
a Assuming, for convenience, that sensitivity and specificity have the same value.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
