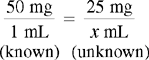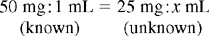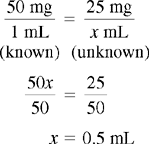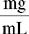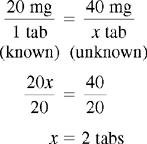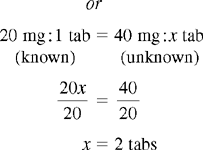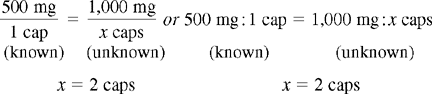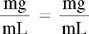Dosage Calculation Using the Ratio and Proportion Method

CHAPTER 14


Dosage Calculation Using the Ratio and Proportion Method



Objectives


After reviewing this chapter, you should be able to:


1. State a ratio and proportion to solve a given dosage calculation problem


2. Solve simple calculation problems using the ratio and proportion method


Several methods are used for calculating dosages. The most common methods are ratio and proportion and use of a formula. After presentation of the various methods, students can choose the method they find easiest and most logical to use. First, let’s discuss calculating by using ratio and proportion. If necessary, review Chapter 4 on ratio and proportion.



USE OF RATIO AND PROPORTION IN DOSAGE CALCULATION


Ratio and proportion is useful and easy to use in dosage calculation, because it is often necessary to find only one unknown quantity. Recall that a proportion is a relationship comparing two ratios.


For example, suppose you had a medication with a dosage strength of 50 mg per 1 mL, and the prescriber orders a dosage of 25 mg. A ratio and proportion may be used to determine how many milliliters to administer.


When setting up the ratio and proportion using the fraction format to calculate dosages, the known ratio is what you have available, or the information on the medication label, and is stated first (placed on the left side of the proportion). The desired, or what is ordered to be administered, is the unknown (placed on the right side). Therefore using the example the ratio and proportion would be stated as follows:






Example 1:

50 mg:1 mL=25 mg:x mL(known)(unknown)


image



Solution:

To solve for x, use the principles presented in Chapter 4 on ratio and proportion.


50 mg1 mL=25 mgx mL(known)(unknown)50x50=2550x=0.5 mL


image

Remember that, as shown, the known is stated as the first fraction, and the unknown as the second. When stated in fraction format, solve by cross multiplication.


or50 mg:1 mL=25 mg:x mL(known)(unknown)50x=product of extremes25=product of means50x=25 is the equation50x50=2550(Divide both sides by 50, the number in front of x.)x=0.5mL


image



NOTE


As shown in Chapter 4 on ratio and proportion, a proportion could be stated in fraction format or using colons.




CAUTION


It is important to remember when stating ratios that the units of measure should be stated in the same sequence (in the examples, mgmLimage = mgmLimage or mg:mL = mg : mL). Labeling the terms in the ratios, including x, is also essential. These pointers are crucial to preventing calculation errors.





Example 3:

Order: 1 g p.o. of an antibiotic


Available: 500 mg capsules. How many capsules will you administer?



Solution:

Notice that the dosage ordered is in a different unit from what is available. Proceed first by changing the units of measure so they are the same. As shown in Chapter 8, ratio and proportion can be used for conversion.


After making the conversion, set up the problem and calculate the dosage to be given. In this example the conversion required is within the same system (metric).


In this example grams are converted to milligrams by using the equivalent 1,000 mg = 1 g. After making the conversion of 1 g to 1,000 mg, the ratio is stated as follows:


500 mg1 cap=1,000 mgx capsor500 mg:1 cap=1,000 mg:x caps(known)(unknown)(known)(unknown)x=2 capsx=2 caps


image

An alternate method of solving might be to convert milligrams to grams. In doing this, 500 mg would be converted to grams by using the same equivalent: 1,000 mg = 1 g. However, decimals are common when measures are changed from smaller to larger in the metric system: 500 mg = 0.5 g. Even though converting the milligrams to grams would net the same final answer, conversions that net decimals are often the source of calculation errors. Therefore if possible, avoid conversions that require their use. As a rule, it is best to convert to the measure stated on the medication label. Doing this consistently can prevent confusion. As with the other examples, this proportion could be stated as a fraction as well.


For the purpose of learning to calculate dosages by using ratio and proportion, this chapter emphasizes the mathematics used to calculate the answer. Determining whether an answer is logical is essential and necessary in the calculation of medication. An answer must make sense. Determining whether an answer is logical will be discussed further in later chapters covering the calculation of dosages by various routes.



Points to Remember


Important Points When Calculating Dosages Using Ratio and Proportion




• Make sure all terms are in the same unit and system of measure before calculating. If they are not, a conversion will be necessary before calculating the dosage.


• When conversion of units is required, conversions can be made by converting what is ordered to the units in which the medication is available or by changing what is available to the units in which the medication is ordered. Be consistent as to how you make conversions. It is usual to convert what is ordered to the same unit and system of measure you have the medication available in.


• When stating ratios, the known is stated first. The known ratio is what is available or on hand or the information obtained from the medication label.


• The unknown ratio is stated second. The unknown ratio is the dosage desired, or what the prescriber has ordered.


• The terms of the ratios in a proportion must be written in the same sequence.


    Example: mg : mL = mg : mL or mgmL=mgmLimage.


• Label all terms of the ratios in the proportion, including x.


• Before calculating the dosage, make a mental estimate of the approximate and reasonable answer.


• Label the value you obtain for x (e.g., mL, tabs). Double-check the label for x by referring back to the label of x in the original ratio and proportion; it should be the same.


• A proportion can be stated in a horizontal fashion using colons or as a fraction.


• Double-check all work.


• Be consistent in how ratios are stated and conversions are done.


• An error in the setup of the ratio and proportion can cause an error in calculation.

Related posts:

  1. Apothecary and Household Systems
  2. Heparin Calculations
  3. Reading Medication Labels
  4. Calculation of Oral Medications

Stay updated, free articles. Join our Telegram channel
Tags:
Feb 11, 2017 | Posted by in PHARMACY | Comments Off on Dosage Calculation Using the Ratio and Proportion Method

Full access? Get Clinical Tree
Get Clinical Tree app for offline access