CHAPTER 16 After reviewing this chapter, you should be able to: 1. Define dimensional analysis 2. Implement unit cancellation in dimensional analysis 3. Perform conversions using dimensional analysis Now let’s look at the basics in using dimensional analysis for converting units of measure. It is necessary to state the equivalent (conversion factor) in fraction format, maintaining the desired unit in the numerator. An equivalent (conversion factor) will give you two fractions: Let’s look at examples to demonstrate the dimensional analysis process.
Dosage Calculation Using the Dimensional Analysis Method
UNDERSTANDING THE BASICS OF DIMENSIONAL ANALYSIS
Performing Conversions Using Dimensional Analysis
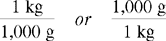
To Make Conversions Using Dimensional Analysis
Dosage Calculation Using the Dimensional Analysis Method

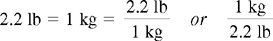
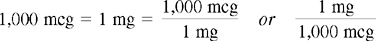
 Critical Thinking
Critical Thinking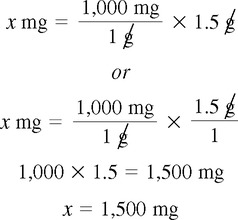
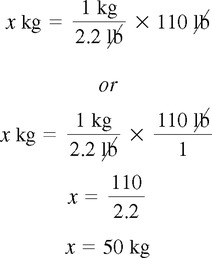
 Practice Problems
Practice Problems

