Chapter 7
Cross-over trials
7.1 Introduction
In earlier chapters, we have considered parallel group designs, where each subject is randomised to receive one of a number of alternative treatments. In contrast, in cross-over trials, subjects are randomised to receive different sequences of treatments, with the outcome being assessed for each treatment period. As before, we have a choice in analysis between fixed effects models and random effects models. In this context, we describe the treatment effect as being crossed with a random effect (subjects).
The vast majority of cross-over trials that are carried out in practice have the same basic design. Every subject receives each of the treatments being evaluated, for a standard period of time, with the outcome variables being assessed in the same way in each period of treatment. The simplest and most commonly encountered such design employs just two treatments and is often referred to as a 2 × 2 cross-over trial or as an AB/BA design. The use of this design with normally distributed data will be covered in some depth in Section 7.3. The use of more than two treatments with patients receiving every treatment is known as a higher order complete block design and is covered in Section 7.4. More complicated designs are considered in Sections 7.5 and 7.6. In Section 7.7, we will show how covariance pattern models can be employed in the analysis of cross-over trials. The following two sections (7.8 and 7.9) will give examples of the analysis of binary data and categorical data in the setting of cross-over trials. Data following Poisson distributions are not directly covered but follow the same generalised linear mixed model approach used for binary data. Section 7.10 will consider the use of information from random effects models in the planning of future studies. The chapter finishes with a discussion of some general points in relation to the analysis of cross-over trials (Section 7.11).
7.2 Advantages of mixed models in cross-over trials
Random effects models can be expected to give more precise estimates of treatment effects in situations where it is possible to recover extra information on treatments from the between-patient error stratum. The most common situation in which this occurs is where there are missing data, irrespective of the particular cross-over design used. It also occurs for the unbalanced designs considered in Sections 7.5 and 7.6. In the balanced situations, which we meet with complete block designs, the results of a fixed effects analysis and a random effects analysis will generally be identical in the absence of missing data.
A very different application of mixed models to cross-over trials arises from the covariance pattern approach. By regarding the results in successive treatment periods as a form of repeated measures data, we can examine various ways to model the covariance between repeated observations on the same patients. This can lead to greater flexibility in the interpretation of the data than with conventional analyses, and we examine examples using this approach in Section 7.7.
7.3 The AB/BA cross-over trial
This design employs two treatments (A and B) and two treatment periods. Patients are randomised to receive either the AB sequence of treatments or the BA sequence. We met a simplified hypothetical example of such a trial in Section 1.2. At that time, for simplicity of presentation, we assumed that there was no effect of the period in which treatments were received. However, such an effect is always possible, and we recommend that such an ‘order’ effect should be included in the analysis. Our initial example was also restricted to single observations in each treatment period. In practice, the randomisation to the AB or BA sequence is often preceded by a run-in period. This approach has the advantage that patients showing poor compliance can be removed prior to randomisation, and the stability of the patient’s condition can be assessed. With or without this run-in period, baseline levels for the outcome variables are usually recorded prior to randomisation. Following the first treatment period, there is often a ‘washout’ period prior to the commencement of the second treatment, and a second ‘baseline’ observation may be made. Details of design considerations, and analytical methods for a fixed effects analysis, are given in Senn (2002).
If all patients complete the trial without any missing values being generated for the outcome variables, the results of the fixed effects analysis and an analysis in which patient effects are regarded as random will usually be identical. This arises because of balance over random effects in the design, as discussed in Section 1.6. However, note that an exception occurs when the estimate of the patient variance component is negative and is set to zero. The standard errors of the treatment differences will then be lower with the random effects model. It is common for missing values to occur, usually because of premature patient withdrawal from the trial. In the fixed effects analysis of such a trial, observations from subjects with a missing value are not used because all of the information in the single remaining observation would be needed to estimate the patient effect. When missing values do occur, and a random effects analysis is performed, the data from subjects with a single period of observation are utilised in the analysis in conjunction with the complete observations to improve the efficiency of treatment comparisons relative to the fixed effects analysis. This benefit was illustrated in Section 1.2 using the earlier example but with two observations deleted.
More generally, we will now consider a cross-over trial to compare treatments A and B, with N patients divided equally between the AB and the BA sequence, following Brown and Kempton (1994). We will also assume that a proportion, p, of patients only provide data for the first treatment period. On the assumption that these dropouts are also equally divided between the two treatment sequences, we will investigate the effect of p and the variance components on the relative efficiency of the random effects and fixed effects models in estimating treatment differences. To do this, we will look first at the variance of the estimate of treatment differences, varW(A − B), obtained from within-patient comparisons. This will give the variance appropriate to the fixed effects analysis. We will then look at the corresponding term from the between-patient comparison, using those patients who only have an observation in the first treatment period. We will then pool these two estimates and obtain the variance of the pooled estimate. In this situation, this will correspond to the results of fitting a random effects model, and we will compare the variances of the fixed effects and random effects model treatment estimates.
Within-patient comparisons From our definitions, there will be N(1 − p) patients with complete data. If the residual variance is 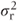 , then
, then
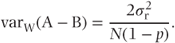
Between-patient comparisons Each treatment sequence will yield Np/2 patients with observations in the first period only. The variance of individual observations will be the sum of the residual variance 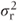 and the between-patient component
and the between-patient component 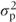 . Hence
. Hence
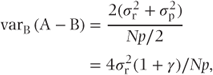
where
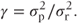
Pooled comparisons If we obtain a weighted average of the treatment effect from the within-patient and between-patient estimates, using weights inversely proportional to the variances, then we have the standard result that
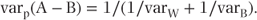
Thus,
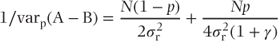
and
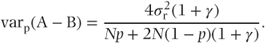
Relative efficiency The ratio of the variance of the treatment estimate using a fixed effects (within-patient) approach, to that using a random effects model (pooled), is plotted against p, the proportion of missing observations in the second period, for a range of values of γ, in Figure 7.1. From this figure, we can see that the recovery of between-patient information is most beneficial when γ is small, that is when the between-patient variance component is small. If the proportion of missing values is small, the benefit from analysis with a mixed model will be correspondingly small, although we can expect some reduction in the variance of the treatment estimate.
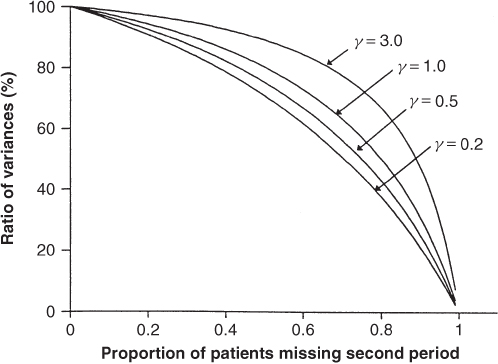
Figure 7.1 Ratio of variances of treatment differences, with and without recovery of between-patient information.
7.3.1 Example: AB/BA cross-over design
We illustrate the AB/BA cross-over design with results from an unpublished study comparing two diuretics in the treatment of mild to moderate heart failure. After initial screening for suitability, there was a period of not less than 1 day and not more than 7 days, where diuretic treatment was withheld. Immediately prior to randomisation to either the AB sequence of treatment or the BA sequence, baseline observations were taken. Each treatment period lasted for 5 days, with an immediate transfer to the second treatment after the first treatment period was completed. As a washout was not employed between treatments, observations made in the first 2 days of each treatment period were not utilised in the analysis of the trial. The primary outcome measures were the frequency of micturition and the subjective assessment of urgency. As neither of these is suitable for illustrating the analysis of normally distributed data, we will instead use a secondary effectiveness variable, namely oedema status, together with diastolic blood pressure (DBP). Oedema status is formed by the sum of the left and right ankle diameters. The DBP was calculated from the mean of three readings. Both of these variables are measured prior to randomisation and at the end of each treatment period.
In total, 101 patients were recruited for the study, but seven withdrew prior to randomisation. Of the remaining 94 patients, only two failed to complete both treatment periods. Therefore, in order to illustrate the alternative methods of analysis, we have systematically removed approximately one in five of the observations from the second period. The structure of the data as analysed is shown in Table 7.1.
Table 7.1 Data structure for a cross-over trial comparing two diuretics in patients with heart failure.
| Baseline values | Post-treatment values | |||||
| Patient | Treatment | Period | Oedema | DBP | Oedema | DBP |
| 1 | B | 1 | 45 | 60 | 45 | 55 |
| 1 | A | 2 | 45 | 60 | 45 | 60 |
| 2 | A | 1 | 51 | 50 | 48 | 60 |
| 2 | B | 2 | 51 | 50 | 48 | 65 |
| 3 | A | 1 | 53 | 70 | 50 | 70 |
| 3 | B | 2 | 53 | 70 | 52 | 80 |
| 4 | B | 1 | 49 | 68 | 47 | 60 |
| 4 | A | 2 | 49 | 68 | 47 | 60 |
| 5 | A | 1 | 46 | 65 | 45 | 60 |
| 6 | A | 1 | 61 | 95 | 60 | 95 |
| 6 | B | 2 | 61 | 95 | 59 | 97 |
For each of our outcome variables, four analyses have been performed. In all of them, a treatment effect and a period effect were included as fixed. In two of the models, the baseline level was also included in the model as a covariate. Whether or not the baseline is included in the model, separate models are considered with the patient effect being fitted either as random or as fixed. The results of the models are summarised in Table 7.2.
Table 7.2 Analysis of cross-over trial of diuretics in heart failure.
| Model | Fixed effects | Random effects | ||
| 1 | Treatment, period, patient | – | ||
| 2 | Treatment, period | Patient | ||
| 3 | Treatment, period, patient, baseline | – | ||
| 4 | Treatment, period, baseline | Patient | ||
| Treatment effect: A–B (SE) | ||||
| Model | Oedema | DBP | ||
| 1 | 0.304 (0.120) | 0.812 (0.775) | ||
| 2 | 0.301 (0.120) | 0.926 (0.765) | ||
| 3 | 0.304 (0.120) | 0.812 (0.775) | ||
| 4 | 0.309 (0.118) | 1.013 (0.748) | ||
| Variance components (SE) | ||||
| Model | Patient | Residual | Patient | Residual |
| 1 | – | 0.530 | – | 22.19 |
| 2 | 66.825 | 0.530 | 76.77 | 22.25 |
| 3 | – | 0.530 | – | 22.19 |
| 4 | 3.763 | 0.526 | 25.60 | 21.91 |
Examination of the variance component terms shows that for all models the patient term is larger than the residual term. This indicates that there may have been substantial benefits from employing a cross-over design rather than a parallel group design. We note that this is particularly striking for oedema status. Note also the effect of including the baseline as a covariate in the analysis. This has the effect of reducing the size of the patient variance component term in Model 4. The implications of this are that the benefits of the cross-over are somewhat reduced when a (highly correlated) baseline covariate is available and, conversely, that the use of a mixed model is likely to be most helpful in these circumstances if there are missing values.
We see this in the estimates of the treatment standard errors. Comparison of Models 1 and 2 for the oedema status shows that the standard errors are identical (to the number of digits reported), indicating that the between-subject variation is so large that recovery of between-subject information is ineffective. With inclusion of the baseline level as a covariate, we see that Model 3 gives the same result as Model 1. This result is well known, showing that a single baseline has no effect on a fixed effects analysis. It does, however, produce a small reduction in the treatment standard error when a mixed model is fitted, showing that some between-subject information has been utilised.
The results for DBP show the recovery of between-subject information more clearly because of the relatively smaller between-subject variation. We see a detectable reduction in the treatment standard error, even when baselines are not used, and with the inclusion of baselines, a reduction of about 4% in the standard error is seen with the mixed models approach. This gain is modest but worthwhile.
The greatest advantage of the mixed models approach will unfortunately be gained in situations where a cross-over trial shows little benefit over a parallel group study, that is where the between-subject variance component is small relative to the residual variance component.
Such a situation occurs in a trial reported by Jones and Kenward (1989). In this two-period, cross-over trial, an oral mouthwash was compared with a placebo mouthwash. There were two 6-week treatment periods, with a 3-week washout period separating them. The outcome variable reported was the average plaque score per tooth, with each tooth being assessed on an integer scale from zero to three. Results were presented for the 34 patients with data from both treatment periods. Interestingly, these data arose from a trial in which 41 patients were randomised, and 38 completed the trial. For the purposes of this illustration, we have deleted the second observation from five randomly selected patients from the 34 with complete data.
Two models were fitted to the data using PROC MIXED. In both, a treatment effect and a period effect were included as fixed. In one, the patient effect was fitted as random, and in the other, it was fitted as fixed. The results are shown in Table 7.3.
Table 7.3 Analysis of oral mouthwash trial.
| Fixed patients | Random patients | |
| Variance components | ||
| Patients | – | 0.029 (0.018) |
| Residual | 0.069 | 0.066 (0.017) |
| Treatment difference (SE) | 0.25 (0.069) | 0.244 (0.065) |
Examination of the variance component terms shows that the patient term is appreciably smaller than the residual term. This indicates that the benefit of employing a cross-over design rather than a parallel group design may be small. The estimate of the period effect (not shown) is small, but in accord with our recommendation in the previous section, we retain it in the model. The main interest, of course, lies in the estimates of the treatment difference and the associated standard errors. Both analyses demonstrate a clear advantage to using the active mouthwash. For our purposes in comparing the results of the two analytical strategies, it is the standard errors that interest us because it is purely a matter of chance which method gives the larger point estimate of the treatment effect. We see that the use of the random effects model has reduced the standard error of the estimate of the treatment difference by about 6%.
SAS code and output
The SAS code to generate analyses for oedema status (Table 7.2) is shown for Models 3 and 4. Models 1 and 2 differ only in the exclusion of the baseline value from the model.
PROC MIXED NOCLPRINT; CLASS treat period patient;
TITLE ‘FIXED EFFECT ANALYSIS WITH BASELINE’;
MODEL oed=treat period patient oedbase;
LSMEANS treat /DIFF PDIFF;
PROC MIXED NOCLPRINT; CLASS treat period patient;
TITLE ‘RANDOM EFFECTS ANALYSIS WITH BASELINE’;
MODEL oed=treat period oedbase / DDFM=KENWARDROGER;
RANDOM patient;
LSMEANS treat /DIFF PDIFF;The output reproduced as follows is from Model 4:
Iteration History | |||
Iteration | Evaluations | -2 Res Log | Criterion |
Likelihood | |||
0 | 1 | 732.30378010 | |
1 | 3 | 620.47659711 | 0.00104614 |
2 | 2 | 620.32698029 | 0.00001998 |
3 | 1 | 620.32375614 | 0.00000001 |
Convergence criteria met | |||
Covariance Parameter | |||
Estimates | |||
Cov Parm | Estimate | ||
patient | 3.7632 | ||
Residual | 0.5260 | ||
Fit Statistics | |||
-2 Res Log Likelihood | 620.3 | ||
AIC (smaller is better) | 624.3 | ||
AICC (smaller is better) | 624.4 | ||
BIC (smaller is better) | 629.4 | ||
Type 3 Tests of Fixed Effects | |||||||
Num | Den | ||||||
Effect | DF | DF | F Value | Pr > F | |||
treat | 1 | 75.3 | 6.79 | 0.0110 | |||
period | 1 | 74.9 | 4.02 | 0.0487 | |||
oedbase | 1 | 94.1 | 1433.62 | <.0001 | |||
Least Squares Means | |||||||
Effect | treat | Estimate | Standard | DF | t Value | Pr > |t| | |
Error | |||||||
treat | A | 55.3621 | 0.2170 | 108 | 255.09 | <.0001 | |
treat | B | 55.0536 | 0.2168 | 107 | 253.90 | <.0001 | |
Differences of Least Squares Means | |||||||
Effect | treat | −treat | Estimate | Standard | DF | t Value | Pr > |t| |
Error | |||||||
treat | A | B | 0.3085 | 0.1184 | 75.3 | 2.61 | 0.0110 |
7.4 Higher order complete block designs
In these designs, there are as many treatment periods as there are treatments to be compared, and each patient receives every treatment. If there are no missing data, then a conventional least squares analysis fitting treatment, period and patient effects is fully efficient. Whenever there are missing data, some of the within-patient treatment comparisons are unavailable for every patient. Therefore, additional between-patient information can be utilised.
7.4.1 Inclusion of carry-over effects
In any cross-over trial, there is the possibility of carry-over effects. That is, the results in second or subsequent treatment periods may be influenced by treatment administered in earlier periods. In the simple two-period, cross-over trial considered previously, there is no possibility of estimating carry-over. In all of the remaining designs considered, carry-over effects can be estimated, and in our examples, we will consider results from models that include carry-over. However, we do this for completeness rather than in the belief that this is good practice, and we return to this point in Section 7.11.
7.4.2 Example: four-period, four-treatment cross-over trial
We consider the four-period, four-treatment cross-over trial described by Jones and Kenward (1989). Three drugs, A, C and D and a placebo B were compared to assess their effect on cardiac output, measured by the left ventricular ejection time (LVET). Each treatment was given for one week, with a one-week washout period between treatments. Observations were made at the end of each treatment period. Fourteen patients were used in the trial, yielding 56 observations. To demonstrate the use of the mixed models approach, we have arbitrarily set 13 of the 56 observations to be missing. The results of four analyses are presented in Table 7.4, from the combinations of inclusion or exclusion of carry-over effects, and handling the patient effects as fixed or random.
Table 7.4 Estimates of variance components and treatment effects. Standard errors of estimates appear in brackets.
| Fixed patients | Random patients | |
| Ignoring carry-over | ||
| Variance components | ||
| Patients | – | 2721 |
| Residual | 1667 | 1657 |
| Treatment differences | ||
| A − B | 77.4 (20.1) | 72.5 (19.9) |
| A − C | 36.8 (17.3) | 32.8 (17.1) |
| A − D | 77.3 (19.5) | 74.6 (19.4) |
| B − C | −40.6 (19.9) | −39.7 (19.5) |
| B − D | −0.1 (21.2) | 2.1 (21.0) |
| C − D | 40.4 (18.7) | 41.8 (18.5) |
| Including carry-over | ||
| Variance components | ||
| Patients | – | 2750 |
| Residual | 1840 | 1831 |
| Treatment differences | ||
| A − B | 76.0 (22.6) | 69.1 (22.2) |
| A − C | 40.5 (20.4) | 32.1 (20.0) |
| A − D | 84.9 (22.5) | 79.0 (22.3) |
| B − C | −35.4 (23.0) | −37.0 (22.4) |
| B − D | 8.9 (25.5) | 9.9 (25.0) |
| C − D | 44.3 (23.0) | 46.9 (22.5) |
All pairwise comparisons of the carry-over effects were non-significant and will not be considered further or the details presented. We see that between-patient variation is moderate, being about 50% higher than the residual variance component. The random effects analysis without carry-over effects produces an average 1% reduction in the standard errors of the paired treatment comparisons compared with the fixed effects model, a modest but worthwhile gain. Comparing these estimates with the analyses in which carry-over was also fitted, two points are clear. Firsly, the standard errors of the mean treatment differences are larger when carry-over terms are present, irrespective of whether a fixed effects model is fitted or whether the patient term is regarded as random. Secondly, the reduction in the standard error of the mean treatment difference by fitting patient effects as random is larger when carry-over terms are also fitted. This latter result is general, and we will see more dramatic differences in later examples.
SAS code and output
/*create dummy variables for carryover effects*/
DATA new; carry=treat; SET mydata; RUN;
DATA new; SET new;
IF period eq 1 THEN carry=4;
* setting a carryover value for the first period.
it is arbitrary which treatment is selected.
the choice will only influence the absolute values
of the fixed effect estimates and not the difference
between them;
PROC MIXED; CLASS treat period patient;
TITLE ‘Fixed Effect Analysis Without Carryover’;
MODEL lvet=treat patient period;
LSMEANS treat/DIFF PDIFF;
PROC MIXED; CLASS treat period patient;
TITLE ‘Random Effects Analysis Without Carryover’;
MODEL lvet=treat period/DDFM=KENWARDROGER;
RANDOM patient;
LSMEANS treat/DIFF PDIFF;
PROC MIXED; CLASS treat period patient carry;
TITLE ‘Fixed Effect Analysis Including Carryover’;
MODEL lvet=treat patient period carry;
LSMEANS treat carry/DIFF PDIFF;
PROC MIXED; CLASS treat period patient carry;
TITLE ‘Random Effects Analysis Including Carryover’;
MODEL lvet=treat period carry/DDFM=KENWARDROGER;
RANDOM patient;
LSMEANS treat carry/DIFF PDIFF;The following output is that generated by the last PROC MIXED procedure.
Random Effects Analysis Including Carryover | |||
The Mixed Procedure | |||
Model Information | |||
Data Set | WORK.NEW | ||
Dependent Variable | lvet | ||
Covariance Structure | Variance Components | ||
Estimation Method | REML | ||
Residual Variance Method | Profile | ||
Fixed Effects SE Method | Prasad-Rao-Jeske- | ||
Kackar-Harville | |||
Degrees of Freedom Method | Kenward-Roger | ||
Class Level Information | |||
Class | Levels | Values | |
treat | 4 | 1 2 3 4 | |
period | 4 | 1 2 3 4 | |
patient | 14 | 1 2 3 4 5 6 7 8 9 10 11 12 13 | |
14 | |||
carry | 4 | 1 2 3 4 | |
Dimensions | |||
Covariance Parameters | 2 | ||
Columns in X | 13 | ||
Columns in Z | 14 | ||
Subjects | 1 | ||
Max Obs Per Subject | 43 | ||
Number of Observations | |||
Number of Observations Read | 43 | ||
Number of Observations Used | 43 | ||
Number of Observations Not Used | 0 | ||
Iteration History | |||
Iteration | Evaluations | -2 Res Log Likelihood | Criterion |
0 | 1 | 390.90717846 | |
1 | 2 | 381.33170184 | 0.00102427 |
2 | 1 | 381.14250906 | 0.00008011 |
3 | 1 | 381.12896819 | 0.00000062 |
4 | 1 | 381.12886806 | 0.00000000 |
Convergence criteria met | |||
Covariance Parameter | ||||||||
Estimates | ||||||||
Cov Parm | Estimate | |||||||
patient | 2749.71 | |||||||
Residual | 1831.47 | |||||||
Fit Statistics | ||||||||
-2 Res Log Likelihood | 381.1 | |||||||
AIC (smaller is better) | 385.1 | |||||||
AICC (smaller is better) | 385.5 | |||||||
BIC (smaller is better) | 386.4 | |||||||
Type 3 Tests of Fixed Effects | ||||||||
Num | Den | |||||||
Effect | DF | DF | F Value | Pr > F | ||||
treat | 3 | 22.3 | 5.59 | 0.0052 | ||||
period | 3 | 21.8 | 3.90 | 0.0226 | ||||
carry | 3 | 23.4 | 0.15 | 0.9316 | ||||
Least Squares Means | ||||||||
Standard | ||||||||
Effect | treat | carry | Estimate | Error | DF | t Value | Pr > |t| | |
treat | 1 | 400.10 | 20.8116 | 27.5 | 19.23 | <.0001 | ||
treat | 2 | 331.02 | 23.0808 | 30.4 | 14.34 | <.0001 | ||
treat | 3 | 367.99 | 20.5018 | 26.8 | 17.95 | <.0001 | ||
treat | 4 | 321.12 | 21.3633 | 29 | 15.03 | <.0001 | ||
carry | 1 | 356.94 | 23.1999 | 31.3 | 15.39 | <.0001 | ||
carry | 2 | 364.74 | 24.3531 | 31.6 | 14.98 | <.0001 | ||
carry | 3 | 350.07 | 27.5438 | 33 | 12.71 | <.0001 | ||
carry | 4 | 348.48 | 21.4910 | 27.5 | 16.22 | <.0001 | ||
Differences of Least Squares Means | ||||||||
Standard | ||||||||
Effect | treat | carry | −treat | −carry | Estimate | Error | DF | t Value |
treat | 1 | 2 | 69.0876 | 22.1976 | 22.5 | 3.11 | ||
treat | 1 | 3 | 32.1188 | 19.9731 | 22.3 | 1.61 | ||
treat | 1 | 4 | 78.9793 | 22.2691 | 21.5 | 3.55 | ||
treat | 2 | 3 | -36.9688 | 22.4442 | 22.6 | -1.65 | ||
treat | 2 | 4 | 9.8917 | 25.0367 | 22.3 | 0.40 | ||
treat | 3 | 4 | 46.8605 | 22.4790 | 22.8 | 2.08 | ||
carry | 1 | 2 | -7.8017 | 25.7917 | 23.6 | -0.30 | ||
carry | 1 | 3 | 6.8688 | 30.4508 | 24.4 | 0.23 | ||
carry | 1 | 4 | 8.4543 | 25.8129 | 21.7 | 0.33 | ||
carry | 2 | 3 | 14.6705 | 28.9287 | 23.2 | 0.51 | ||
carry | 2 | 4 | 16.2560 | 29.1453 | 23.8 | 0.56 | ||
carry | 3 | 4 | 1.5855 | 33.3982 | 25.4 | 0.05 | ||
Differences of Least Squares Means | ||||||||
Effect | treat | carry | −treat | −carry | Pr > |t| | |||
treat | 1 | 2 | 0.0050 | |||||
treat | 1 | 3 | 0.1219 | |||||
treat | 1 | 4 | 0.0019 | |||||
treat | 2 | 3 | 0.1133 | |||||
treat | 2 | 4 | 0.6965 | |||||
treat | 3 | 4 | 0.0485 | |||||
carry | 1 | 2 | 0.7649 | |||||
carry | 1 | 3 | 0.8234 | |||||
carry | 1 | 4 | 0.7464 | |||||
carry | 2 | 3 | 0.6168 | |||||
carry | 2 | 4 | 0.5822 | |||||
carry | 3 | 4 | 0.9625 | |||||
7.5 Incomplete block designs
The previous example demonstrated a situation where we have a design that is intended to be balanced but becomes unbalanced owing to missing observations. In contrast, we now look at incomplete block designs, where the design in itself is unbalanced. They are used in situations where, for practical reasons, the maximum possible number of treatment periods in a cross-over trial is less than the number of treatments to be evaluated, so complete balance is impossible. It is an area we will look at again in Section 8.18. The principal reason for this constraint on the number of treatment periods will usually be the duration for which any patient is in the trial. Some treatments require to be assessed over a period of several weeks, in order for there to be sufficient time for a ‘steady-state’ response to be reached, and so the length of individual treatment periods in the trial can be considerable. In these circumstances, it is not feasible to have multiple treatment periods because of the following reasons.
- The chance that a patient will withdraw before completing the trial protocol increases with the required time in the trial.
- In the programme of testing of a new treatment, excessively long studies will delay drug registration.
- Ethical considerations require that trial participation should not place an excessive burden on the patient.
It is readily seen that fitting a model with fixed patient effects to such a design will be inefficient because it does not allow us to use between-patient information in our treatment comparisons. To demonstrate this, consider a two-period cross-over trial with three treatments, A, B and C. Direct information on the comparison of treatments A and B is given from the within-patient differences in patients receiving both of these treatments. However, taking the random effects approach to modelling patient effects, we can see additionally that the distribution of the sum of the responses in patients receiving treatments A and C, and in those receiving B and C, also yields comparative information about treatments A and B. Thus, the random effects approach allows recovery of between-subject information. Although these designs cannot be completely balanced, they can be partially balanced by ensuring that all possible treatment sequences are used with equal frequency. As long ago as 1940, Yates described a method for recovering between-block information (the patient is the block in cross-over designs) for balanced incomplete block designs, but the benefits of applying this in cross-over studies have not been widely recognised until recently.
7.5.1 Example: Three treatment two-period cross-over trial
Mead (1988) gives results of a two-period cross-over trial to compare three analgesic drugs labelled A, B and C. The trial involved 43 patients in total, and the numbers receiving each treatment combination were as follows: AB 7; BA 5; AC 7; CA 8; BC 8; CB 8. This design is sometimes referred to as ‘Koch’s design’. The effectiveness of each treatment was assessed by the numbers of hours of pain relief provided. The design did not include a washout period between treatments, and so there was a strong possibility of carry-over effects. The model fitted was as follows:
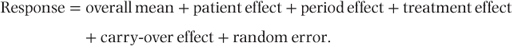
Period, treatment and carry-over effects were taken as fixed. Analyses were carried out with patient effects specified first as fixed in a conventional least squares analysis and then as random in a mixed models analysis.
The estimated variance components and treatments effects are shown in Table 7.5, first omitting and then including carry-over effects. Comparison of the two analyses omitting carry-over effects shows that the average standard error for treatment differences from the combined analysis with recovery of between-patient information is on average 12% less than for the within-patient analysis. The comparison A − B, which has the largest standard error, shows the greatest increase in precision, so that the combined analysis also leads to treatment estimates with a smaller range of standard errors. For this trial, the between-patient component of variance is relatively small, and recovery of between-patient information is clearly worthwhile.
Table 7.5 Estimates of variance components and treatment effects for a cross-over trial comparing three analgesic drugs. Standard errors of estimates appear in brackets.
| Fixed patients | Random patients | |
| Ignoring carry-over | ||
| Variance components | ||
| Patients | – | 1.3 |
| Units within patients | 10.8 | 10.7 |
| Treatment effects | ||
| A − B | 3.4 (1.05) | 3.5 (0.91) |
| A − C | 2.0 (0.99) | 1.9 (0.88) |
| B − C | −1.4 (0.98) | −1.6 (0.87) |
| Including carry-over | ||
| Variance components | ||
| Patients | – | 1.3 |
| Units within patients | 11.3 | 10.9 |
| Treatment effects | ||
| A − B | 3.7 (2.01) | 3.8 (0.99) |
| A − C | 2.6 (2.14) | 1.9 (0.99) |
| B − C | −1.1 (2.08) | −1.9 (0.99) |
| Carry-over effects | ||
| A − B | 0.4 (3.43) | 1.0 (1.45) |
| A − C | 1.1 (3.66) | 0.2 (1.41) |
| B − C | 0.7 (3.72) | −0.8 (1.46) |
Although the estimated carry-over effects are generally small relative to their standard errors, the results from this model could be preferred on the basis of the trial design and the absolute magnitude of the estimated carry-over effects. With this model, we see that the magnitudes of the standard errors of the treatment effects using a mixed model are only half of those obtained from the fixed effects model. The standard errors of the carry-over effects show an even greater separation. Using the mixed models approach, the penalty in fitting carry-over terms is an increase of just over 10% in the standard errors of the treatment differences.
For this trial, the between-patient variance component is small compared with the within-patient component (γ = 0.12), suggesting that there is little advantage in using a cross-over trial for testing these analgesics, even if carry-over effects can be avoided. Indeed, the predicted average standard error for treatment comparisons for a parallel group trial with the same number of patient sessions per treatment is 0.92, compared with 0.89 and 0.99 for the cross-over analysis ignoring and including carry-over effects, respectively.
SAS code and output
This is similar to that of the earlier examples and is omitted.
7.6 Optimal designs
There has been substantial research into cross-over designs in which estimates of treatment effects and carry-over effects are both of interest. As indicated earlier in this chapter, we would question whether such an approach is likely to be desirable in clinical trials, though it may prove useful in applications in agriculture. However, for various combinations of numbers of treatments, and numbers of treatment periods, the so-called optimal designs have been derived. They satisfy the property of giving uniformly most powerful unbiased estimates of treatment and carry-over effects.
One particular optimal design has been used in practice and arguably has a stronger justification for its use than the other optimal designs. This is Balaam’s design for the situation of two treatments and two treatment periods. Of course, the most common design for this situation is not Balaam’s design but the simple AB/BA design. However, its critics would argue that a weakness is its inability to estimate carry-over effects and simultaneously use data from the second period in estimating treatment effects. Balaam’s design resolves the problem by employing all four possible treatment sequences – AA, BB, AB and BA.
7.6.1 Example: Balaam’s design
This is a well-known example initially described by Hunter et al. (1970). The aim was to determine the effect of amantadine (treatment A) on subjects with Parkinsonism. The trial was placebo controlled (treatment B). After a run-in period of 1 week during which baseline information was recorded, there were two 4-weekly treatment periods, without a washout period. Weekly scores (0–4) were recorded for each of 11 physical signs, and the data presented in Table 7.6 give the weekly average total scores in each treatment period. Seventeen patients were randomised, and the data have no missing values.
Table 7.6 Average scores for amantadine trial.
| Group | Subject | Baseline | Period 1 | Period 2 |
| 1AA | 1 | 14 | 12.50 | 14.00 |
| 2 | 27 | 24.25 | 22.50 | |
| 3 | 19 | 17.25 | 16.25 | |
| 4 | 30 | 28.25 | 29.75 | |
| Mean | 22.50 | 20.56 | 20.63 | |
| 2BB | 1 | 21 | 20.00 | 19.51 |
| 2 | 11 | 10.50 | 10.00 | |
| 3 | 20 | 19.50 | 20.75 | |
| 4 | 25 | 22.50 | 23.50 | |
| Mean | 19.25 | 18.13 | 18.44 | |
| 3AB | 1 | 9 | 8.75 | 8.75 |
| 2 | 12 | 10.50 | 9.75 | |
| 3 | 17 | 15.00 | 18.50 | |
| 4 | 21 | 21.00 | 21.50 | |
| Mean | 14.75 | 13.81 | 14.63 | |
| 4BA | 1 | 23 | 22.00 | 18.00 |
| 2 | 15 | 15.00 | 13.00 | |
| 3 | 13 | 14.00 | 13.75 | |
| 4 | 24 | 22.75 | 21.50 | |
| 5 | 18 | 17.75 | 16.75 | |
| Mean | 18.60 | 18.30 | 16.60 |
Table 7.7 presents the results of analyses with and without inclusion of a carry-over term and with patient effects fitted as fixed or random.
Table 7.7 Estimates of variance components and treatment effects. Standard errors of estimates appear in brackets.
| Fixed patients | Random patients | |
| Ignoring carry-over | ||
| Variance components | ||
| Patients | – | 30.3 |
| Residual (within patients) | 1.05 | 1.1 |
| Treatment difference | 1.29 (0.49) | 1.24 (0.48) |
| Including carry-over | ||
| Variance components | ||
| Patients | – | 30.5 |
| Residual (within patients) | 1.12 | 1.1 |
| Treatment difference | 1.42 (0.73) | 1.28 (0.70) |
| Carry-over difference | 0.25 (1.06) | 0.10 (0.92) |
An immediate point to note from the two mixed models is the very high patient variance component compared with the residual variance component (Table 7.8). This immediately suggests that little gain in efficiency will accrue from between-patient information. This is confirmed by comparison of the treatment standard errors, where even in the model in which carry-over is fitted, the reduction is only 4%. In most situations, where the between-patient variation is less extreme, the existence of the AA and BB treatment groups would lead us to expect greater benefits from the mixed models approach.
In this study, there is no evidence of any carry-over effect, and most statisticians would choose to report the model that excludes carry-over. However, having chosen a design for its optimal properties in estimating both treatment and carry-over effects, there is a strong case for reporting the fuller model.
The presentation in this example has been restricted to the analysis of the results in the two treatment periods, and the fact that baseline observations were also recorded has been ignored. Jones and Kenward (1989) present additional analyses utilising this baseline data, and, in particular, use interactions with the baseline to test for an effect of the baseline level on the treatment effect, period effect and carry-over effect. Although none of these terms was statistically significant at the 10% level of significance, they found indications that the treatment differences were higher with greater baseline levels. These authors also handled carry-over in a more involved way than we have employed in our analyses. They allowed for the possibility that carry-over would be different in those on the AA or BB sequence from those on the AB or BA sequence, but this term in the analysis of variance was clearly non-significant.
The conclusions from the trial will, in this instance, be qualitatively similar whichever of the previously described analytical methods is used, as long as carry-over is ignored in estimating treatment effects. Amantadine produces a reduction in the physical signs of Parkinson’s disease, which is statistically significant at the 5% level. Note, however, that inclusion of carry-over terms in the model produces a substantial increase in the standard error of the treatment effect, leading to non-significance of the treatment effect.
SAS code and output
The SAS code and the structure of the output are almost identical to that presented at the end of Section 7.4, except that two treatments are used instead of four. The key results are tabulated in Table 7.7.
7.7 Covariance pattern models
In the examples considered so far in this chapter, the mixed models approach has fitted the patient effects as random. As we have seen earlier, this implies that the observations within one patient are all assumed to have the same correlation and variance. However, it could be argued that in trials with three or more periods, the correlation may vary with different pairs of periods. In particular, periods that were closer together might be expected to show higher correlations. In this section, we explore the situation where the covariance patterns used are ‘structured’.
7.7.1 Structured by period
This is perhaps the most obvious way to structure the residual covariance matrix. We have already mentioned the possibility that periods close together in time might have a higher correlation than those far apart in time. In addition, it is possible that the residual variance may itself change over successive periods. For example, in early periods of the trial, while the protocol is unfamiliar to patients, the observations may be more variable than in later periods. We have already seen that SAS offers a wide choice of covariance patterns, and so a strategy for investigating alternatives is preferable to a blunderbuss approach of examining the full range available. A comparison of the compound symmetry structure (equivalent to simply fitting patient effects as random) and the general covariance matrix will usually be helpful in determining whether use of a more complicated covariance structure is likely to be useful. We will explore this further in the forthcoming example.
Table 7.8 Comparison of covariance pattern models for the four-way cross-over trial, with inclusion of carry-over effects.
| Covariance pattern | Period/ treatment | Variances (×102) | Correlations | − 2 log likelihood (no. of parameters) | Estimated treatment differences (model-based SE) | Estimated carry-over differences (model-based SE) |
| Compound symmetry | 1–4 | 36 |  | 519.2 (2) |  | 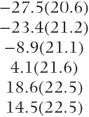 |
| General (across periods) |  |  |  | 502.2 (10) |  | 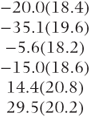 |
| General (across treatments) |  | 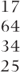 | 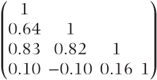 | 498.0 (10) |  |  |
7.7.2 Structured by treatment
Although structuring by period is the most obvious way of introducing structure, this can also be applied to treatments. In parallel group trials, we have already met situations where we might wish to fit separate variances for each of the treatment groups. There is an exact analogy in the cross-over situation, where the variances may differ for some of the treatments. In addition, there may be good reason to suspect that the results from certain pairs of treatments may be more highly correlated than others if they have a similar mode of action. Thus, a more complicated structure for treatments than the simple compound symmetry may be highly plausible. This type of approach has been found to be particularly useful in the analysis of bioequivalence trials where treatment differences in reproducibility are highly relevant; examples of its application are available on the FDA website (www.fda.gov). We also present an example in Section 8.15.
7.7.3 Example: four-way cross-over trial
We will consider the four-way cross-over trial analysed in Section 7.4, which compared the effects of three drugs A, C and D and a placebo B on blood flow. This time, no values are set to missing, and therefore the study is more balanced (across random effects). Each treatment period lasted a week and was followed by a washout period also lasting a week. An analysis fitting a random effects model (i.e. a compound symmetry pattern) is compared with analyses fitting general covariance matrices. The covariance matrix is first structured according to periods and then according to treatments. Treatment and period effects are fitted as fixed effects in each analysis. In the first instance, we also include a carry-over effect as an additional fixed effect in the analysis.
Examination of the second model in Table 7.8 shows that data are more variable in the first period than in other periods. This is a common occurrence in clinical trials and is one reason why a run-in period is often used. The correlations between periods indicate a tendency for more widely separated periods to have lower correlations than those close together. The third model shows a higher variation for the placebo treatment (B) than for the three active treatments. Interestingly, the correlations involving treatment D are substantially lower than the correlation between treatments A, B and C.
Table 7.9 Comparison of covariance pattern models for the four-way cross-over trial, without carry-over effects.
| Error model | Period/ treatment | Variances (×102) | Correlations | − 2 log likelihood (no. of parameters) | Estimated treatment differences (model SE) |
| Compound symmetry | 1–4 | 36 |  | 544.6 (2) |  |
| General (across periods) | 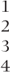 | 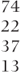 |  | 528.2 (10) |  |
| General (across treatments) | 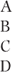 | 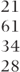 |  | 527.4(10) |  |
Both general covariance models show significant improvements over the compound symmetry model when tested by likelihood ratio tests (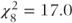 , p = 0.03 and
, p = 0.03 and 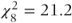 , p = 0.007) and might therefore be preferred.
, p = 0.007) and might therefore be preferred.
A comparison of the three models with respect to the estimates of treatment differences shows that the estimates vary substantially when treatment C is involved. The same comment applies when the carry-over effects are compared.
Tests of the null hypothesis of equal treatment effects are all highly significant whichever model is used. For the compound symmetry model, the p-value is 0.003 compared with 0.005 for each of structuring by period and structuring by treatment.
The tests for equality of carry-over effects are more dependent on the choice of model, though none is statistically significant at conventional levels. The three models yield p-values of 0.54, 0.35 and 0.19.
All three models would therefore produce similar overall conclusions with respect to the presence of significant treatment differences without evidence of carry-over. Every model estimates the greatest levels of LVET with treatment A, followed by treatments C, B and D. The conclusions in respect of particular pairs of treatments would depend, however, on the model selected. On the basis of the likelihoods, the model employing structuring by treatment might be preferred, leading to a conclusion of similar higher levels of LVET for treatments A and C, with treatments B and D at similar lower levels. One would also conclude that results with treatment D were only weakly correlated with results on other treatments, which in turn are quite highly correlated.
In view of the absence of any significant carry-over in any of the models, it would seem reasonable to go on to consider models in which carry-over is omitted. We would advocate this even if the above model had demonstrated significant carry-over for reasons that are elaborated upon in Section 7.11. We note for the moment that this trial used reasonable washout periods, making physical carry-over of drugs unlikely, and that even if carry-over does occur, the simple carry-over model used may be inappropriate.
The use of the same three covariance structures as before, but without carry-over in the model, is summarised in Table 7.9. Many of the comments made on the previous models still apply. The patterns of covariances are similar, and structuring by period or by treatment produces a significant increase in the likelihoods compared with the compound symmetry pattern. All of the models give similar estimates of the treatment differences, which do not involve treatment C. The estimates involving treatment C are similar for the compound symmetry model and for the structured-by-treatment model but are substantially different with structuring by period. In view of the highest likelihood being obtained when structuring by treatment and the consistency of the estimates when compared with the compound symmetry model, this model might be tentatively accepted.
As noted in the corresponding model when carry-over was included, the correlations involving treatment D are relatively low. This treatment is also the one producing the lowest measurements. This may therefore increase further the plausibility of this model, suggesting as it does a different but less effective form of action.
All of the above results have been obtained using the Kenward–Roger option to correct for the fixed effects standard error bias. In many situations, this bias has been small in comparison with the use of the Satterthwaite option, but in this example, it is occasionally large. In the models in which we structure by periods, the standard errors of the treatment differences are over 30% larger using the Kenward–Roger option. In some other models, the influence is marginal. Further details can be obtained by comparison with the corresponding table in the first edition of this book for which the Kenward–Roger option was unavailable. We believe that use of the Kenward–Roger option is the correct approach, and there is indirect support for this view by consideration of the standard errors across the different models. Their variation is relatively small, and this compares with the substantial variation seen with other approaches. In the first edition, we also reported the ‘empirical’ standard errors (see Section 2.4.3) and raised questions of their validity in this context. For all but one of the 18 treatment comparisons in Table 7.9, the empirical standard errors are less than the Kenward–Roger standard error, and sometimes the inconsistency is gross. For example, the empirical standard error of C − D in the structured-by-period model is only 4.6 compared with 11.2 for the model-based standard error and 14.8 for the Kenward–Roger standard error. We therefore see no place for the use of unadjusted empirical standard errors with normally distributed, repeated measures data in relatively small datasets. The role of empirical standard errors with non-normal data and the adequacy of the corrections to the empirical standard errors available in PROC GLIMMIX are still an under-researched area.
Returning to the consideration of our findings in Tables 7.8 and 7.9, we believe that there is a case for basing our inferences on the model without carry-over, with the covariances being structured by treatment. Choosing the model from which to present findings is not always straightforward, however. Decisions concerning the inclusion of carry-over terms may be based primarily on how the trial was designed and, in particular, on the adequacy of washout periods. The choice between different covariance pattern models may be influenced by consideration of the likelihoods. However, statistical tests need not be the only factor determining model choice. The validity of the assumptions relating to a model is also important. For example, if we believe that periods and treatments are unlikely to have varying correlations based on past experience or if the trial is too small to give precise covariance estimates, then a compound symmetry structure possibly may be the one of choice.
It will always be a cause for concern when different models give qualitatively different conclusions, and this is always a greater danger when the data are relatively sparse. The different conclusions that were reached with different models and different approaches to the calculation of standard errors that we reported previously have, however, been resolved with the correction of the fixed effects standard error bias using the Kenward–Roger method.
This example makes the point that treating a multi-period, cross-over trial as repeated measures data with a covariance pattern that is structured by treatment provides an additional approach to analysis, which can be informative. For analyses that are conducted in the pharmaceutical industry for drug registration purposes, the requirement to specify the analysis plan in the trial protocol may be restrictive. This is likely to cause the compound symmetry model to be the one of choice for a primary analysis. It should be acceptable, though, to specify a secondary analysis that is structured by treatment, so that the interrelationships of responses to different treatments can be explored.
SAS code and output
The following code uses the same variable names specified at the end of Section 7.4. The code is given as follows initially for the compound symmetry model, with inclusion of carry-over effects.
PROC MIXED; CLASS treat period patient carry;
TITLE ‘COMPOUND SYMMETRY’;
MODEL lvet=treat period carry/ DDFM=KENWARDROGER;
REPEATED period/ SUBJECT=patient TYPE=CS RCORR;
LSMEANS treat carry/DIFF PDIFF;The code for the other covariance pattern models is identical except for the REPEATED statement.
TITLE ‘STRUCTURED BY PERIOD’;
REPEATED period/ SUBJECT=patient TYPE=UN RCORR;
TITLE ‘STRUCTURED BY TREATMENT’;
REPEATED treat/ SUBJECT=patient TYPE=UN RCORR;The changes to remove carry-over effects are obvious. The following output is for the example where structuring by treatment is employed.
STRUCTURED BY TREATMENT | |||
The Mixed Procedure | |||
Model Information | |||
Data Set | WORK.NEW | ||
Dependent Variable | lvet | ||
Covariance Structure | Unstructured | ||
Subject Effect | patient | ||
Estimation Method | REML | ||
Residual Variance Method | None | ||
Fixed Effects SE Method | Prasad-Rao-Jeske- | ||
Kackar-Harville | |||
Degrees of Freedom Method | Kenward-Roger | ||
Class Level Information | |||
Class | Levels | Values | |
treat | 4 | 1 2 3 4 | |
period | 4 | 1 2 3 4 | |
patient | 14 | 1 2 3 4 5 6 7 8 9 10 11 12 13 | |
14 | |||
carry | 4 | 1 2 3 4 | |
Dimensions | |||
Covariance Parameters | 10 | ||
Columns in X | 13 | ||
Columns in Z | 0 | ||
Subjects | 14 | ||
Max Obs Per Subject | 4 | ||
Number of Observations | |||
Number of Observations Read | 56 | ||
Number of Observations Used | 56 | ||
Number of Observations Not Used | 0 | ||
Iteration History | |||
Iteration | Evaluations | -2 Res Log Likelihood | Criterion |
0 | 1 | 531.19328518 | |
1 | 2 | 508.00614950 | 0.02010791 |
2 | 1 | 502.46576070 | 0.01043261 |
3 | 1 | 499.65259977 | 0.00468615 |
4 | 1 | 498.42652859 | 0.00154375 |
5 | 1 | 498.03992412 | 0.00028985 |
6 | 1 | 497.97162927 | 0.00002064 |
7 | 1 | 497.96709658 | 0.00000023 |
8 | 1 | 497.96704876 | 0.00000000 |
Convergence criteria met | |||
Estimated R Correlation Matrix | ||||
for patient 1 | ||||
Row | Col1 | Col2 | Col3 | Col4 |
1 | 1.0000 | 0.6367 | 0.8333 | 0.09861 |
2 | 0.6367 | 1.0000 | 0.8184 | -0.09949 |
3 | 0.8333 | 0.8184 | 1.0000 | 0.1628 |
4 | 0.09861 | -0.09949 | 0.1628 | 1.0000 |
Covariance | ||||
Parameter Estimates | ||||
Cov Parm | Subject | Estimate | ||
UN(1,1) | patient | 1681.02 | ||
UN(2,1) | patient | 322.45 | ||
UN(2,2) | patient | 6360.25 | ||
UN(3,1) | patient | 390.80 | ||
UN(3,2) | patient | 3891.90 | ||
UN(3,3) | patient | 3429.52 | ||
UN(4,1) | patient | -205.26 | ||
UN(4,2) | patient | 2555.15 | ||
UN(4,3) | patient | 2411.65 | ||
UN(4,4) | patient | 2531.98 | ||
Fit Statistics | ||||
-2 Res Log Likelihood | 498.0 | |||
AIC (smaller is better) | 518.0 | |||
AICC (smaller is better) | 524.3 | |||
BIC (smaller is better) | 524.4 | |||
Null Model Likelihood | ||||
Ratio Test | ||||
DF | Chi-Square | Pr > ChiSq | ||
9 | 33.23 | 0.0001 | ||
Type 3 Tests of Fixed Effects | ||||
Num | Den | |||
Effect | DF | DF | F Value | Pr > F |
treat | 3 | 10.3 | 7.75 | 0.0054 |
period | 3 | 11 | 8.91 | 0.0028 |
carry | 3 | 14.1 | 1.82 | 0.1890 |
Least Squares Means | ||||||||
Standard | ||||||||
Effect | treat | carry | Estimate | Error | DF | t Value | Pr > |t| | |
treat | 1 | 388.46 | 11.5910 | 13.4 | 33.51 | <.0001 | ||
treat | 2 | 344.64 | 21.7665 | 12.8 | 15.83 | <.0001 | ||
treat | 3 | 380.15 | 17.9227 | 16.2 | 21.21 | <.0001 | ||
treat | 4 | 322.10 | 13.9013 | 10.8 | 23.17 | <.0001 | ||
carry | 1 | 338.38 | 16.3402 | 21.4 | 20.71 | <.0001 | ||
carry | 2 | 361.92 | 18.4008 | 23.7 | 19.67 | <.0001 | ||
carry | 3 | 392.39 | 21.0386 | 33.6 | 18.65 | <.0001 | ||
carry | 4 | 342.66 | 15.5753 | 19.2 | 22.00 | <.0001 | ||
Differences of Least Squares Means | ||||||||
Standard | ||||||||
Effect | treat | carry | −treat | −carry | Estimate | Error | DF | t Value |
treat | 1 | 2 | 43.8265 | 23.5349 | 12.4 | 1.86 | ||
treat | 1 | 3 | 8.3143 | 19.2337 | 12.1 | 0.43 | ||
treat | 1 | 4 | 66.3686 | 18.8818 | 9.8 | 3.51 | ||
treat | 2 | 3 | -35.5123 | 14.4029 | 13.3 | -2.47 | ||
treat | 2 | 4 | 22.5421 | 18.1408 | 14.1 | 1.24 | ||
treat | 3 | 4 | 58.0543 | 13.2261 | 15.3 | 4.39 | ||
carry | 1 | 2 | -23.5450 | 18.7010 | 17 | -1.26 | ||
carry | 1 | 3 | -54.0162 | 22.6449 | 17.6 | -2.39 | ||
carry | 1 | 4 | -4.2811 | 16.4810 | 7.98 | -0.26 | ||
carry | 2 | 3 | -30.4712 | 21.5069 | 17 | -1.42 | ||
carry | 2 | 4 | 19.2639 | 21.4383 | 11.6 | 0.90 | ||
carry | 3 | 4 | 49.7351 | 24.6643 | 30.2 | 2.02 | ||
Differences of Least Squares Means | ||||||||
Effect | treat | carry | −treat | −carry | Pr > |t| | |||
treat | 1 | 2 | 0.0864 | |||||
treat | 1 | 3 | 0.6731 | |||||
treat | 1 | 4 | 0.0058 | |||||
treat | 2 | 3 | 0.0280 | |||||
treat | 2 | 4 | 0.2343 | |||||
treat | 3 | 4 | 0.0005 | |||||
carry | 1 | 2 | 0.2250 | |||||
carry | 1 | 3 | 0.0286 | |||||
carry | 1 | 4 | 0.8016 | |||||
carry | 2 | 3 | 0.1747 | |||||
carry | 2 | 4 | 0.3871 | |||||
carry | 3 | 4 | 0.0527 | |||||
7.8 Analysis of binary data
The earlier sections in this chapter have considered trials where the response variable was assumed to be normally distributed. Although these types of data are almost certainly the most common, binary data are by no means unusual. We have seen in Chapter 3 how the mixed models approach can be extended from normally distributed data to binary data using generalised linear mixed models. The approach described in that chapter can be used for any of the designs considered earlier in this chapter, but we will restrict ourselves to examining the simplest, and probably most common, cross-over design: the AB/BA design.
We utilise an example presented by Jones and Kenward (1989), with deletion of some observations in the second treatment period. The sample comes from safety data from a trial on cerebrovascular insufficiency. The response variable was whether an electrocardiogram was assessed by a cardiologist to be normal (1) or abnormal (0). The modified data are presented in Table 7.10.
Table 7.10 Data from an AB/BA trial on cerebrovascular deficiency. Outcomes 0 and 1 correspond to abnormal and normal ECG readings with deleted observations denoted by •.
| Outcomes | |||||||
| Sequence | (0, 0) | (0, 1) | (0, •) | (1, 0) | (1, 1) | (1, •) | Total |
| AB | 11 | 1 | 2 | 6 | 27 | 3 | 50 |
| BA | 12 | 5 | 2 | 5 | 23 | 3 | 50 |
| Total | 23 | 6 | 4 | 11 | 50 | 6 | 100 |
In a fixed effects analysis, those subjects with a missing observation do not contribute to the evaluation of treatment effects. Testing the null hypothesis of no treatment difference can be performed most powerfully using Prescott’s test (Prescott, 1981). This requires reorganisation of the data in Table 7.10 to the form in Table 7.11 where the rows can be thought of as representing a ‘change score’ from period 1 to period 2, with values –1, 0 or 1.
Table 7.11 Data from Table 7.10 reorganised in form for the application of Prescott’s test.
| Change score | ||||
| Sequence | − 1 | 0 | 1 | Total |
| AB | 1 | 38 | 6 | 45 |
| BA | 5 | 35 | 5 | 45 |
| Total | 6 | 73 | 11 | 90 |
Values of this change score are then compared between the treatment sequence groups. This is undertaken most appropriately using an exact trend test (which is equivalent to a permutation t test). Within SAS, this can be achieved using an EXACT option within PROC FREQ. It yields a p-value of 0.33 (the corresponding asymptotic test gives p = 0.22).
A problem with this approach is that it is based purely on significance testing. It does not yield an estimate of the magnitude of the treatment effect. The use of a mixed model allows us to both recover the between-patient information and obtain meaningful estimates of the magnitude of the treatment effect.
As discussed in Sections 3.2.3 and 3.3.2, problems caused by uniform random effects categories are likely to arise if patients are fitted as random, since there are only two observations per patient. This can be avoided by using instead a covariance pattern model with a compound symmetry structure. The SAS code and most relevant parts of the output are presented at the end of this section.
The correlation parameter estimate is 0.59 and indicates that observations on the same patient are quite strongly correlated.
The estimate of the period effect (0.19) is similar to its standard error (0.20) and is therefore clearly non-significant. It is not negligible, however, and we repeat our recommendation that the period effect should always be included in the model.
The treatment estimate of − 0.32 with 95% confidence limits from − 0.71 to 0.07 corresponds to the estimate on the logistic scale. By exponentiating these figures, we obtain a point estimate and 95% confidence intervals for the odds ratio (i.e. a ratio of proportion normal to proportion abnormal in the two treatment groups). This gives an estimated odds ratio of 0.73, with 95% confidence limits of 0.49–1.07.
Note that this confidence interval was obtained using the MODELSE option in PROC GENMOD to give the model-based variance estimator. The default given is the empirical variance estimator. If empirical variance estimators are used, the 95% confidence interval is slightly narrower, but only the third decimal place is affected (these results obtained from Version 9 of SAS differ slightly from those in the first edition of this book, based on Version 6. The previous computational method can be used by specifying V6CORR as an option in the REPEATED statement.)
Although we should not be unduly influenced by single examples, we note that the significance level obtained for the treatment effect in this analysis was p = 0.10 using the empirical variance estimator and p = 0.11 with the model-based variance estimator compared with p = 0.33 for Prescott’s test. The ability of the model to recover information from patients with incomplete data, together with its capacity to provide meaningful estimates of treatment effects, should make it the preferred option. This latter feature means that it may also be preferred when data are complete. When data are complete, treatment estimates can also be obtained via a bivariate logistic model proposed by Jones and Kenward (1989). They differ, however, from those provided by the mixed models approach. The odds ratio that they produce is conditional on different responses being observed in the two treatment periods. Thus, they report an odds ratio of 0.0385 on the complete data from which our example was derived. Senn (2002) has also suggested a method based on applying ordinal logistic regression techniques to the data as configured in Table 7.11. This method yields yet another different estimate of a treatment effect in the form of an odds ratio. Our initial examination of this method suggests that it is less powerful than the alternatives considered, and we do not consider it further. The estimate from the mixed model provides, we believe, a natural, comprehensible estimate and is our recommendation for all cases where confidence interval estimates are required for the magnitude of the treatment effect. Note, however, that it is based on asymptotic theory, and the values from small studies must be regarded as approximate.
SAS code and output
PROC GENMOD;
CLASS treat period patient;
MODEL outcome/one=period treat/ ERROR=B;
REPEATED SUBJECT=patient/ WITHIN=period TYPE=CS MODELSE CORRW;The GENMOD Procedure | ||
Model Information | ||
Data Set | WORK.A | |
Distribution | Binomial | |
Link Function | Logit | |
Response Variable (Events) | outcome | |
Response Variable (Trials) | one | |
Number of Ob servations Read | 200 | |
Number of Observations Used | 190 | |
Number of Events | 125 | |
Number of Trials | 190 | |
Missing Values | 10 | |
Class Level Information | ||
Class | Levels | Values |
treat | 2 | A B |
period | 2 | 1 2 |
patient | 100 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | ||
38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | ||
55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 | ||
72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 | ||
… | ||
Parameter Information | |||
Parameter | Effect | treat | period |
Prm1 | Intercept | ||
Prm2 | period | 1 | |
Prm3 | period | 2 | |
Prm4 | treat | A | |
Prm5 | treat | B | |
Criteria For Assessing Goodness Of Fit | |||
Criterion | DF | Value | Value/DF |
Deviance | 187 | 242.0829 | 1.2946 |
Scaled Deviance | 187 | 242.0829 | 1.2946 |
Pearson Chi-Square | 187 | 189.9881 | 1.0160 |
Scaled Pearson X2 | 187 | 189.9881 | 1.0160 |
Log Likelihood | -121.0414 | ||
Algorithm converged.
Analysis Of Initial Parameter Estimates | ||||||||
Standard | Wald | 95% | Chi- | |||||
Parameter | DF | Estimate | Error | Confidence | Limits | Square | Pr > ChiSq | |
Intercept | 1 | 0.8128 | 0.2752 | 0.2734 | 1.3522 | 8.72 | 0.0031 | |
period | 1 | 1 | 0.1146 | 0.3077 | -0.4884 | 0.7177 | 0.14 | 0.7095 |
period | 2 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
treat | A | 1 | -0.4233 | 0.3082 | -1.0273 | 0.1808 | 1.89 | 0.1696 |
treat | B | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
Scale | 0 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | |||
NOTE: The scale parameter was held fixed.
As in the example considered in Section 6.4, the above output will always be produced, but it is irrelevant.
GEE Model Information | |
Correlation Structure | Exchangeable |
Within-Subject Effect | period (2 levels) |
Subject Effect | patient (100 levels) |
Number of Clusters | 100 |
Clusters With Missing Values | 10 |
Correlation Matrix Dimension | 2 |
Maximum Cluster Size | 2 |
Minimum Cluster Size | 1 |
Algorithm converged.
Working Correlation Matrix | |||||||
Col1 | Col2 | ||||||
Row1 | 1.0000 | 0.5851 | |||||
Row2 | 0.5851 | 1.0000 | |||||
Exchangeable Working | |||||||
Correlation | |||||||
Correlation | 0.5850903245 | ||||||
Analysis Of GEE Parameter Estimates | |||||||
Empirical Standard Error Estimates | |||||||
Standard | 95% Confidence | ||||||
Parameter | Estimate | Error | Limits | Z | Pr > |Z| | ||
Intercept | 0.6842 | 0.2484 | 0.1973 | 1.1712 | 2.75 | 0.0059 | |
period | 1 | 0.1901 | 0.1976 | -0.1972 | 0.5774 | 0.96 | 0.3360 |
period | 2 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
treat | A | -0.3213 | 0.1979 | -0.7091 | 0.0665 | -1.62 | 0.1044 |
treat | B | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
Analysis Of GEE Parameter Estimates | |||||||
Model-Based Standard Error Estimates | |||||||
Standard | 95% Confidence | ||||||
Parameter | Estimate | Error | Limits | Z | Pr > |Z| | ||
Intercept | 0.6842 | 0.2418 | 0.2103 | 1.1581 | 2.83 | 0.0047 | |
period | 1 | 0.1901 | 0.2001 | -0.2020 | 0.5822 | 0.95 | 0.3419 |
period | 2 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
treat | A | -0.3213 | 0.2004 | -0.7140 | 0.0715 | -1.60 | 0.1089 |
treat | B | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
Scale | 1.0013 | . | . | . | . | . | |
NOTE: The scale parameter for GEE estimation was computed as the square root of the normalized Pearson’s chi-square.
7.9 Analysis of categorical data
Apart from the case of binary data, response variables that are purely categorical, without an underlying scale, are extremely rare. We will therefore only consider data on ordinal scales in this section. Variables classified as none, mild, moderate and severe will arise in a variety of contexts.
To illustrate techniques, we will again take an example from Jones and Kenward (1989) and delete five observations from the second treatment period. The example is a placebo-controlled trial of a treatment for primary dysmenorrhoea. Thirty patients entered the trial, and in each treatment period, the amount of relief obtained was recorded as none or minimal (1), moderate (2) and complete (3). The data as we analyse them are summarised in Table 7.12.
Table 7.12 Data from an AB/BA trial on a treatment for primary dysmenorrhoea (A: placebo; B: high-dose analgesic; deleted observations in the second period denoted by •).
| Sequence | (1, 1) | (1, 2) | (1, 3) | (1, •) | (2, 1) | (2, 2) | (2, 3) | (2, •) | (3, 1) | (3, •) | Total |
| AB | 2 | 3 | 5 | 1 | 1 | 1 | 2 | 1 | 0 | 0 | 16 |
| BA | 3 | 2 | 0 | 0 | 1 | 0 | 1 | 1 | 4 | 2 | 14 |
| Total | 5 | 5 | 5 | 1 | 2 | 1 | 3 | 2 | 4 | 2 | 30 |
| Change score | |||||||||||
| Sequence | − 2 | − 1 | 0 | 1 | 2 | Total | |||||
| AB | 5 | 5 | 3 | 1 | 0 | 14 | |||||
| BA | 0 | 3 | 3 | 1 | 4 | 11 | |||||
| Total | 5 | 8 | 6 | 2 | 4 | 25 | |||||
Taking a fixed effects approach, a test of significance is most readily obtained using methods based on the analysis of an appropriate contingency table. A simple but inefficient way of producing such a contingency table would be to categorise the changes in the outcome variable from the first treatment period to the second as ‘worse’, ‘no change’ and ‘better’ and to tabulate this variable against the treatment sequence. The significance of the treatment effect could then be determined from this 3 × 2 contingency table, as in Prescott’s test. However, this configuration does not use the information that observations of ‘none’ and ‘complete’ in the two treatment periods represent a larger difference than between ‘none’ and ‘moderate’ or ‘moderate’ and ‘complete’. If we arbitrarily assign numbers of 1, 2 and 3 to the outcome categories, we can generate a 5 × 2 contingency table based on the change scores. The ‘obvious’ approach is to then apply a permutation t test (test for trend) to this table to assess the significance of the treatment effect. Application to the change scores presented in Table 12 gives p = 0.005.
In applying this test, it should be appreciated that the scores of − 2, − 1, 0, + 1 and + 2 are arbitrary. They should not be taken to imply that the difference between ‘none’ and ‘complete’ is twice as large as the difference between ‘none’ and ‘moderate’ nor that the difference between ‘none’ and ‘moderate’ is the same as that between ‘moderate’ and ‘complete’. For this reason, some statisticians may wish to replace the change scores with ranks and apply an (exact) Wilcoxon rank sum test. The choice will rarely make any practical difference, but it is clearly good practice to make this choice prior to analysis, rather than reporting the more favourable result. Note that the situation becomes more complicated when there are more than three categories for the outcome variable. Analysis could still be based on the change scores, but there would be an implicit strong assumption about the meaning of the intervals between the categories. Without such strong assumptions, many of the categories of change would be indistinguishable from each other, and a simplified 5 × 2 contingency table would result. Such an example is presented by Senn (2002).
The mixed models approach with random patient effects and fixed period and treatment effects, based on carrying out ordinal logistic regression, is now available through PROC GLIMMIX. The patient variance component is, surprisingly for a cross-over trial, estimated to be negative and therefore set to zero. The coefficient for the treatment effect, on the logistic scale, is 1.92, with a standard error of 0.57 (p = 0.003). On exponentiation, the estimate of the odds ratio is 6.8, with 95% confidence limits of 2.1 and 22.1. The interpretation of the odds ratio in this situation is that the estimated odds of being in a favourable outcome category when treated with the analgesic compared with placebo is 6.8, whether favourable is defined as complete relief or moderate/complete relief.
SAS code and output
PROC GLIMMIX; CLASS patient period treat;
MODEL outc=period treat/DIST=MULT LINK=CLOGIT SOLUTION OR;
RANDOM patient;Note that, in this example, if the option DDFM = KR is used in the model statement, the denominator degrees of freedom erroneously appear as 1.
Number of Observations Read | 60 | |
Number of Observations Used | 55 | |
Response Profile | ||
Ordered | Total | |
Value | outc | Frequency |
1 | 0 | 26 |
2 | 1 | 15 |
3 | 2 | 14 |
The GLIMMIX procedure is modeling the probabilities of levels of outc having lower Ordered Values in the Response Profile table. | ||
Dimensions | ||
G-side Cov. Parameters | 1 | |
Columns in X | 6 | |
Columns in Z | 30 | |
Subjects (Blocks in V) | 1 | |
Max Obs per Subject | 55 | |
Optimization Information | ||||||||
Optimization Technique | Dual Quasi-Newton | |||||||
Parameters in Optimization | 1 | |||||||
Lower Boundaries | 1 | |||||||
Upper Boundaries | 0 | |||||||
Fixed Effects | Profiled | |||||||
Starting From | Data | |||||||
Iteration History | ||||||||
Objective | Max | |||||||
Iteration | Restarts | Subiterations | Function | Change | Gradient | |||
0 | 0 | 1 | 371.01856686 | 2.00000000 | 2.187345 | |||
1 | 0 | 0 | 386.34874615 | 0.07614525 | 1.541061 | |||
2 | 0 | 0 | 386.2767642 | 0.00860819 | 1.571373 | |||
3 | 0 | 0 | 386.30470584 | 0.00062015 | 1.571598 | |||
4 | 0 | 0 | 386.30608754 | 0.00005055 | 1.571655 | |||
5 | 0 | 0 | 386.30626243 | 0.00000363 | 1.571655 | |||
6 | 0 | 0 | 386.30627135 | 0.00000029 | 1.571655 | |||
7 | 0 | 0 | 386.30627234 | 0.00000002 | 1.571655 | |||
8 | 0 | 0 | 386.3062724 | 0.00000000 | 1.571655 | |||
Convergence criterion (PCONV=1.11022E-8) satisfied. | ||||||||
Estimated G matrix is not positive definite. | ||||||||
NOTE: The covariance matrix is the null matrix. | ||||||||
Fit Statistics | ||||||||
-2 Res Log Pseudo-Likelihood | 386.31 | |||||||
Covariance Parameter Estimates | ||||||||
Cov | Standard | |||||||
Parm | Estimate | Error | ||||||
patient | 0 | . | ||||||
Solutions for Fixed Effects | ||||||||
Standard | ||||||||
Effect | outc | period | treat | Estimate | Error | DF | t Value | Pr > |t| |
Intercept | 0 | -1.3774 | 0.5041 | 29 | -2.73 | 0.0106 | ||
Intercept | 1 | 0.09043 | 0.4577 | 29 | 0.20 | 0.8448 | ||
period | 1 | 0.4195 | 0.5359 | 22 | 0.78 | 0.4421 | ||
period | 2 | 0 | . | . | . | . | ||
treat | 0 | 1.9162 | 0.5679 | 22 | 3.37 | 0.0027 | ||
treat | 1 | 0 | . | . | . | . | ||
Odds Ratio Estimates | ||||||||
95% Confidence | ||||||||
Effect | period | treat | −period | −treat | Estimate | DF | Limits | |
period | 1 | 2 | 1.52 | 22 | 0.501 | 4.62 | ||
treat | 0 | 1 | 6.80 | 22 | 2.093 | 22.06 | ||
Type III Tests of Fixed Effects | ||||
Num | Den | |||
Effect | DF | DF | F Value | Pr > F |
period | 1 | 22 | 0.61 | 0.4421 |
treat | 1 | 22 | 11.39 | 0.0027 |
7.10 Use of results from random effects models in trial design
Once a cross-over trial has been analysed and reported, there is a subsequent question to consider. What has the present study taught us about the trial design to be used in future studies of this condition? The factors we will wish to take into consideration are the sizes of the residual and patient variance components and the dropout rates at various stages during cross-over. If between-subject variability is large compared with residual variation, a cross-over design may be vastly more efficient than a corresponding parallel group study. However, the analysis of a cross-over trial requires more assumptions than a parallel group design, and if between-subject variability is relatively small, a parallel group study may be the design of choice. If a multi-period cross-over trial experiences a substantial dropout in the later phases of the cross-over or if the required duration of each treatment is long, then an incomplete block design may be considered.
Of course, the most basic way in which we can use data from one cross-over trial to plan a succeeding trial is to use the estimate of the residual variance in standard sample size formulae (see, for example, Senn, 2002). If there has been a sequence of similar trials, then a weighted average of the estimates of the residual variance would provide a more robust figure.
The more interesting question is whether a cross-over design should be used at all. This can usually be assessed satisfactorily by comparing the standard error of the treatment differences in the cross-over trial with the standard errors that would be expected from a comparable parallel group study. We reported such information for the trial described in Section 7.5, and we now consider another example.
7.10.1 Example
We consider the results from the oral mouthwash trial, summarised in Table 7.3. The estimate of the patient variance component is 0.029 and that of the residual variance is 0.066. Thus, the estimated residual variance in a parallel group trial is 0.095, the sum of these two variance components. The expected standard error of the treatment difference in a parallel group trial with 34 patients per group (giving the comparable number of treatment periods to the cross-over trial) is

Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


