(1)
Department of Mathematics, University of Florida, Gainesville, FL, USA
9.1 Introduction
Measures for prevention and control of infectious diseases include vaccination, treatment, quarantine, isolation, and prophylaxis.
Prophylaxis is the series of measures taken to prevent a specific infectious disease. These measures can be as simple as hand-washing with soap and water, or wearing protective gear, or taking a medication to prevent a disease. Treatment is the use of an agent, procedure, or regimen, such as a drug, or bed rest in an attempt to cure or mitigate a disease. Nowadays, for most infectious diseases, medications exist that can cure or lessen the impact of the diseases, while improving the life of the patients. Diseases for which medications can offer a cure include malaria and tuberculosis. Diseases for which medications offer relief but not a cure include HIV and genital herpes.
Vaccination is the process through which killed (inactivated) or weakened microorganisms are placed into the body. Our immune system recognizes vaccine agents as foreign. That triggers an immune response, and antibodies against them are developed. As a result, if the same types of microorganisms enter the body again, they will be destroyed much faster by the antibodies. Thus, an individual that is immunized is protected against the disease. If a large majority of people are vaccinated, it is much more difficult for an outbreak of disease to occur, let alone spread. This effect is called herd immunity.
Vaccination is one of the greatest achievements of public health. Vaccination has led to the complete eradication of smallpox worldwide, and a near eradication of polio. Table 9.1 gives the reduction of disease load in the United States as a result of widespread vaccination campaigns.
Table 9.1
Achievements of vaccination in the United Statesa
Disease | Baseline years | Cases/year | Cases in 1998 | % Decrease |
Smallpox | 1900–1904 | 48,164 | 0 | 100 |
Diphtheria | 1920–1922 | 175,885 | 1 | 100 |
Pertussis | 1922–1925 | 147,271 | 6,279 | 95.7 |
Tetanus | 1922–1926 | 1,314 | 34 | 97.4 |
Poliomyelitis | 1951–1954 | 16,316 | 0 | 100 |
Measles | 1958–1962 | 503,282 | 89 | 100 |
Mumps | 1968 | 152,209 | 606 | 99.6 |
Rubella | 1966–1968 | 47,745 | 345 | 99.3 |
Hib | 1985 | 20,000 | 54+71 | 99.7 |
Vaccines do not guarantee complete protection from a disease. There remains the possibility that a vaccinated person may get the disease. Even if the host develops antibodies, some pathogens can mutate (the common cold and influenza viruses are highly efficient at this), and in any case, the immune system might still not be able to defeat the infection. The degree to which vaccinated individuals are protected against the disease is called efficacy of the vaccine.
Quarantine and isolation are two measures by which exposed or infectious individuals are removed from the population to prevent further spread of the infection. Quarantine is applied to seemingly healthy but potentially infected individuals, while isolation is applied to already infectious individuals. Isolation has been used and is being used to control many dangerous diseases. Quarantine is applied less often. It is one of the first response methods that can be used in an extreme emergency. Quarantine was implemented during the SARS epidemic of 2002–2003.
The reproduction number, computed for mathematical models involving control strategies, depends on the control strategies, and it is often called a controlled reproduction number.
9.2 Modeling Vaccination: Single-Strain Diseases
There are two points in which vaccination models can differ from one another. The first is that some models assume that vaccination is equivalent to going through the disease and treats vaccinated individuals as recovered individuals. Thus an SIR model can include vaccinated individuals without an additional class. Other models assume that vaccinated individuals have to be separated into a vaccinated class V. The second point of distinction is that some classes of models assume that individuals enter the system at a point of their life when they either get vaccinated or skip vaccination and enter the system as susceptibles. This is more or less accurate for school children. Other models allow for continuous vaccination of individuals while in the system.
9.2.1 A Model with Vaccination at Recruitment
Assume that we have a perfect vaccine, whereby everybody who is vaccinated is completely protected. Suppose we vaccinate at recruitment into the system a fraction p of individuals. So if μ N is the recruitment term, a fraction p μ N goes directly into the recovered class, and a proportion q μ N, where 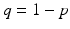 , enters the susceptible class. Thus the SIR model with vaccination becomes
, enters the susceptible class. Thus the SIR model with vaccination becomes
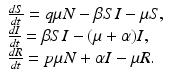
The equation of the total population size here is N′(t) = 0, and the total population size is constant, 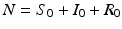 . The disease-free equilibrium, obtained from setting the derivatives equal to zero and I = 0, is given by
. The disease-free equilibrium, obtained from setting the derivatives equal to zero and I = 0, is given by 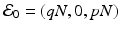 . Thus, if
. Thus, if
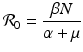 is the reproduction number in the absence of vaccination (p = 0), then
is the reproduction number in the absence of vaccination (p = 0), then 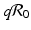 is the reproduction number of the disease in the presence of vaccination. Consequently, vaccination has reduced the original reproduction number by the fraction q.
is the reproduction number of the disease in the presence of vaccination. Consequently, vaccination has reduced the original reproduction number by the fraction q.
 , enters the susceptible class. Thus the SIR model with vaccination becomes
, enters the susceptible class. Thus the SIR model with vaccination becomes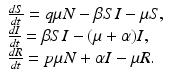
(9.1)
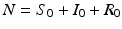 . The disease-free equilibrium, obtained from setting the derivatives equal to zero and I = 0, is given by
. The disease-free equilibrium, obtained from setting the derivatives equal to zero and I = 0, is given by 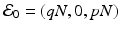 . Thus, if
. Thus, if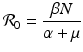
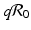 is the reproduction number of the disease in the presence of vaccination. Consequently, vaccination has reduced the original reproduction number by the fraction q.
is the reproduction number of the disease in the presence of vaccination. Consequently, vaccination has reduced the original reproduction number by the fraction q.Question: What fraction, p, of the population must be vaccinated so that the reproduction number of the disease is reduced below 1?
To answer this question, we need 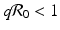 . Replacing q with 1 − p and solving the inequality for p, we obtain that
. Replacing q with 1 − p and solving the inequality for p, we obtain that 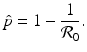
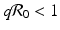 . Replacing q with 1 − p and solving the inequality for p, we obtain that
. Replacing q with 1 − p and solving the inequality for p, we obtain that 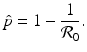
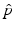 of the population is successfully vaccinated, then the disease will not spread in the population. In effect, the whole population will be protected. This is a manifestation of the herd immunity.
of the population is successfully vaccinated, then the disease will not spread in the population. In effect, the whole population will be protected. This is a manifestation of the herd immunity.9.2.2 A Model with Continuous Vaccination
Most diseases for which vaccination is successful have a recovered (immune) stage. After all, vaccination works with the immune system more or less as the disease does, so if the disease does not provide immunity, how could vaccination? However, there are diseases for which it is justified to consider vaccination in addition to an SIS model, that is, a model where recovery brings the individual back to the susceptible class. One such disease is tuberculosis, which imparts very short-lived immunity. Another situation occurs with bacterial infections with Neisseria meningitidis and Streptococcus pneumoniae. Both these bacteria can exist in the host without causing disease, a scenario, called carriage. Both carriers and infected (sick) people can transmit the microorganism, so from the point of view of disease transmission, they can be considered indistinguishable and modeled with one class. Carriage and disease impart immunity against the disease but probably not so much against carriage. Thus individuals who become completely pathogen-free can be counted as susceptible (at least for carriage). In both cases, there are vaccines, at least against some variants of the microorganisms, and an SIS model with vaccination may be appropriate.
9.2.2.1 An SIS Model with Vaccination
Let V (t) denote the number of vaccinated individuals, and ψ the per capita vaccination rate. Vaccination is applied only to healthy individuals, so only susceptible individuals get vaccinated. In this model, we also take into account the fact that vaccines are rarely perfect, and some of the vaccinated individuals can become infected and infectious even though they have been vaccinated. That happens at a reduced transmission rate β δ, where 0 ≤ δ ≤ 1 is the reduction coefficient. If δ = 0, then vaccinated individuals cannot get infected, and the vaccine is perfect. This implies that the vaccine efficacy is ε = 1. If δ = 1, then vaccinated individuals get infected just like susceptible individuals, and the vaccine plays no protective role. In that case, the vaccine efficacy is ε = 0.
We list the parameters and the variables in the Table 9.2.
Table 9.2
List of parameters, variables, and their meanings
Notation | Meaning |
Λ | Birth/recruitment rate into the population |
μ | Per capita natural death rate |
β | Per capita transmission rate |
γ | Per capita recovery rate |
χ | Proportion of individuals who recover to the vaccinated class |
1 −χ | Proportion of individuals who recover to the susceptible class |
ψ | Per capita vaccination rate |
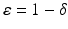 | Vaccine efficacy |
S(t) | Number of susceptible individuals |
I(t) | Number of infected individuals |
V (t) | Number of vaccinated individuals |
The model takes the form
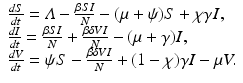
The flowchat of the model is given in Fig. 9.1.
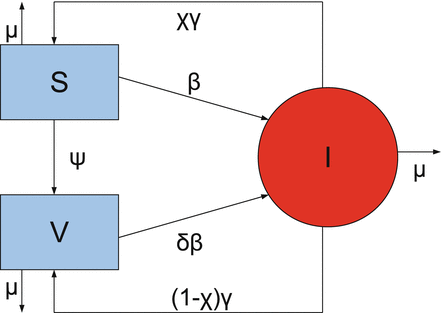
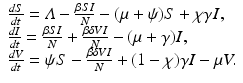
(9.2)

Fig. 9.1
Flowchart of the model with continuous vaccination with imperfect vaccine
The disease-free equilibrium is given by
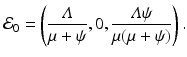 Since the equation of the total population is
Since the equation of the total population is 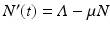 , the equilibrium total population size is
, the equilibrium total population size is 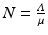 . Thus the proportions of susceptible and vaccinated in the disease-free population are given by
. Thus the proportions of susceptible and vaccinated in the disease-free population are given by

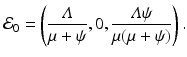
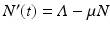 , the equilibrium total population size is
, the equilibrium total population size is 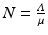 . Thus the proportions of susceptible and vaccinated in the disease-free population are given by
. Thus the proportions of susceptible and vaccinated in the disease-free population are given by
9.2.2.2 The Reproduction Number and the Critical Vaccination Proportion
To compute the reproduction number, we compute the Jacobian at the disease-free equilibrium:
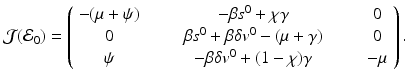
The Jacobian has two negative eigenvalues, −μ and 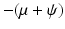 . The third eigenvalue is given by
. The third eigenvalue is given by 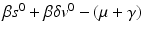 . Thus we define the reproduction number in the presence of vaccination as
. Thus we define the reproduction number in the presence of vaccination as
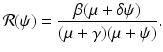 The reproduction number of the disease in the absence of vaccination is obtained by letting ψ = 0, and is given by
The reproduction number of the disease in the absence of vaccination is obtained by letting ψ = 0, and is given by
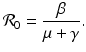
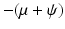 . The third eigenvalue is given by
. The third eigenvalue is given by 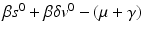 . Thus we define the reproduction number in the presence of vaccination as
. Thus we define the reproduction number in the presence of vaccination as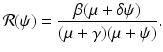
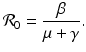
In interpreting the reproduction number, we notice that 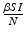 gives the number of secondary infections of susceptible individuals per unit of time. The number of secondary infections of susceptible individuals per unit of time for one infectious individual will be
gives the number of secondary infections of susceptible individuals per unit of time. The number of secondary infections of susceptible individuals per unit of time for one infectious individual will be 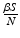 . The proportion of susceptibles in a disease-free population is
. The proportion of susceptibles in a disease-free population is 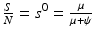 . Since
. Since 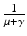 is the time spent as an infectious individual, the first term in
is the time spent as an infectious individual, the first term in 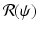 , given by
, given by 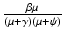 , gives the number of secondary infections of susceptible individuals that one infected individual can produce in a disease-free population. Similarly,
, gives the number of secondary infections of susceptible individuals that one infected individual can produce in a disease-free population. Similarly, 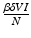 gives the number of secondary infections of vaccinated individuals per unit of time. The number of secondary infections of vaccinated individuals per unit of time for one infectious individual will be
gives the number of secondary infections of vaccinated individuals per unit of time. The number of secondary infections of vaccinated individuals per unit of time for one infectious individual will be 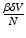 . The proportion of vaccinated individuals in a disease-free population is
. The proportion of vaccinated individuals in a disease-free population is 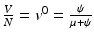 . Since
. Since 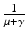 is the time spent as an infectious individual, the second term in
is the time spent as an infectious individual, the second term in 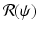 , given by
, given by 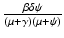 , gives the number of secondary infections of vaccinated individuals that one infected individual can produce in a disease-free population.
, gives the number of secondary infections of vaccinated individuals that one infected individual can produce in a disease-free population.
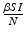 gives the number of secondary infections of susceptible individuals per unit of time. The number of secondary infections of susceptible individuals per unit of time for one infectious individual will be
gives the number of secondary infections of susceptible individuals per unit of time. The number of secondary infections of susceptible individuals per unit of time for one infectious individual will be 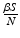 . The proportion of susceptibles in a disease-free population is
. The proportion of susceptibles in a disease-free population is 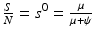 . Since
. Since 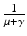 is the time spent as an infectious individual, the first term in
is the time spent as an infectious individual, the first term in 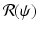 , given by
, given by 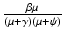 , gives the number of secondary infections of susceptible individuals that one infected individual can produce in a disease-free population. Similarly,
, gives the number of secondary infections of susceptible individuals that one infected individual can produce in a disease-free population. Similarly, 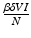 gives the number of secondary infections of vaccinated individuals per unit of time. The number of secondary infections of vaccinated individuals per unit of time for one infectious individual will be
gives the number of secondary infections of vaccinated individuals per unit of time. The number of secondary infections of vaccinated individuals per unit of time for one infectious individual will be 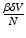 . The proportion of vaccinated individuals in a disease-free population is
. The proportion of vaccinated individuals in a disease-free population is 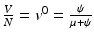 . Since
. Since 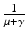 is the time spent as an infectious individual, the second term in
is the time spent as an infectious individual, the second term in 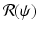 , given by
, given by 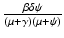 , gives the number of secondary infections of vaccinated individuals that one infected individual can produce in a disease-free population.
, gives the number of secondary infections of vaccinated individuals that one infected individual can produce in a disease-free population.One can see that the reproduction number in the presence of vaccination is a decreasing function of the vaccination rate ψ. Thus, the higher the vaccination rate, the smaller the reproduction number. Furthermore,
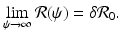 Thus, if the vaccine efficacy ε is not high enough (that is, δ is not small enough), then even if we vaccinate everybody, we may not be able to eradicate the disease. In other words, we cannot bring
Thus, if the vaccine efficacy ε is not high enough (that is, δ is not small enough), then even if we vaccinate everybody, we may not be able to eradicate the disease. In other words, we cannot bring 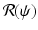 below 1, since the vaccinated individuals can become infected.
below 1, since the vaccinated individuals can become infected.
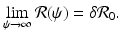
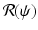 below 1, since the vaccinated individuals can become infected.
below 1, since the vaccinated individuals can become infected.Question: What is the critical proportion of individuals that should be vaccinated if the vaccine is continuously applied and imperfect?
A critical vaccination proportion 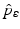 for the eradication of a disease with imperfect vaccination exists only if
for the eradication of a disease with imperfect vaccination exists only if 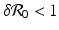 , that is, if the vaccine efficacy satisfies
, that is, if the vaccine efficacy satisfies
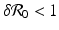 , then there exists a critical vaccination level ψ ∗ such that
, then there exists a critical vaccination level ψ ∗ such that 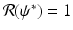 . This critical vaccination level for eradication of the disease is given by
. This critical vaccination level for eradication of the disease is given by
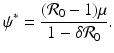 The proportion vaccinated in the population is given by
The proportion vaccinated in the population is given by 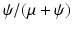 . We conclude that
. We conclude that
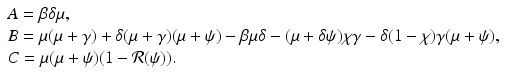
We express these coefficients as functions of 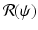 and eliminate β:
and eliminate β:

where 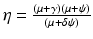 . We illustrate the backward bifurcation in Fig. 9.2.
. We illustrate the backward bifurcation in Fig. 9.2.
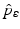 for the eradication of a disease with imperfect vaccination exists only if
for the eradication of a disease with imperfect vaccination exists only if 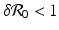 , that is, if the vaccine efficacy satisfies
, that is, if the vaccine efficacy satisfies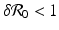 , then there exists a critical vaccination level ψ ∗ such that
, then there exists a critical vaccination level ψ ∗ such that 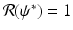 . This critical vaccination level for eradication of the disease is given by
. This critical vaccination level for eradication of the disease is given by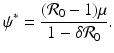
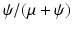 . We conclude that
. We conclude thatThe critical proportion of the population that needs to be vaccinated with vaccine with efficacy ε is given by
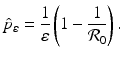 In words, the critical proportion of the population that needs to be vaccinated with imperfect vaccine is the critical population that needs to be vaccinated with perfect vaccine divided by the vaccine efficacy.
In words, the critical proportion of the population that needs to be vaccinated with imperfect vaccine is the critical population that needs to be vaccinated with perfect vaccine divided by the vaccine efficacy.
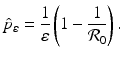
We note that the formula above is an extension of the critical vaccination proportion to imperfect vaccines. If the vaccine is perfect, that is, if ε = 1, then we obtain the customary formula for the critical vaccination proportion for perfect vaccines.
Table 9.3 gives the estimates of  before the introduction of vaccination. Most data on the reproduction number before vaccination are from England, Wales, and the USA [10]. The table gives the critical vaccination fraction with perfect vaccines, vaccine efficacies of the most common vaccines used in the USA, and the critical vaccination fractions with imperfect vaccines. It can be seen from the table that the current vaccines are incapable of eliminating pertussis, and may be useful in eliminating polio and diphtheria if a sufficient proportion of the population is vaccinated. In fact, polio has been eliminated in the developed countries for which the reproduction number before vaccination and vaccine efficacies are most accurate.
before the introduction of vaccination. Most data on the reproduction number before vaccination are from England, Wales, and the USA [10]. The table gives the critical vaccination fraction with perfect vaccines, vaccine efficacies of the most common vaccines used in the USA, and the critical vaccination fractions with imperfect vaccines. It can be seen from the table that the current vaccines are incapable of eliminating pertussis, and may be useful in eliminating polio and diphtheria if a sufficient proportion of the population is vaccinated. In fact, polio has been eliminated in the developed countries for which the reproduction number before vaccination and vaccine efficacies are most accurate.
 before the introduction of vaccination. Most data on the reproduction number before vaccination are from England, Wales, and the USA [10]. The table gives the critical vaccination fraction with perfect vaccines, vaccine efficacies of the most common vaccines used in the USA, and the critical vaccination fractions with imperfect vaccines. It can be seen from the table that the current vaccines are incapable of eliminating pertussis, and may be useful in eliminating polio and diphtheria if a sufficient proportion of the population is vaccinated. In fact, polio has been eliminated in the developed countries for which the reproduction number before vaccination and vaccine efficacies are most accurate.
before the introduction of vaccination. Most data on the reproduction number before vaccination are from England, Wales, and the USA [10]. The table gives the critical vaccination fraction with perfect vaccines, vaccine efficacies of the most common vaccines used in the USA, and the critical vaccination fractions with imperfect vaccines. It can be seen from the table that the current vaccines are incapable of eliminating pertussis, and may be useful in eliminating polio and diphtheria if a sufficient proportion of the population is vaccinated. In fact, polio has been eliminated in the developed countries for which the reproduction number before vaccination and vaccine efficacies are most accurate.Table 9.3
Diseases and their eradication vaccination levels
Disease | 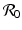 | 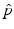 ,% ,% | Vaccine efficacya | 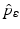 ,% ,% |
Smallpox | 3–5 | 67–80 | 0.75b | 89–100 |
Measles | 12–13 | 92 | 0.75–0.95 | 97–100 |
Mumps | 4–7 | 75–86 | 0.75–0.95 | 79–100 |
Rubella | 6–7 | 83–86 | 0.75–0.95 | 87–100 |
Chickenpox | 9–10 | 89–90 | 0.8–0.95 | 94–100 |
Pertussis | 13–17 | 92–94 | 0.8–0.9 | – |
Poliomyelitis | 6 | 83 | 0.9–0.99 | 84–92 |
Diphtheria | 4–6 | 75–83 | 0.87–0.96 | 78–95 |
9.2.2.3 Backward Bifurcation in the Imperfect Vaccination Model
The critical threshold above gives only the proportion that has to be vaccinated so that the reproduction number in the presence of vaccination is below one. However, imperfect vaccines have the disadvantage that they lead to backward bifurcation, and endemic equilibria exist and are stable even when the reproduction number in the presence of vaccination is below one. The main reason for the backward bifurcation is the fact that imperfect vaccination creates two classes of susceptible individuals with different susceptibilities—the naive susceptible and the vaccinated susceptible.
To obtain a necessary and sufficient condition for backward bifurcation, we compute the endemic equilibria. First, we consider the equations for the proportions ( ,
, 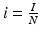 ,
, 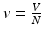 ):
):
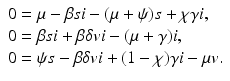
Expressing s from the first equation and v from the third equation yields
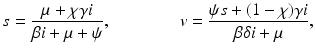 and substituting them in the second equation, we obtain a quadratic equation in i:
and substituting them in the second equation, we obtain a quadratic equation in i:
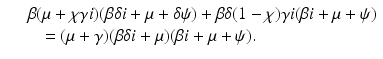
If we think of β as a function of i, that is, β(i), and we differentiate implicitly the above equation, we obtain for β′ at the critical value i = 0 the following expression:
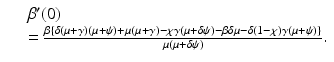 The bifurcation at the critical value i = 0 (
The bifurcation at the critical value i = 0 (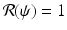 ) is backward if and only if β′(0) < 0, that is, if and only if the parameters satisfy the following condition:
) is backward if and only if β′(0) < 0, that is, if and only if the parameters satisfy the following condition:
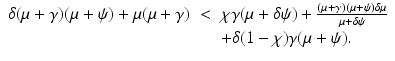 To plot the dependence of i on
To plot the dependence of i on 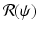 , we rewrite the equation for i as a quadratic equation in i,
, we rewrite the equation for i as a quadratic equation in i, 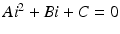 , where after dividing by β in (9.5), the coefficients are
, where after dividing by β in (9.5), the coefficients are
 ,
, 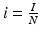 ,
, 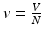 ):
):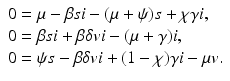
(9.4)
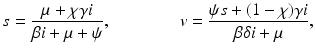
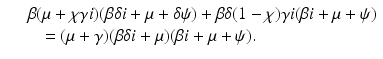
(9.5)
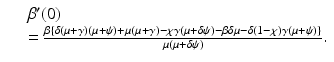
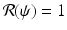 ) is backward if and only if β′(0) < 0, that is, if and only if the parameters satisfy the following condition:
) is backward if and only if β′(0) < 0, that is, if and only if the parameters satisfy the following condition: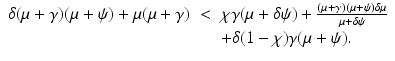
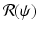 , we rewrite the equation for i as a quadratic equation in i,
, we rewrite the equation for i as a quadratic equation in i, 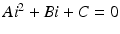 , where after dividing by β in (9.5), the coefficients are
, where after dividing by β in (9.5), the coefficients are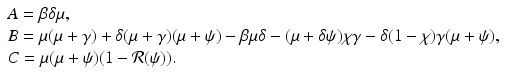
(9.6)
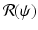 and eliminate β:
and eliminate β:
(9.7)
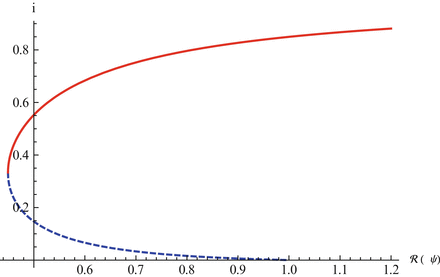
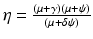 . We illustrate the backward bifurcation in Fig. 9.2.
. We illustrate the backward bifurcation in Fig. 9.2.
Fig. 9.2
The graph shows that the equilibrium value of i exhibits backward bifurcation as a function of the vaccine-dependent reproduction number. The parameters are taken as follows: μ = 0. 01, γ = 3, χ = 1, δ = 0. 1, ψ = 1
Imperfect vaccines lead to backward bifurcation. It is not hard to see that in the model above, backward bifurcation does not occur if the vaccine is perfect, δ = 0. Also, if there is no vaccination ψ = 0, then backward bifurcation does not occur. In this case, it can be seen that if 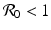 , the disease-free equilibrium is globally stable.
, the disease-free equilibrium is globally stable.
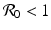 , the disease-free equilibrium is globally stable.
, the disease-free equilibrium is globally stable.The presence of backward bifurcation means that in practice, if we vaccinate with imperfect vaccine, we may need to reduce the vaccine reproduction number not below one but below a much smaller value under which there are no endemic equilibria. Thus, it may appear that vaccinating with imperfect vaccine makes the task of controlling the disease harder rather than easier. However, it must be noted that at the same time, vaccination increases the parameter space of the remaining parameters where the vaccine-dependent reproduction number is below one, and the disease-free equilibrium is locally stable. To illustrate this idea, assume that μ, ψ, and δ are given and fixed. Then in the absence of vaccination, the region in the (γ, β)-plane where the disease-free equilibrium is stable is given by μ +γ > β, since there, 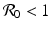 . In the presence of vaccination, the region of local stability of the disease-free equilibrium is given by
. In the presence of vaccination, the region of local stability of the disease-free equilibrium is given by
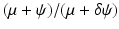 is greater than one.
is greater than one.
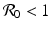 . In the presence of vaccination, the region of local stability of the disease-free equilibrium is given by
. In the presence of vaccination, the region of local stability of the disease-free equilibrium is given by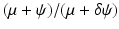 is greater than one.
is greater than one.9.3 Vaccination and Genetic Diversity of Microorganisms
When a pathogen is represented by several variants, they may not all be included in the vaccine. The strains that are included in the vaccine are called vaccine strains. The number of strains included in the vaccine is called vaccine valency. For instance, the flu vaccine is trivalent, that is, it contains three strains.
The immunity that a vaccine creates is specific to those strains that are included in the vaccine. The vaccine may provide partial immunity, or no immunity at all, to strains that are not included in the vaccine. That makes impossible the eradication of diseases whose causative agents mutate and that are represented by multiple variants.
Biologists report an increase of genetic diversity after the introduction of vaccination [142]. In terms of modeling, this says that vaccination should cause coexistence of pathogen variants, in other words, vaccination is a coexistence mechanism. To see this, we consider the model above with two strains. We assume that one of the strains is a vaccine strain with respect to which the vaccine is perfect. With respect to the other strain, the vaccine offers only partial protection. The model with two strains and vaccination becomes
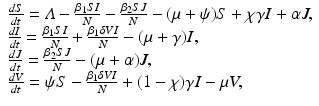
where I(t) is the number infected with the first strain, and J(t) is the number infected with the second strain. The parameter α is the per capita recovery rate from the second strain. Recovered individuals from the second strain go to the susceptible class, because only susceptible individuals can become infected with the second strain. The second strain is assumed to be the vaccine strain. The reproduction number of the first strain is as before:
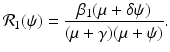 The reproduction number of the second strain is
The reproduction number of the second strain is
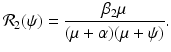
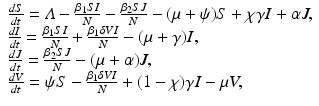
(9.8)
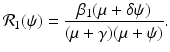
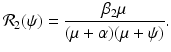
Proving the existence of a unique coexistence equilibrium is possible but not trivial. So to see the coexistence, we do a simulation. Figure 9.3 illustrates the coexistence.
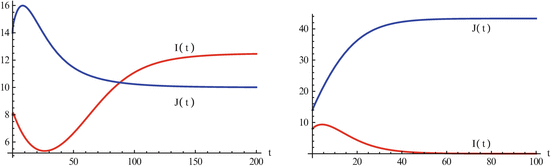

Fig. 9.3
The left figure illustrates that the number infected with strain one, I(t), and the number infected with strain two, J(t), may tend toward a coexistence equilibrium when ψ = 0. 5. The right figure illustrates that if ψ = 0, strain two eliminates strain one. The remaining parameters used for these figures are β 1 = 6, β 2 = 4. 5, γ = 0. 8, α = 0. 5, μ = 0. 1, χ = 1. 0, δ = 0. 04, Λ = 5. The corresponding reproduction numbers are given by 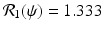 and
and 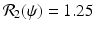 . The reproduction numbers in the absence of vaccination are
. The reproduction numbers in the absence of vaccination are 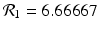 and
and 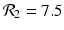
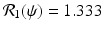 and
and 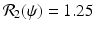 . The reproduction numbers in the absence of vaccination are
. The reproduction numbers in the absence of vaccination are 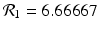 and
and 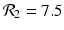
Question: What causes the coexistence? We can answer this question by examining the parts for the model that cause the coexistence. In particular, we examine the equations for the coexistence equilibrium:
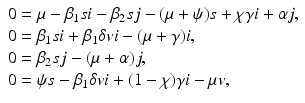
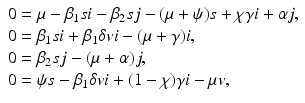
(9.9)
where as before, s, i, j, v denote the proportions. If δ = 0, then from the second and third equations, we have
 Clearly these two expressions for s are equal in very special cases, but not in general. So coexistence does not occur. Thus a necessary condition for coexistence is the imperfection of the vaccine. If there is no vaccination, that is, ψ = 0 and χ = 1 (no recovery to the vaccinated class), then v = 0, and s must satisfy the same two expressions. So coexistence does not occur. Thus vaccination, and particularly vaccine imperfections, are the cause of coexistence.
Clearly these two expressions for s are equal in very special cases, but not in general. So coexistence does not occur. Thus a necessary condition for coexistence is the imperfection of the vaccine. If there is no vaccination, that is, ψ = 0 and χ = 1 (no recovery to the vaccinated class), then v = 0, and s must satisfy the same two expressions. So coexistence does not occur. Thus vaccination, and particularly vaccine imperfections, are the cause of coexistence.

When a disease is caused by a pathogen of multiple variants, not all of them are included in a vaccine (for various reasons). Vaccination is carried out under several scenarios:
1.
Vaccination is carried against the dominant subtype. For instance, Haemophilus influenzae is represented by six serotypes: a, b, c, d, e, f, but before vaccination was instituted, serotype b caused most disease. Vaccination is now carried out against serotype b.
2.
Vaccination is carried out against several strains that account for most cases. For instance, Streptococcus pneumoniae is represented by more than 90 serotypes, but only 23 of the most common ones are included in the polysaccharide vaccine.
3.
When possible, vaccination is carried out against all subtypes (possibly one by one). For instance, poliomyelitis (caused by poliovirus, PV) is represented by three serotypes. Vaccination against each one is necessary, but polio has been nearly eradicated.
When vaccination is carried out against only one or more but not all of the pathogen variants, what is observed is decline in the number of disease cases caused by those variants included in the vaccine. At the same time, disease cases caused by other pathogen variants not included in the vaccine rise. This phenomenon is called strain (serotype) replacement (Table 9.4). The main mechanism by which serotype replacement occurs is that the vaccine has differential effectiveness: it is very effective with respect to some strains, and very little effective, or not effective at all, with respect to other strains. Thus vaccinated individuals are removed from the susceptible pool of the vaccine strains but effectively added to the susceptible pool of the nonvaccine strains, since the vaccine strains can no longer infect them.
Disease | Vaccine | Increase in | Region |
H. influenzae | Hib | Nontype b | Alaska |
Hib
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

|