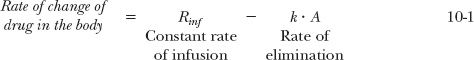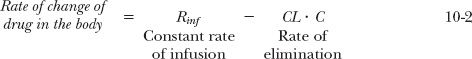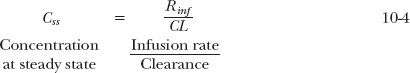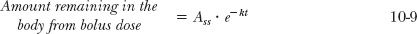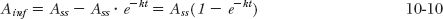Constant-Rate Input

OBJECTIVES

The reader will be able to:

• Define steady-state (or plateau) plasma concentration and describe the factors controlling it.
  
• Describe the relationship between half-life of a drug and time required to approach steady state following a constant-rate input with or without a bolus dose.
  
• Estimate the values of half-life, volume of distribution, and clearance of a drug from plasma concentration data obtained during and following constant-rate intravenous (i.v.) input.
  
• Determine the bolus dose needed to achieve the same amount in the body, or same plasma concentration, as that achieved at steady state on infusing the drug at a given rate.
  
• Determine the input rate needed to maintain the bolus amount in the body, or the initial plasma concentration, with time after giving an i.v. bolus dose.
  
• Use pharmacokinetic parameters to predict the plasma concentration and the amount in the body with time during and following constant-rate input with or without a bolus dose.
  
• Briefly discuss why short-term infusions are generally used when a single i.v. dose is called for.
  
• Predict changes in the concentration–time course of a drug during and after a constant-rate infusion when there is an alteration in a physiologic variable that may influence the pharmacokinetics of a drug.
  
• Briefly discuss how either the pharmacokinetics or pharmacodynamics of a drug can affect the onset of drug effect during a constant-rate i.v. infusion or the continuance of effect after stopping an infusion.

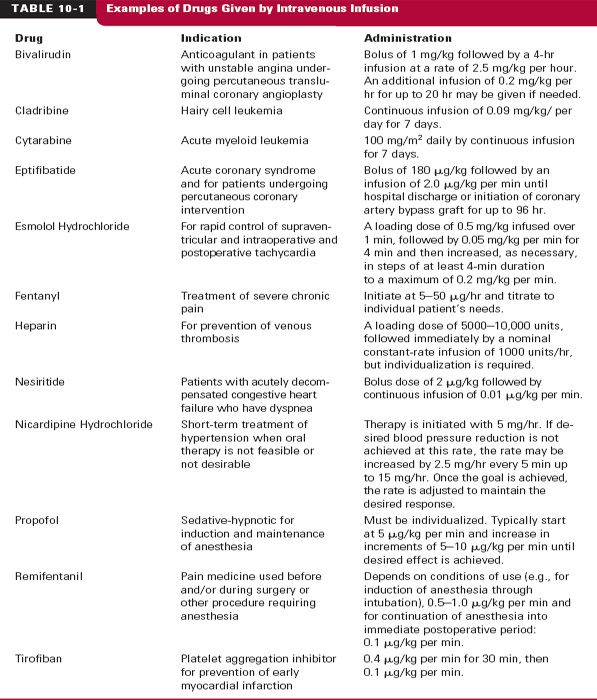
single dose may rapidly produce a desired therapeutic concentration, but this mode of administration is unsuitable when careful maintenance of plasma or tissue concentrations and effect is desired. To maintain a constant plasma concentration, drug must be administered at a constant rate. This is most often accomplished by infusing drug intravenously. No other mode of administration provides such precise and readily controlled systemic drug input. One major advantage of this method of administration is that drug input can be stopped instantly if adverse effects occur. In contrast to extravascular administration, for which drug input continues, the drug concentration immediately begins to decrease when an i.v. infusion is stopped. A disadvantage of this form of administration is that it is usually restricted to institutional settings. Examples of drugs routinely given by i.v. infusion are listed in Table 10-1. Some, like sedative–hypnotics and analgesics, which are used in anesthesia, are given by this route. Others are occasionally administered in this manner in specific situations (e.g., heparin and some barbiturates).

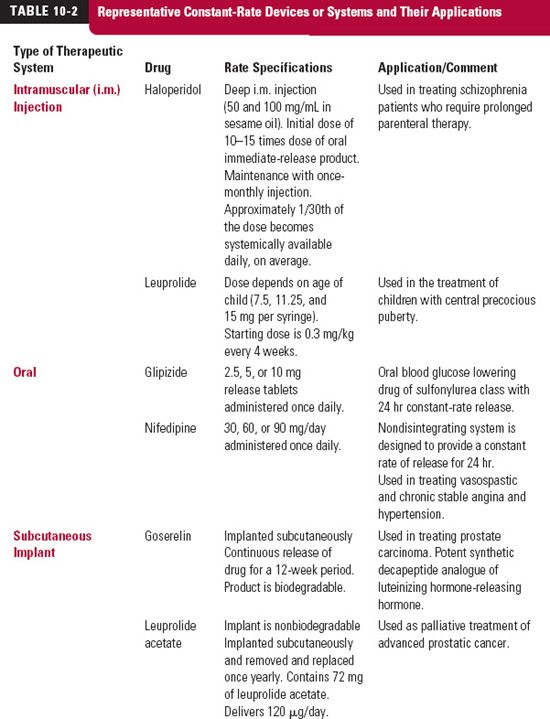
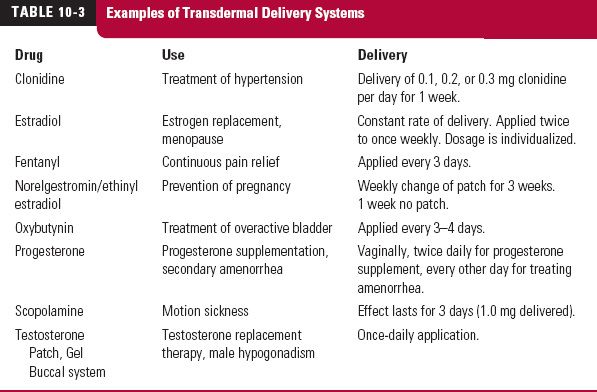
A wider application of constant-rate therapy has become possible with the development and use of constant-rate release devices and systems, which can be ingested or placed at various body sites and which deliver drug for a period extending from hours to years. Some examples of these devices/systems and their applications are given in Table 10-2. Many of the transdermal systems previously presented (Table 10-3) fall into this category as well. When used to produce a systemic effect, absorption is a prerequisite to attain effective plasma concentrations for all methods that are extravascular in nature. For the purpose of understanding the principles in this chapter, drug delivery from these systems is assumed to be equivalent to a constant-rate i.v. infusion.

This chapter also examines the turnover of the system on which a drug acts. The system affected may be any one of several constituents formed within the body. The subject is included here because the kinetic principles involved in the constant-rate input of drug are the same as those involved in the turnover of body constituents.

EXPOSURE–TIME RELATIONSHIPS

The salient features of the events following a constant-rate infusion are shown in Fig. 10-1 for tissue-type plasminogen activator (t-PA), a substance used to treat myocardial infarctions. The plasma concentration rises toward a constant value and drops off immediately after the infusion of 1.4 mg/min is stopped at 80 min. The half-life of the compound in this patient is 5.2 min, so the drug is infused for about 15 half-lives.

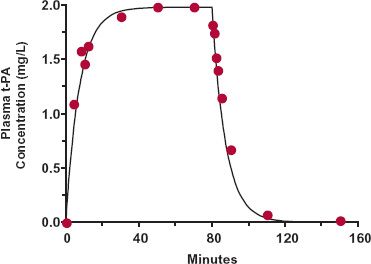
FIGURE 10-1. The plasma concentration of recombinant tissue-type plasminogen activator (t-PA) rapidly approaches a limiting value in a patient who receives 1.4 mg/min by constant-rate infusion for 80 min. At the end of the infusion, the plasma t-PA concentration drops rapidly toward zero with a 5.2-min half-life. The line is the function C = 1.98 · (1 − e^−0.133t) during the infusion, and C = 1.98 · e^−0.133t is the function postinfusion; 0.133 min⁻¹ corresponds to a half-life of 5.2 min. (From: Koster RW, Cohen AF, Kluft C, et al. The pharmacokinetics of double-chain t-PA [duteplase]: effects of bolus injection, infusions, and administration by weight in patients with myocardial infarction. Clin Pharmacol Ther 1991;50:267–277.)

A drug is said to be given as a constant (rate) infusion when the intent is to achieve and maintain a stable plasma concentration or amount in the body. In contrast to the input of a bolus dose by a short-term infusion, the duration of a constant-rate infusion is usually much longer than the half-life of the drug. The essential features following a constant infusion can be appreciated by considering the events depicted in Fig. 10-2 in which drug is introduced at a constant rate into the reservoir model previously presented (see Fig. 3-3).

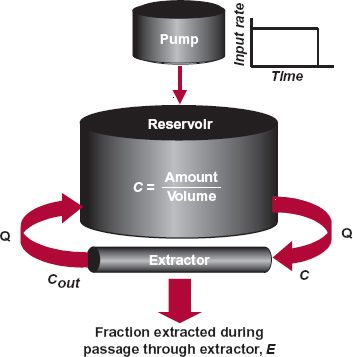
FIGURE 10-2. Drug is delivered at a constant rate (pump and rate of input shown) into a well-stirred reservoir (see Fig. 3-3). Fluid from the reservoir perfuses the extractor at flow rate Q. A fraction, E, of that presented to the extractor is removed on passing through it; the remainder is returned to the reservoir. For modeling purposes, the volume of drug solution introduced by the pump and the amount of drug in the extractor are negligible compared with the volume of the reservoir and the amount of drug contained in it, respectively.

THE PLATEAU VALUE

At any time during an infusion, the rate of change in the amount of drug in the body (or reservoir) is the difference between the rates of drug infusion and elimination. Using the model shown in Fig. 10-3, or expressing the equation in terms of the concentration of drug in plasma,

FIGURE 10-3. The time course of the amount of drug in the body during a constant-rate infusion depends on the rate of input and the rate of elimination. The simplest model for examining the time course is shown. The symbols are: R_inf, rate of infusion; A, amount in the body; V, volume of distribution; and k, the elimination rate constant. The rate of elimination is equal to k · A; the plasma concentration is equal to A/V.

On starting a constant infusion, the amount in the body (reservoir) is zero, and hence, there is no elimination; therefore, amount in the body rises. The rise continues until the rate of elimination matches the rate of infusion. Amount in the body (reservoir) and plasma concentration are then said to have reached a steady state or plateau, which continues as long as the same infusion rate is maintained. Because the rate of change of amount in the body (reservoir) at plateau is zero, it follows that Eqs. 10-1 and 10-2 simplify to:

Clearly, the only factors governing amount at plateau are the rate of infusion and the elimination rate constant. Similarly, only infusion rate and clearance control the steady-state plasma concentration. For example, consider the case of eptifibatide (Integrilin), a reversible inhibitor of platelet aggregation, used to treat acute coronary syndrome. Furthermore, suppose, for illustrative purposes, that a steady-state plasma eptifibatide concentration of 1 mg/L is desired in a 70-kg patient. Because the clearance of this drug is 4 L/hr (57 mL/hr per kilogram), the required infusion rate is 4.0 mg/hr. As the elimination rate constant of eptifibatide is 0.28 hr⁻¹, the corresponding amount of drug in the body (reservoir) at steady state is 14.3 mg. Alternatively, the amount can be calculated by multiplying the plateau concentration (1 mg/L) by the volume of distribution of eptifibatide (14.3 L).

To emphasize the factors that control the plateau, consider the following statement: “All drugs infused at the same rate and having the same clearance reach the same plateau concentration.” This statement is true. The liver and kidneys clear only what is presented to them; the rate of elimination depends only on clearance and plasma concentration. At plateau, rate of elimination is equal to rate of infusion. The plasma concentration must therefore be the same for all drugs with the same clearance if administered at the same rate. However, amount in the body varies with volume of distribution. Only for drugs with the same clearance and volume of distribution are both plasma concentration and amount in the body at plateau the same when infused at the same rate. Now consider the next statement: “When infused at the same rate, the amount of drug in the body at steady state is the same for all drugs with the same half-life.” This statement is also true, as seen from Eq 10-3. Drugs with the same half-life have the same elimination rate constant. The elimination rate constant is the fractional rate of drug elimination, that is, the rate of elimination divided by the amount of drug in the body. At plateau, rate of elimination equals rate of infusion. Hence, amount in the body at plateau must be the same for all drugs with the same half-life when administered at the same rate. Although the amount in the body is the same, the corresponding plateau concentration varies inversely with the drug’s volume of distribution.

During therapy with a drug, it is not uncommon to adjust administration to observed clinical effects. This may require an increase or decrease in dosing rate. Knowledge of the plateau value at one particular infusion rate allows prediction of the infusion rate needed to achieve other plateau values. Thus, provided that clearance is constant, a change in infusion rate produces a proportional change in plateau concentration. Returning to the eptifibatide example, one expects that a rate of 8 mg/hr is needed to produce a plateau concentration of 2 mg/L, because an infusion rate of 4 mg/hr results in a plateau concentration of 1 mg/L.

MEAN RESIDENCE TIME

Conceptually, a useful parameter to describe the sojourn of drug in the body is mean residence time (MRT). To appreciate its relationship to other pharmacokinetic parameters, consider the infusion situation. For a given constant rate of infusion, the amount of drug in the body at steady state (rate of elimination = rate of infusion) depends on the time an average molecule resides in the body. For example, if 2 × 10²⁰ molecules are eliminated per hour and they reside in the body for 10 hr, then only one tenth of the molecules in the body are removed per hour. Therefore, there must be 20 × 10²⁰ molecules in the body. Thus, MRT is related to the infusion rate and the amount in the body by the relationship:

From Eq. 10-3, it is evident that

or, as k = 0.693/t_1/2,

Furthermore, as k = CL/V, it follows from Eq. 10-6 that

For eptifibatide (V = 14.3 L, CL = 4 L/hr in the patient example), the MRT is 3.58 hr, a value corresponding (Eq. 10-7) to a half-life of 2.5 hr. The MRT concept is further discussed in Appendix H, Mean Residence Time.

TIME TO REACH PLATEAU

A delay always exists between the start of an infusion and the establishment of plateau. The sole factor controlling the approach to plateau is the half-life of the drug. To appreciate this point, consider a situation in which a bolus dose is given at the start of a constant infusion to immediately attain the amount achieved at plateau; clearly, the size of the bolus dose must be A_ss. Thereafter, the amount in the body is maintained at the plateau value by constant infusion. Imagine that a way exists to monitor separately drug remaining in the body from the bolus and that accumulating resulting from the infusion. The events are depicted in Fig. 10-4. Drug in the body associated with each mode of administration is eliminated as though the other were not present. The amount associated with the bolus dose declines exponentially and at any time,

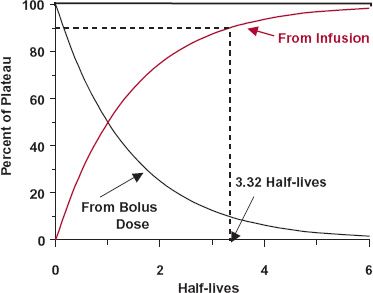
FIGURE 10-4. The approach to plateau is controlled only by the half-life of the drug. Depicted is a situation in which a bolus dose immediately attains and a constant infusion thereafter maintains a constant amount in the body (solid horizontal line). As the amount of the bolus dose remaining in the body (black line) falls, there must be a complementary rise resulting from the infusion (colored line). By 3.32 half-lives, the amount in the body associated with the infusion has reached 90% of the plateau value.

However, as long as the infusion is maintained, this decline is exactly matched by the gain resulting from the infusion. This must be so because the sum always equals the amount at plateau, A_ss. Therefore, it follows that the amount in the body associated with a constant infusion (A_inf) is always the difference between the amount at plateau (A_ss) and the amount remaining from the bolus dose, namely,

Or, on dividing through by the volume of distribution,

Thus, both the amount in the body and the plasma concentration (C_inf) rise asymptotically toward their respective plateau values following constant-rate drug infusion without a bolus dose.

The amount of drug in the body, or plasma concentration, expressed as a percent of the plateau value at different times after initiation of an infusion, is shown in Table 10-4. In one half-life, the value in the body is 50% of the plateau value. In two half-lives, it is 75% of the plateau value. Theoretically, a plateau is only reached when the drug has been infused for an infinite number of half-lives. Practically, however, the plateau may be considered to be reached in 3.3 half-lives (90% of the plateau). Thus, the shorter the half-life, the sooner the plateau is reached. For example, t-PA (half-life of 5 min) reaches a plateau within minutes (3.3 half-lives is 17 min), whereas it takes more than 8 hr of constant eptifibatide administration (half-life of 2.5 hr) before the plateau is reached (3.3 half-lives is 8.25 hr). The important point to remember is that the approach to plateau depends solely on the half-life of the drug. This is so whether 8 mg/hr of eptifibatide is infused to attain a plateau concentration of 2 mg/L, or the infusion rate is 4 mg/hr to attain a plateau concentration of 1 mg/L. In the former case, the eptifibatide plasma concentration at 1 half-life is one half the corresponding plateau value of 2 mg/L, or 1 mg/L. So, if one wants to achieve a plateau concentration of 2 mg/L more quickly, one can first infuse at a rate of 16 mg/hr for one half-life (2.5 hr) and then maintain the resulting 2 mg/L by halving the infusion rate to 8 mg/hr.

POSTINFUSION

After stopping an infusion, the amount or concentration in the body falls by one half each half-life. Given only the declining values of a drug, one cannot clearly determine whether a bolus or an infusion had been given. In the example of eptifibatide, 28.6 mg (2 mg/L × 14.3 L) are in the body (reservoir) at plateau following an infusion rate of 8 mg/hr. At 8.25 hr (3.3 half-lives) after stopping the infusion, only one tenth of the plateau value, or 2.86 mg, remains in the body. The same amount of drug would be found in the body 8.25 hr after an i.v. bolus dose of 28.6 mg.

A comment should be made about removing constant-rate devices or systems. After removing some transdermal devices, drug continues to be released from binding sites in skin for appreciable periods of time. In these instances, the plasma drug concentration falls more slowly than after stopping an i.v. infusion because of continued input of drug from the skin.

CHANGING INFUSION RATES

The rate of infusion of a drug is sometimes changed during therapy because of excessive toxicity or an inadequate therapeutic response. If the object of the change is to produce a new plateau, then the time to go from one plateau to another, whether higher or lower, depends solely on the half-life of the drug.

Consider, for illustrative purposes, a patient stabilized on a 4-mg/hr infusion rate of eptifibatide, which, with a clearance of 4 L/hr, should produce a plateau concentration of 1.0 mg/L. Suppose that the situation now demands a plateau concentration of 2.0 mg/L. This new plateau value is achieved by doubling the infusion rate to 8 mg/hr. Imagine that, instead of increasing the infusion rate, the additional 4 mg/hr is administered at a different site and that a way exists to monitor drug in the body from the two infusions separately. The events illustrated in Fig. 10-5 show that the eptifibatide concentration associated with the supplementary infusion is expected to rise to 1 mg/L in exactly the same time as in the first infusion; the concentration (1.5 mg/L) halfway toward the new plateau (2.0 mg/L) is achieved in one elimination half-life (2.5 hr) and so on. This expectation can be visualized by adding, at this time, the plasma concentration resulting from the continued initial infusion (1.0 mg/L) to the concentration arising from the supplementary infusion (0.5 mg/L). Clearly, half-life is the sole determinant of the time to go from 1.0 to 2.0 mg/L, or from any initial value to a new steady-state value during constant-rate input.

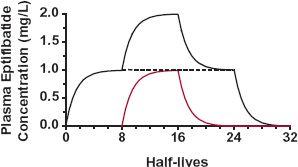
FIGURE 10-5. Situation illustrating that the time to reach a new plateau, whether higher or lower than the previous value, depends only on the half-life of a drug. A plateau concentration of 1 mg/L is reached in approximately 3.3 half-lives after starting a constant infusion of 4 mg/hr of eptifibatide. Doubling the infusion rate is like maintaining 4 mg/hr and starting another constant infusion of 4 mg/hr (colored line). In approximately 3.3 half-lives, the eptifibatide concentration rises from 1 to 2 mg/L. Halving an infusion rate of 8 mg/hr is analogous to stopping the supplementary 4-mg/hr infusion. The plasma concentration of eptifibatide returns to the previous plateau concentration of 1 mg/L in approximately 3.3 half-lives. When drug infusion is completely stopped, the concentration falls toward zero at a rate, again, depending on its half-life. The half-life of eptifibatide is about 2.5 hr. The total time span is then about 32 hr.

The decline from a high plateau to a low one is likewise related to the half-life. Consider, for example, the events after stopping the supplementary 4-mg/hr infusion rate discussed above. The eptifibatide concentration associated with this supplementary infusion falls to half of the existing value in one half-life. In 3.3 half-lives, the total concentration has almost returned to the 1.0 mg/L concentration. In addition, it will take another 3.3 half-lives for most of the eptifibatide to be removed from the body once the original 4-mg/hr infusion is also stopped.

An example of the change in plasma concentration on changing from one infusion rate to another is again demonstrated by data on t-PA in Fig. 10-6. The half-life is the determinant of the speed of attaining the new steady state. Clearance determines the steady-state concentration at any given rate of infusion.

FIGURE 10-6. The plasma concentration of plasminogen activator (t-PA) starts at about 0.6 mg/L and approaches a plateau of 0.8 mg/L following an i.v. bolus of 10 mg and a constant-rate infusion of 1.6 mg/min for 60 min to an individual subject. Subsequently, the plasma concentration drops as the drug infusion is decreased to 0.3 mg/min until 210 min when the infusion is discontinued. The time from the first steady state to the second one (0.16 mg/L) depends on the half-life of the drug, 6.6 min in this subject, as does the decline to zero after drug administration is stopped. (From: Koster RW, Cohen AF, Kluft C, et al. The pharmacokinetics of double-chain t-PA [duteplase]: effects of bolus injection, infusions, and administration by weight in patients with myocardial infarction. Clin Pharmacol Ther 1991;50:267–277.)

BOLUS PLUS INFUSION

It takes 8.25 hr of constant infusion of eptifibatide before 90% of the plateau concentration is reached in the patient with a 2.5-hr half-life. An even longer time is required for drugs with half-lives greater than that of eptifibatide. Situations sometimes demand that the plateau be reached more rapidly, as is the case for eptifibatide. One solution, as previously stated, is to double the infusion rate for the first half-life. Figure 10-2 suggests another solution. That is, at the start of an infusion, give a bolus dose equal to the amount desired in the body at plateau. Usually, the bolus dose is a therapeutic dose, and the infusion rate is adjusted to maintain the therapeutic level. When the bolus dose and infusion rate are exactly matched, as in Fig. 10-2, the amounts of drug in the body associated with the two modes of administration are complementary; the gain from the infusion offsets the loss of drug from the bolus.

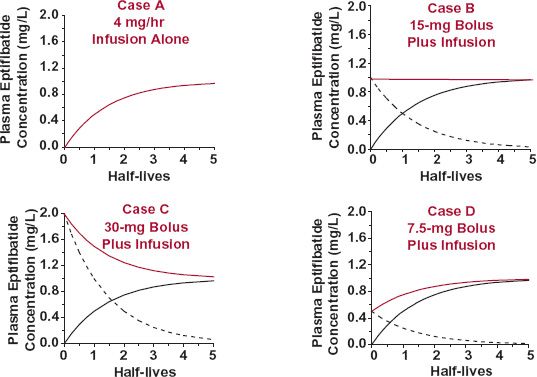
Now consider two situations. The first, shown in Fig. 10-7, is one in which different bolus doses are given at the start of a constant-rate infusion. In Case A, drug is infused at a rate of 4 mg/min and the plasma concentration rises, reaching a plateau of 1 mg/L in approximately four half-lives. In Case B, a bolus dose of 15 mg immediately attains, and the infusion rate thereafter maintains the concentration. In Case C, the bolus dose of 30 mg is excessive; because the rate of loss is initially greater than the rate of infusion; consequently, the concentration falls. This fall continues until the same plateau as in Case B is reached. It should be noticed that the time to reach the plateau depends solely on the half-life of the drug. Thus, in Case C at one half-life, the concentration of 1.5 mg/L, composed of 1 mg/L remaining from the bolus and 0.5 mg/L arising from the infusion, lies midway between the values immediately after the bolus dose and the concentration achieved by the infusion. By two half-lives, the concentration of 1.25 mg/L lies 75% of the way toward the plateau. By 3.3 half-lives, only 10% of the initial concentration resulting from the bolus remains and the concentration from the infused drug is 0.9 mg/L. We are now (1.1 mg/L) within 10% of the plateau. In Case D, the bolus dose of 7.5 mg is below the plateau amount. Because the rate of infusion now exceeds the rate of drug elimination, the plasma concentration continuously rises until the same plateau, as in the previous cases, is reached. Once again, the time to approach the plateau is controlled solely by the half-life of the drug.

FIGURE 10-7.

Stay updated, free articles. Join our Telegram channel

Join