II. Concentrations and Dilutions

A. Concentration may be expressed as a percentage. There are three types of percentages:

1. Weight-in-weight (w/w) percentage preparations
   
   a. Use weight-in-weight percentage when the final product is a solid (e.g., powder, ointment) and the component for which you are measuring the percentage is also a solid. Units in the numerator and denominator must be the same (e.g., lb./lb., gr./gr.).
   
   
   
   (1) Example: 2 g of sulfur in 100 g of a final ointment would be 2 g/100 g = 0.02 = 2% w/w
   
   
2. Volume-in-volume (v/v) percentage preparations
   
   a. Use volume-in-volume percentage when the final product is a liquid (e.g., solution) and the component for which you are measuring the percentage is also a liquid. Units in the numerator must be the same as in the denominator (e.g., mL/mL, pt./pt.).
   
   
   
   (1) Example: 5 mL of a flavoring oil in 100 mL of mouthwash would be 5 mL/100 mL = 0.05 = 5% v/v
   
   
3. Weight-in-volume (w/v) percentage preparations
   
   a. Use weight-in-volume percentage when the final product is a liquid, as indicated by the (v) in the denominator (e.g., suspensions), and the component for which you are measuring the percentage is a solid, as indicated by the (w) in the numerator. In w/v percentages, the numerator is always expressed in grams and the denominator is always expressed in milliliters. This differs from w/w and v/v percentages, where the units must be the same for both the numerator and denominator.
   
   
   
   (1) Example: 17 g of drug K in 100 mL of a final solution would be 17 g/100 mL = 0.17 or 17% w/v

B. Ratio strength preparations

1. Ratios are another way of expressing percent, or parts per 100. For example:
   
   a. A 5% w/w product is 5 parts per 100 parts, or 5:100.
   
   b. A 20% v/v solution is 20 parts per 100 parts, or 20:100 (this could mean 20 mL of drug in 100 mL of solution, or 20 L in 100 L, etc.).
   
   c. A 15% w/v solution means 15 g of drug in 100 mL of solution, or 15:100.
   
2. Ratio strength calculations are performed like percentage calculations.
   
   a. Example: 5% w/v = 5 g in 100 mL = 1 g in 20 mL = 1:20
   
3. Ratios should always be reduced so that the number “1” is written to the left of the colon (e.g., 1:100, not 2:200, even though these ratios are equal).
   
   a. Example: 3:15 could also be written: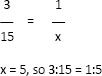
   
   

C. Stock solutions

1. Stock solutions are concentrated solutions used to make weaker strength solutions.

D. Diluting stock preparations

1. A dilution involves taking a certain percentage solution and adding a 0% diluent to decrease the percentage concentration.
   
   a. Example: How much water would you add to 100 mL of a 15% potassium chloride solution to get a 5% final product?
   
   
   
   This problem cannot be solved by simple ratio and proportion because you are looking for an inverse relationship (i.e., the more solvent we add, the lower the percentage). Instead, use this formula:
   
   (old volume)(old %) = (new volume)(new percent), which is also expressed as: (O.V.)(O.%) = (N.V.)(N.%)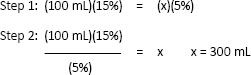
   
   
   
   Note: 300 mL is the final and total dilution you have made by adding 100 mL of 15% KCl to a certain volume of water. It is not the amount of water added.
   
   Step 3: 300 mL final solution – 100 mL of 15% = 200 mL of H₂O added

III. Alligation Methods

A. Alligation alternate method

1. Basic principles
   
   a. Use the alligation alternate method for making dilutions when the diluent is zero percent or higher. (Previous dilution examples used a zero percent diluent only.)
   
   b. This method determines how many “parts” of each diluent will be needed to get the % final product.
   
   c. “Parts” can have any value (e.g., mL, gr., pinches).
   
   d. The “parts” added together will equal the total parts of the final product.
   
   e. You can only dilute to an intermediate percent. For example, you cannot add 10% to 20% and get a percent higher than 20% or lower than 10%. The final product will be somewhere between 10% and 20%.
   
2. Examples
   
   a. If you need a 10% sulfur ointment and have only 5% and 20% ointments available, use the alligation alternate method to determine how many “parts” of each will be needed to get the 10% final product.
   
   
   
   First, find the absolute differences between the desired and the existing percentages:
   
   
   
   
   (1) Subtract 5% from 10% to get 5 parts.
   
   (2) Subtract 10% from 20% to get 10 parts.
   
   
   
   
   Next, apply the part values to the alternate percentages to set up a ratio:
   
   
   
   
   (3) The ratio is 5 parts of 20%:10 parts of 5%.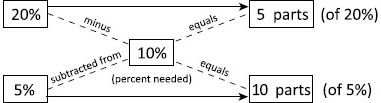
   
   
   
   
   b. Using data from the previous example, prepare 1 kg of the 10% sulfur ointment.
   
   
   
   Step 1: Add the parts, i.e., 5 + 10 = 15 parts (Note: The 15 parts represent the total quantities of the 20% and 5% ointments that are being combined. The “new” product, which is a 10% ointment, is equal to 15 parts.)
   
   Step 2: 15 parts/1000 g = 10 parts/x
   x = 667 g (of 5% ointment)
   
   Step 3: 15 parts/1000 g = 5 parts/x
   x = 333 g (of 20% ointment)
   
   Note: Step 3 can be skipped by simply subtracting 667 from 1000.
   
   Answer: To compound 1000 g of 10%, add 667 g of 5% ointment to 333 g of 20% ointment.

B. Alligation medial method

1. Use the alligation medial method to obtain the average strength of a mixture of two or more substances whose concentration and percent strength are already known. This method can also be used to check an alligation alternate problem.
   
2. Example from the mixture in A.2. above:
   
   

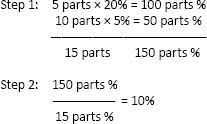
IV. Milliequivalents

A. Definitions

1. Electrolytes
   
   a. Electrolytes are important for many bodily functions that require electrical activity, such as nerve conduction and muscle contraction. Electrolyte replacement is usually ordered in units of milligrams or milliequivalents.
   
2. Milliequivalents
   
   a. A milliequivalent (mEq) is equal to the millimoles of H⁺ or OH⁻ that will react with 1 mmol of an ion or compound. When an atom has the valence of “one,” a milliequivalent (mEq) is simply equal to the atomic weight (AW) of the atom (e.g., Na⁺ = 23, so there are 23 mg/mEq).
   
   b. Example: A molecule like sodium chloride (NaCl) has a molecular weight (MW) of 58.5. Therefore, 1 mEq = 58.5 mg, and when the molecule dissociates, it yields 1 mEq Na⁺ and 1 mEq Cl⁻.

B. Converting to milliequivalents

1. Example: If a solution contains 10 g of potassium chloride (KCl), how many mEq of K⁺ does it contain? The AW of K⁺ = 39 and the AW of Cl⁻ = 35.5. Therefore, the MW of KCl = 74.5.
   
   
   
   74.5 mg = 1 mEq
   10 g = 10,000 mg
   74.5 mg/1 mEq = 10,000 mg/x = 134 mEq

C. Divalent and trivalent ions

1. Sometimes you will have an exception to the rule when you have divalent ions (e.g., Mg⁺⁺, Ca⁺⁺) and trivalent ions (e.g., Al⁺⁺⁺). In most cases when magnesium or calcium is involved in the molecule, 1 mEq is equal to 1/2 the MW. With aluminum-containing products, 1 mEq is equal to 1/3 the MW.

a. Example: Calcium chloride (CaCl₂) AW of Ca⁺⁺ = 40 AW of Cl⁻ = 35.5 40 + 35.5 + 35.5 = 111 mg total weight 1 mEq = 111/2 (i.e., valence) = 55.5 mg

V. Dry Powders for Reconstitution

A. Many unstable medications are packaged as dry powders and must be dissolved in a solvent prior to dispensing. The most frequently encountered drugs requiring reconstitution are antibiotics.

B. In most cases, reconstitutions can be accomplished in three steps:

1. Establish how much drug is in the vial or bottle.
   
2. Calculate the powder volume displacement.
   
3. Solve the problem using ratio and proportion.
   
   a. Example 1: The label on a vial reads, “Add 9.2 mL of diluent to the vial to get 10 mL of a 100 mg/mL solution for injection.” How many milliliters of the reconstituted solution would provide a 250 mg dose?
   
   
   
   
   
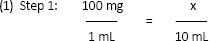
   x = 1000 mg per vial
   
   (2) Step 2: not required at this point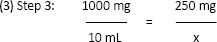
   
   
   
   x = 2.5 mL
   < div class='tao-gold-member'>
   Only gold members can continue reading. Log In or Register to continue