which is roughly the size of a cell. The domain contains blood vessels which are the sources of oxygen and nutrients. In our previous work the 2D micro-vasculature was generated using a diffusion CA model [9]. In this work we used a constrained constructive optimization (CCO) algorithm to grow the vascular network. This powerful algorithm has been used to simulate vascular network in 2D [10] and also in 3D [11]. The full description of the CCO algorithm is not provided here, but an interested reader can find more information from literature [10, 11].
In brief, the CCO algorithm grows trees in a manner that fulfils the principle of minimum blood volume, i.e., only a minimum necessary amount of blood is required to perfuse a tissue/organ. Practically an input mean flow rate and a global pressure drop need to be defined for the tree. Figure 1 shows a 3D vasculature of 2,000 vessels, with the flow rate at the root vessel being 1. 0 × 10−3 ml and the pressure drop being 5 mmHg across the tree. This vasculature will be used in the 3D domain for oxygen diffusion simulation.
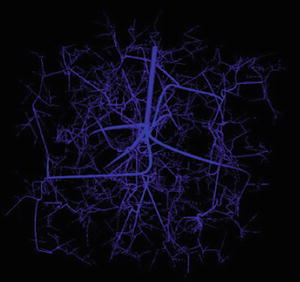
Fig. 1
Micro-vasculature generated using CCO algorithm
2.2 Oxygen Distribution
The transient diffusion equation in 3D can be expressed as [12]:
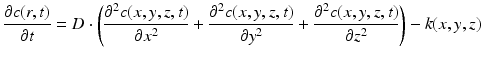
where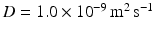 
is the diffusion coefficient [12], 
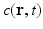is the magnitude of oxygen concentration in the whole domain at location 
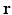and time t. With a finite difference method explicit in time (n) and centered in space (i, j, k) and without considering the oxygen consumption term k, Eq. (1) becomes:
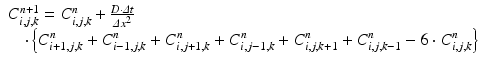
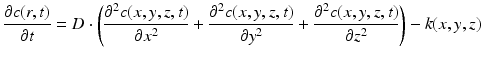
(1)
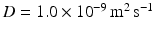is the diffusion coefficient [12], 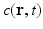is the magnitude of oxygen concentration in the whole domain at location 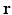and time t. With a finite difference method explicit in time (n) and centered in space (i, j, k) and without considering the oxygen consumption term k, Eq. (1) becomes: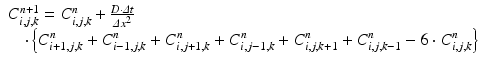(2)
As the spatial step was fixed (10 μm), step time has to be chosen to obtain a stable scheme for diffusion. Thus, stability conditions are given by the diffusion number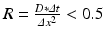 
, which gives us:
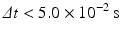and therefore Δ t = 1 ms was chosen.
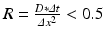, which gives us: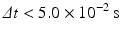A significant difference between the 2D and 3D versions of oxygen diffusion was that the computer memory for the matrix size needs to be considered, especially when floating numbers (default as the data type 64-bit double) are used for the representation of C values for the lattice. In order to reduce the computational cost, the matrix vectorization was used where the concentration at each coordinate C(i, j, k) was identified with an index l and so:
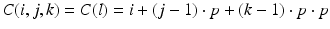
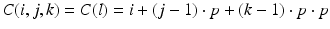
(3)
The internal computation will be made with index l but the result interpretation will be made with indexes i, j, k. A new matrix A was created which will be the basis of the computation and a standard line for A is:
![$$\displaystyle{ \begin{array}{l} A(l,:) = [C(i,j,k)C(i - 1,j,k)C(i + 1,j,k)C(i,j - 1,k) \\ \qquad \qquad C(i,j + 1,k)C(i,j,k - 1)C(i,j,k + 1)]\end{array} }$$](/wp-content/uploads/2016/10/A321864_1_En_3_Chapter_Equ4.gif)
(4)
This vectorization scheme resulted in significantly improved computation time. For example, it took around 1 h to compute the first iteration in a conventional matrix form in Matlab. With vectorization it computes much faster: about 60 s for 100 iterations, while saving all the data in a 4D-matrix (three coordinates for space and the last one for time). Without saving the data the computation time for 1,000 iterations was about 450 s.
2.3 Cellular Automata Domain and Rules
To enable cancerous/normal cells to evolve in the 3D domain, we need to define CA rules. The first rules were adapted from Alarcon et al. [1]. In brief, a cancerous cell is similar to normal cells in that it may only proliferate if oxygen is present in that element. However a cancerous cell can survive and also enter a quiescent state when no oxygen is present in that element. Once a cancerous cell enters a quiescent state, a clock is started and the cell’s functions are suspended, including proliferation. The clock is incremented at each time step if no oxygen is present in that centre element. The cell dies once the clock reaches a certain value. However, if oxygen enters the cell at any time, it returns to proliferation state and the clock is reset to zero. The CA model was run on a Neumann lattice, which in three dimensions results in six nearest neighbours (Fig. 2).
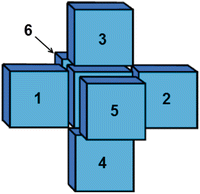
Fig. 2
Neumann neighborhood in 3D: each element has six neighbour elements
Initial proportions of normal and cancer cells in the domain were arranged as 70–30, i.e. more normal cells than cancer cells to enable the development of a normal cell colony. No difference of behaviour between cancer cells and normal cells was considered except the competition rules, which were:
1.
If a free element is surrounded by more normal cells than cancerous cells, it would become a normal cell only if there is enough oxygen for the cell to spread into the free element.
2.
If a free element is surrounded by an equal number of normal and cancer cells, it would become a cancerous cell, if there is enough oxygen for the cell to spread into the free element.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
