where S is the salt factor and F is the bioavailability or fraction of the dose administered (D) that reaches the systemic circulation.
Example 6.1 Theophylline is to be administered as its salt aminophylline (S = 0.8) in a sustained-release preparation (F = 0.9). What is the effective dose from a 400-mg tablet?
Solution
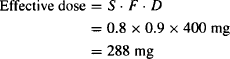
Example 6.2 A drug is administered orally as its hydrochloride salt (S = 0.95). It is susceptible to acid hydrolysis in the stomach and metabolism by CYP3A4 in the enterocytes and the liver. On average, only about 25% of a dose reaches the systemic circulation. What is the effective dose from a 5-mg tablet?
Solution
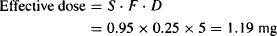
6.2.2 Rate of Drug Absorption
The process of drug absorption occurs for all routes of administration except for the direct systemic routes, such as intravenous administration. As discussed in Chapter 3, absorption is usually a first-order process. For orally administered drugs, the rate of absorption is a function of the amount of drug in the gastrointestinal tract (AGI), and the first-order rate constant for absorption (ka) and can be expressed
(6.2) 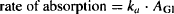
Absorption may begin as soon as the drug reaches and dissolves in the gastrointestinal fluid. The rate of drug absorption is greatest initially, when there is a lot of drug in the gastrointestinal tract. As drug is absorbed, the amount in the gastrointestinal tract decreases and the rate of absorption decreases proportionally. Eventually, the entire dose is absorbed and the absorption process ceases. At this point, drug absorption no longer has any influence on the plasma concentration–time profile. The time for absorption can be estimated as 3 to 5 absorption half–lives (where absorption t1/2 = 0.693/ka).
The key pharmacokinetic parameters for absorption are the first-order rate constant for absorption (ka), and the fraction of the dose that reaches the systemic circulation (F). Because the absorption of a drug can be influenced by the manufacturing process and the excipients contained in the dosage form, both ka and F are dependent on the specific brand of the dosage form. Thus, in contrast to other pharmacokinetic parameters, they are not necessarily constant for a drug. For example, the rate and extent of absorption of cyclosporine differ in the Noeral preparation from those in the Sandimmune preparation. These parameters (F and ka) can also be affected by anything that influences drug absorption, such as gastrointestinal motility and concomitant medications.
Other models that can be used for the rate of absorption include zero-order absorption, two parallel first-order processes, and a combination of zero- and first-order processes. If necessary, an absorption lag time can be incorporated into the absorption model.
6.2.3 Rate of Drug Elimination
As soon as drug is present in the plasma, the organs of elimination try to eliminate the drug. Elimination is a first-order process and is dependent on the plasma concentration of the drug and the amount of drug in the body. The rate is higher with higher plasma concentrations and lower with smaller plasma concentrations.
Elimination can be expressed
(6.3) 
where k is the overall elimination rate constant and Ab is the amount of drug in the body. Elimination can also be expressed using clearance:
(6.4) 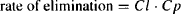
where Cl is the total body clearance.
In the equations above, clearance is the primary pharmacokinetic parameter for elimination, and the overall elimination rate constant is the secondary or dependent pharmacokinetic parameter representing the rate of elimination. The elimination rate constant is dependent on the primary parameters of clearance and volume of distribution.
6.2.4 Rate of Drug Distribution
Once in the bloodstream, a drug is able to distribute to the tissues in the body. Some tissues will take up more drug than others, and there may be certain tissues that the drug cannot access at all. As distribution proceeds, the tissue/plasma concentration ratio increases in each tissue. Eventually, a form of equilibrium is achieved, the distribution phase is complete, and the tissue/plasma concentration ratio remains constant. Thereafter the tissue concentrations and plasma concentration parallel each other. In Chapter 4 it was shown that the initial distribution of drugs is generally a first-order process and that tissue perfusion is an important determinant of the first-order rate constant for distribution. Thus, tissues take up drugs at different rates, depending on their perfusion rates. The physiological approach to pharmacokinetic modeling considers different tissues separately and uses individual tissue perfusion rates to develop models that can then be used to estimate individual tissue concentrations. A simpler approach is adopted, however, in compartmental modeling, where tissues are grouped together based on the rate at which they take up the drug. The groups of tissues constitute a compartment. Thus, a compartment is an imaginary unit that consists of a group of tissues that display similar rates of drug uptake.
There are always some tissues, usually the well-perfused tissues, where drug uptake is extremely rapid. These tissues are grouped together. There may be another group of tissues, which take up the drug with similar uptake rates but where the rate is slower than that of the well-perfused tissues. There may be a third group where uptake is exceedingly slow, perhaps because the drug partitions slowly into the tissue(s). In practice it has been found that the pharmacokinetics of almost all drugs can be described adequately using no more than three compartments; many can be described using two compartments; and when pharmacokinetics are applied to specific clinical situations (e.g., to individualize a dose for a patient), the one-compartment model can usually provide a sufficient degree of accuracy to predict the dose/plasma concentration relationship.
6.3 PUTTING EVERYTHING TOGETHER: COMPARTMENTS AND MODELS
A compartment is an imaginary unit that is used to represent a group of tissues with similar rates of drug distribution. The specific tissues that make up a compartment are unknown, and the number of compartments selected for a particular drug is based on the behavior of the plasma concentrations observed over time. A compartment is a homogeneous unit: The drug concentration is uniform throughout at all times.
As mentioned earlier, between one and three compartments are needed to produce the typical types of plasma concentration–time profiles observed clinically. One of the compartments in any model (the only one in a one-compartment model) is the central compartment, which always consists of the plasma and tissues that take up the drug rapidly. The concentration of drug in the central compartment is always equal to concentration routinely measured in vivo, the plasma concentration. One or two additional compartments may have to be added if, based on the behavior of the plasma concentrations, it appears that a significant amount of drug is distributing to some tissues at a slower rate. The organs of drug elimination are well-perfused tissues. Thus, elimination is usually, although not always, assumed to occur from the central compartment. The fundamental characteristics of each of the three compartment models are presented below.
6.3.1 One-Compartment Model
The body is viewed as a single compartment (Figure 6.1). All the tissues where a drug goes have very rapid rates of drug uptake. The distribution of the drug to the tissues is so rapid that there is no evidence of it when plasma concentrations are observed over time. When a drug is administered intravenously, even during the initial period after the injection, the plasma concentrations appear only to be influenced by drug elimination and fall monoexponentially (Figure 6.1b). There is no evidence of a distribution phase. Thus, for all intents and purposes, drug distribution can be considered to be instantaneous. The compartment is characterized by a volume, the amount of drug it contains, and the concentration of the drug. In the one-compartment model these quantities are given the symbols V1, A1, and C1, respectively. However, since the single compartment of the one-compartment model is equivalent to the central compartment, the drug concentration is equal to the plasma concentration (C1 = Cp). In the special case of a one-compartment model, A1 is equal to the amount of drug in the body (Ab). Also V1, which is A1/Cp in the one-compartment model, is the drug’s volume of distribution (Vd).
FIGURE 6.1 The one-compartment model. (a) The one-compartment model consists only of a central compartment. Distribution to those tissues that the drug can access occurs rapidly and appears to be an instantaneous process. The compartment is characterized by a volume (V1), the amount of drug it contains (A1
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


