Fig. 12.1
Overall structural of the [BChE]4-PRAD complex derived from MD simulation (Pan et al. 2009). The ribbons in color red, green, orange, and yellow represent chains a, b, c, and d of the BChE subunits, and the cyan tube represents chain e or the PRAD chain. (a) Viewed from the top of tetramerization domain of BChE. The multicolored regions refer to the active sites of the tetramer. Two of active sites in subunits indicated by chains a and c are exposed to outside solvent, while the other two face the central cavity of the BChE tetramer. (b) Viewed from the side of the twofold axis of BChE tetramer. This picture has 90° rotation from figure (a). (c) This picture has 90° clockwise rotation from figure (b) around the twofold symmetry axis
12.2.2 Doors and Dynamics of the Active Site
MD simulations have also been performed to understand how a substrate molecule can enter the active site of BChE in comparison with AChE in their monomer and tetramer structures (Fang et al. 2011). BChE and AChE are highly homologous proteins with distinct substrate preferences. The MD simulations revealed some similarities but also some differences between the AChE and BChE monomers. BChE has a larger main entrance than AChE, which seems reasonable as BChE can bind substrates as large as cocaine. Two previously proposed alternative doors (side door and back door in BChE) are larger in size than those in AChE. The acyl loop back doors in both enzymes are too small to be significant channels leading to the active sites. Based on these results, the back door and the side door are more likely and more important alternative doors than the acyl loop back door, as the former ones have larger radii and can exist for longer time. As discussed in a previous study (Tara et al. 1999a), there was no direct experimental evidence to prove the function of these alternative doors. However, multiple simulations performed by different groups using different forms of enzymes and different force fields all predicted the existence of these doors (Tai et al. 2001, 2002; Tara et al. 1999a, b; Suarez and Field 2005). Regardless, for a substrate as large as cocaine, the substrate can only enter the active site of BChE through the main door (Fang et al. 2011). In light of the MD simulations (Fang et al. 2011), the main door of BChE is significantly larger than that of AChE, which explains why BChE can have a variety of large substrates including cocaine, ghrelin, and prodrug CPT-11, whereas AChE is specific for small substrates like acetylcholine (ACh).
Further, according to the MD simulations (Fang et al. 2011), the overall structures of AChE and BChE tetramers are similar, and the gating mechanisms of the main doors of AChE and BChE are responsible for their different substrate specificities. It has also been demonstrated that both AChE and BChE tetramers could have two dysfunctional active sites due to their restricted accessibility to substrates.
12.2.3 Catalytic Mechanism for Cocaine Hydrolysis
12.2.3.1 Prechemical Reaction Process
In order to rationally design an enzyme mutant with improved catalytic activity for a given substrate, one first needs to understand the detailed catalytic mechanism including how the substrate binds with the enzyme and the subsequent chemical transformation process. Modern computational modeling and simulations can provide this detailed information. It was demonstrated that for both (−)-cocaine and (+)-cocaine, the BChE-substrate binding involves two different types of complexes: non-prereactive and prereactive BChE-substrate complexes (Zhan et al. 2003; Hamza et al. 2005). Specifically, (−)/(+)-cocaine first slides down the substrate-binding gorge to bind to W82 and stands vertically in the gorge between D70 and W82 (non-prereactive complex) and then rotates to a position in the catalytic site within a favorable distance for nucleophilic attack and hydrolysis by S198 (prereactive complex). In the prereactive complex, cocaine lies horizontally at the bottom of the gorge. The main structural difference between the BChE–(−)-cocaine and BChE–(+)-cocaine complexes exists in the relative position of the cocaine methyl ester group (Zhan et al. 2003; Hamza et al. 2005).
The MD simulations (Hamza et al. 2005) have further revealed that the (−)-cocaine rotation in the active site of wild-type BChE from the non-prereactive complex to the prereactive complex is hindered by some residues including Y332, A328, and F329 residues in the non-prereactive complex that are significantly different from those in the prereactive complex. Compared to (−)-cocaine binding with wild-type BChE, (−)-cocaine can more strongly bind with the A328W/Y332A and A328W/Y332G mutants in the prereactive complexes. More importantly, the (−)-cocaine rotation in the active site of the A328W/Y332A and A328W/Y332G mutants from the non-prereactive complex to the prereactive complex did not cause considerable changes of the positions of A332 or G332, W328, and F329 residues. These results suggest that the A328W/Y332A and A328W/Y332G mutants should be associated with lower energy barriers than wild-type BChE for the (−)-cocaine rotation from the non-prereactive complex to the prereactive complex. Further, (−)-cocaine binding with the A328W/Y332G mutant is very similar to the binding with the A328W/Y332A mutant, but the position change of F329 residue caused by the (−)-cocaine rotation was significant only in the A328W/Y332A mutant, thus suggesting that the energy barrier for (−)-cocaine rotation in the A328W/Y332G mutant should be slightly lower than that in the A328W/Y332A mutant. It has also been demonstrated that (−)-cocaine binds with the A328W/Y332A/Y419S mutant in a way that is not suitable for the catalysis (Hamza et al. 2005).
Based on the computational results, both the A328W/Y332A and A328W/Y332G mutants were expected to have catalytic activity for (−)-cocaine hydrolysis higher than that of wild-type BChE, and the catalytic activity of the A328W/Y332G mutant should be slightly higher than that of the A328W/Y332A mutant, whereas the A328W/Y332A/Y419S mutant was expected to lose the catalytic activity. The computational analysis on the A328W/Y332A mutant is consistent with the known experimental data (Sun et al. 2002a), and the computational predictions concerning the A328W/Y332G and A328W/Y332A/Y419S mutants were confirmed by the experimental kinetic analysis (Hamza et al. 2005).
Further MD and potential of mean force (PMF) simulations were performed to determine the detailed enzyme-substrate (ES) binding pathway and the corresponding free energy profiles for wild-type BChE binding with (−)/(+)-cocaine and for the A328W/Y332G mutant binding with (−)-cocaine (Huang et al. 2010, 2011). It was revealed that the non-prereactive binding pathway for (+)-cocaine binding with wild-type BChE is similar to that for (−)-cocaine binding with wild-type BChE and the A328W/Y332G mutant. For each ES binding system, the simulated PMF free energy profile revealed a local minimum on the free energy surface corresponding to the formation of an ES1-like complex (in which the substrate binds with the enzyme at the presumed peripheral anionic site around the entrance of the active-site gorge) prior to the formation of the non-prereactive ES complex during the enzyme-substrate-binding process; the ES1 complex was proposed for BChE binding with smaller substrates/reactants (Masson et al. 1997, 1999). However, further evolution from the ES1-like complex to the non-prereactive ES complex is nearly barrierless, with a free energy barrier being lower than 1.0 kcal/mol (Huang et al. 2010, 2011). So the non-prereactive ES binding process should be very fast. The rate-determining step of the entire ES binding process is the further evolution from the non-prereactive ES complex to the prereactive ES complex. The combined MD and PMF simulations also demonstrated that all of the three simulated non-prereactive complexes have similar free energy profiles for the binding processes, and the calculated binding free energies are close to each other. Further accounting for the PMF-simulated free energy change from the non-prereactive ES complex to the prereactive ES complex allowed to estimate the binding free energy for the entire ES binding process. Depicted in Fig. 12.2 are obtained PMF free energy profiles for the entire ES binding process in which the right side represents the pre-ES binding state and the local minimum on the left site refers to the final state of the ES binding (i.e., the prereactive ES complex). The PMF simulations qualitatively reproduced the relative order of the experimentally derived binding free energies, i.e., ΔG bind(wild-type BChE–(−)-cocaine) < ΔG bind(wild-type BChE–(+)-cocaine) < ΔG bind(A328W/Y332G BChE–(−)-cocaine), although the simulations systematically overestimated the magnitude of the binding affinity and systematically underestimated the differences between the ΔG bind values (Huang et al. 2010, 2011).
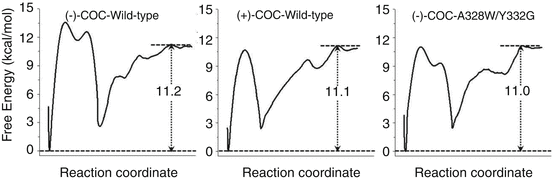

Fig. 12.2
Free energy profiles for the formation of prereactive ES complex for wild-type BChE binding with (−)-cocaine (left), wild-type BChE binding with (+)-cocaine (middle), and the A328W/Y332G mutant binding with (−)-cocaine (right)
The structural transformation from the non-prereactive ES complex to the prereactive complex was simulated through a combined use of targeted molecular dynamics (TMD) and PMF methods (Huang et al. 2010). The combined TMD and PMF simulations revealed that the structural transformation involves two transition states, denoted as TS1rot and TS2rot. The transition-state TS1rot is mainly associated with the deformation of the non-prereactive complex in which the benzoyl ester group of (−)-cocaine moves toward the catalytic residue S198 of BChE. The transition-state TS2rot is mainly associated with the formation of the prereactive complex in which the methyl ester group of (−)-cocaine rotates and the carbonyl oxygen at the benzoyl ester group of (−)-cocaine moves into the oxyanion hole of BChE. The combined TMD and PMF simulations also demonstrated that the A328W/Y332G mutations do not change the fundamental pathway for the structural transformation from the non-prereactive binding to the prereactive binding. However, the A328W/Y332G mutations significantly reduce the steric hindrance for (−)-cocaine rotation in the binding pocket of BChE and, thus, decrease the free energy barrier for the structural transformation from the non-prereactive binding to the prereactive binding. The calculated relative free energy barriers are all consistent with the experimental kinetic data (Huang et al. 2010; Hamza et al. 2005), suggesting that the computational insights are reasonable. The general computational strategy and approach (Huang et al. 2010, 2011) based on the combined TMD and PMF simulations may be also valuable in computational studies of detailed pathways and free energy profiles for other similar mechanistic problems involving ligand rotation or another type of structural transformation in the binding pocket of a protein.
12.2.3.2 Chemical Reaction Pathway
Starting from the prereactive ES complex, one may explore the detailed reaction pathway for the chemical reaction process through reaction-coordinate calculations. The first reaction-coordinate calculations on BChE-catalyzed hydrolysis of cocaine (Zhan et al. 2003) were based on the use of ab initio quantum mechanical (QM) approach and an active-site model of the enzyme. Subsequent reaction-coordinate calculations on BChE (or BChE mutant)-catalyzed hydrolysis reactions were based on hybrid quantum mechanical/molecular mechanical (QM/MM) calculations or QM/MM-free energy (QM/MM-FE) calculations (Zhan and Gao 2005; Zheng et al. 2008, 2014; Liu and Zhan 2012; Chen et al. 2011, 2012). Based on the reaction-coordinate calculations, the fundamental pathway for the chemical reaction process of BChE-catalyzed hydrolysis of (−)-cocaine (see Fig. 12.3) is essentially the same as that for BChE-catalyzed hydrolysis of other esters such as ACh, acetylthiocholine (ATC), and (+)-cocaine in terms of the covalent bond breaking and formation.
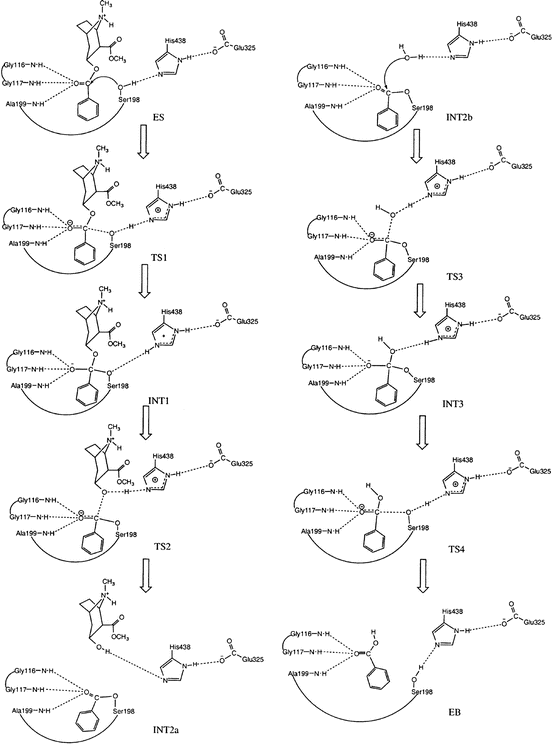

Fig. 12.3
Schematic representation of the chemical reaction pathway (Zhan et al. 2003) for BChE-catalyzed hydrolysis of (−)-cocaine at the benzoyl ester. The dash lines between the carbonyl oxygen of (−)-cocaine and backbone NH groups of residues G116, G117, and A199 refer to the potential hydrogen bonding (HB) interactions that may exist during the catalytic reaction process. However, these desirable HB interactions do not always exist for (−)-cocaine hydrolysis catalyzed by wild-type BChE
As seen in Fig. 12.3 (Zhan et al. 2003), the chemical reaction process includes both the acylation and deacylation stages. The acylation is initialized by the hydroxyl oxygen (Oγ) of S198 side chain attacking at the carbonyl carbon of the cocaine benzoyl ester to form the first tetrahedral intermediate (INT1) through the first transition state (TS1). During the formation of INT1, the C–O bond between the carbonyl carbon and S198 Oγ gradually forms, while the proton at S198 Oγ gradually transfers to the imidazole N atom of H438 side chain which acts as a general base. The second step of the acylation is the decomposition of INT1 to the metabolite ecgonine methyl ester and acyl-BChE (INT2a) through the second transition state (TS2). During the change from INT1 to INT2a, the proton gradually transfers to the benzoyl ester oxygen, while the C–O bond between the carbonyl carbon and the ester oxygen gradually breaks. Also, during the first step of acylation, the carbonyl oxygen may potentially form up to three hydrogen bonds with the NH groups of G116, G117, and A199. Note that these potential hydrogen bonds do not necessarily exist in the prereactive complex (ES) and in other structures, even though they are, for convenience, indicated throughout the reaction process in Fig. 12.3 (Zhan et al. 2003). The potential hydrogen bonds of the carbonyl oxygen of the substrate with the NH groups of G116, G117, and A199 are expected to play a key role in stabilizing the transition states during the reaction process.
It should be noted in Fig. 12.3 that there is no proton transfer between H438 and E325 throughout the reaction process. So the role of E325 is to stabilize the positively charged H438 during the reaction process, according to the aforementioned QM/MM-FE calculations at high levels. This reaction pathway is remarkably different from the double-proton transfer mechanism known for other serine hydrolases with a similar catalytic triad (Ser-His-Glu or Ser-His-Asp).
12.3 Transition-State Modeling and Simulation for Computational Enzyme Redesign
It has been well known that computational design of high-activity mutants of an enzyme is extremely challenging, particularly when the chemical reaction process is rate determining for the enzymatic reaction (Gao and Zhan 2005, 2006; Gao et al. 2006; Zheng et al. 2014). Generally speaking, for computational design of a mutant enzyme with an improved catalytic activity for a given substrate, one needs to design possible amino-acid mutations that can accelerate the rate-determining step of the catalytic reaction process (Zhan et al. 2003; Hamza et al. 2005; Zhan and Gao 2005), while other steps of the reaction are not slowed down by the mutations. It has been known (Zhan et al. 2003; Zhan and Gao 2005; Hamza et al. 2005; Gao and Zhan 2006; Pan et al. 2005) that the rate-determining step of (−)-cocaine hydrolysis catalyzed by the A328W/Y332A and A328W/Y332G mutants of BChE is the first step of the chemical reaction process. Therefore, starting from the A328W/Y332A or A328W/Y332G mutant, rational design of BChE mutants against (−)-cocaine should focus on decreasing the energy barrier for the first reaction step without significantly affecting other steps of the reaction. Thus, to computationally design a mutant with a significantly improved catalytic activity, one needs to model the possible transition-state structures associated with a variety of possible mutants of the enzyme. When a mutant of the enzyme is predicted to have a more stable transition state for the rate-determining step and, thus, is expected to have a significantly lower free energy barrier for the enzymatic reaction, the mutant will be recommended for wet experimental tests for their actual catalytic activity against (−)-cocaine (Pan et al. 2005).
12.3.1 QM/MM and QM/MM-FE Calculations
In principle, a reliable QM/MM approach may be used to evaluate the transition-state structures associated with a variety of possible mutants and predict the corresponding free energy barriers. Generally speaking, a QM/MM approach allows us to describe reaction center of an enzymatic reaction system (including the substrate atoms and key atoms in the active site of the enzyme) quantum mechanically (QM) while dealing with the remaining part of enzyme molecular mechanically (MM) and appropriately accounting for the interactions between the QM-treated atoms and the MM-treated atoms (QM/MM interactions). Different QM/MM methods differ mainly in the treatment of the QM/MM boundary atoms. A pseudobond first-principles QM/MM method has actually been used to successfully design high-activity mutants of human BChE (Zheng et al. 2008, 2014).
The pseudobond QM/MM method was initially implemented in revised Gaussian and Tinker programs (Zhang et al. 2000; Zhang 2005, 2006). The revised Gaussian and Tinker programs can be used to carry out the QM and MM parts of the QM/MM calculation iteratively until the full self-consistency is achieved. The pseudobond QM/MM method uses a seven-valence-electron atom with an effective core potential constructed to replace the boundary atom of the environment part and to form a pseudobond with the boundary atom of the active part. The main idea of the pseudobond approach is as follows: one considers that a large molecule is partitioned into two parts, an active part and an environment part, by cutting a covalent σ-bond Y–X. Y and X refer to boundary atoms of the environment part and the active part, respectively. Instead of using a hydrogen atom to cap the free valence of X atom as in the conventional link-atom approach, a pseudobond Yps–X is formed by replacing the Y atom with a one-free-valence boundary Y atom (Yps). The Yps atom is parametrized to make the Yps–X pseudobond mimic the original Y–X bond with similar bond length and strength and also to have similar effects on the rest of the active part. In the pseudobond approach, the Yps atom and all atoms in the active part form a well-defined QM subsystem which can be treated by a QM method. Excluding Y atom, the remaining atoms in the environment part form the MM subsystem treated by an MM method. The pseudobond ab initio QM/MM approach has been demonstrated to be powerful in studies of enzymatic reactions.
The Kentucky team developed a revised version (Zheng et al. 2008; Liu and Zhan 2012) of the Gaussian and Amber programs that allow users to use the more popularly used Amber force field in the QM/MM calculations. Compared to the original version of the revised Gaussian and Tinker programs (Zhang et al. 2000; Zhang 2005, 2006), the development of the revised version of the Gaussian and Amber programs enabled to perform parallel computing for the pseudobond QM/MM method for the first time (Zheng et al. 2008).
Using the QM/MM method, one may perform reaction-coordinate calculations to uncover a detail reaction pathway (the minimum-energy path), including the structures of all transition states, and the corresponding free energy barriers. To more accurately determine the free energy barriers for an enzymatic reaction, the QM/MM calculations can be followed by an appropriately planned free energy perturbation (FEP) calculations – the QM/MM-FE approach. In general, FEP calculations can be performed to evaluate free energy change caused by a small structural change (Kollman 1993; Beveridge and DiCapua 1989; Acevedo and Jorgensen 2010). Specifically, after the minimum-energy path is determined by the QM/MM calculations, the free energy changes associated with the QM/MM interactions can be determined by using the FEP method (Zhang et al. 2000). In the FEP calculations, sampling of the MM subsystem is carried out with the QM subsystem frozen at each state along the reaction path. The point charges on the frozen QM atoms used in the FEP calculations are determined by fitting the electrostatic potential (ESP) in the QM part of the QM/MM single-point calculations. The FEP calculations enable us to more reasonably determine the relative free energy changes due to the QM/MM interactions. Technically, the final (relative) free energy determined by the QM/MM-FE calculations is the QM part of the QM/MM energy (excluding the Coulombic interaction energy between the point charges of the MM atoms and the ESP charges of the QM atoms) plus the relative free energy change determined by the FEP calculations.
The QM/MM-FE calculations on the entire enzymatic reaction system allow the evaluation of the free energy barriers for each forward and reverse reaction step. The first-principles QM/MM-FE approach has been proven reliable in predicting the free energy barriers for enzymatic reactions (Hu and Zhang 2006; Zhang et al. 2002; Zheng et al. 2008, 2014; Liu et al. 2009a, b, 2011; Chen et al. 2011; Liu and Zhan 2012).
12.3.2 Transition-State Modeling and Simulation Using Classical Force Field
As noted above, the QM/MM-FE calculations have been proven reliable in predicting the free energy barriers for enzymatic reactions. On the other hand, the calculations using a truly reliable QM/MM approach (in which the QM calculation is performed at a high level of first-principles theory) are very time-consuming and, hence, are not suitable for virtual screening of a large number of possible mutants. It is highly desired to have a more efficient computational strategy which allows rapid modeling and simulation of the transition states associated with a variety of mutants.
For practical computational enzyme redesign, the Kentucky team developed a strategy to efficiently model and simulate the transition-state modeling using a classical force field (molecular mechanics) (Pan et al. 2005, 2007; Gao et al. 2006; Zheng et al. 2008, 2010, 2014; Yang et al. 2009; Xue et al. 2011). It should be pointed out that, in theory, computational modeling, such as energy minimization or MD simulation, using a classical force field can only simulate a stable structure corresponding to a local minimum on the potential energy surface, whereas a transition state during a reaction process is always associated with a first-order saddle point on the potential energy surface. Hence, energy minimization (or MD simulation) using a classical force field cannot directly simulate a transition state without any restraint on the geometry of the transition state. Nevertheless, if we can technically remove the freedom of imaginary vibration in the transition-state structure, then the number of the degrees of vibrational freedom (normal vibration modes) for a nonlinear molecule will decrease from 3N-6 to 3N-5 or less represents the number of atoms of the reaction system. The transition-state structure is associated with a local minimum on the potential energy surface within a subspace of the reduced degrees of vibrational freedom, although it is associated with a first-order saddle point on the potential energy surface with all of the 3 N – 6 degrees of vibrational freedom. Theoretically, the degree of vibrational freedom associated with the imaginary vibrational frequency in the transition-state structure can be removed by appropriately freezing the reaction coordinate. The reaction coordinate corresponding to the imaginary vibration of the transition state is generally characterized by a combination of some key geometric parameters (Pan et al. 2005). These key geometric parameters are bond lengths of the transition bonds, i.e., the forming and breaking covalent bonds during this reaction step of the enzymatic reaction. Thus, we just need to maintain the lengths of the transition bonds during the modeling of a transition state. Technically, we can maintain the lengths of the transition bonds by simply fixing all atoms within the reaction center, by using some constraints on the transition bonds, or by redefining the transition bonds. It should be pointed out that the purpose of performing such type of computational modeling on a transition state is only to examine the change of the protein environment surrounding the reaction center and the interaction between the reaction center and the protein environment (Pan et al. 2005).
The computational strategy for using a classical force field to efficiently model and simulate transition states in large-scale has opened doors to develop various practically useful approaches for computational enzyme redesign as noted below.
12.3.3 Free Energy Perturbation on the Rate-Determining Transition State (FEP-TS)
On the basis of the general strategy for the transition-state modeling and simulation mentioned above, a novel computational approach (Pan et al. 2007) was developed to carry out FEP simulations on the mutation-caused changes of the rate-determining transition states and directly estimate the mutation-caused shifts of the catalytic efficiency of an enzyme for a given substrate. This type of FEP approach for transition state (TS) is denoted as FEP-TS for convenience.
Depicted in Fig. 12.4 are the free energy changes associated with two reaction systems: one is the enzymatic reaction catalyzed by a reference mutant of the enzyme (or the wild-type), denoted by Enzyme 1 or E(1); the other is the enzymatic reaction catalyzed by another mutant, denoted by Enzyme 2 or E(2). As seen in Fig. 12.4, the catalytic efficiency, i.e., k cat(i)/K M(i), for the enzymatic reaction catalyzed by enzyme E(i) is determined by the Gibbs free energy change ΔG(i) of the reaction system from E(i) plus substrate S to the corresponding rate-determining transition state TS1(i). ΔG(i) is the sum of the enzyme-substrate-binding free energy ΔG ES(i) and the activation free energy ΔG av(i):
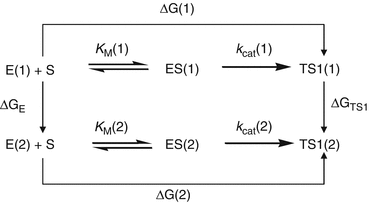
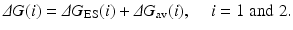

Fig. 12.4
The relationship between different free energy changes for the enzymatic reactions catalyzed by two enzymes. E(i) is the free enzyme, ES(i) represents the enzyme–substrate complex, and TS1(i) refers to the transition state (Pan et al. 2007)
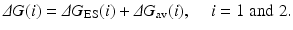
(12.1)
Assuming that a mutation on an amino-acid residue can change the enzyme from E(1) to E(2), we want to know the corresponding free energy change from ΔG(1) to ΔG(2) for the computational design of the high-activity mutants of the enzyme. There are two possible paths to determine the free energy change ΔΔG(1 → 2) ≡ ΔG(2) – ΔG(1). One path is to directly calculate ΔG ES(i) and ΔG av(i) associated with E(1) and E(2), which is very computationally demanding in terms of the level of theory. For an alternative path, the relatively less-demanding FEP simulations allow us to estimate ΔΔG(1 → 2) by determining the free energy changes ΔG E and ΔG TS1 from E(1) to E(2):
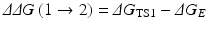
where ΔG E and ΔG TS1 are the free energy changes from E(1) to E(2) for the free enzyme and TS1, respectively. ΔG E and ΔG TS1 can be estimated by performing the FEP simulations. By using the calculated ΔΔG(1 → 2), the ratio of the catalytic efficiency associated with E(2) to that associated with E(1) can be evaluated via
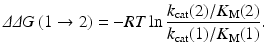
According to Eq. (12.3), one can predict the catalytic efficiency (k cat/K M) associated with E(2) from the calculated ΔΔG(1 → 2) value and the known catalytic efficiency (k cat/K M) associated with E(1) (Pan et al. 2007). Equation (12.3) can also be used to derive the experimental ΔΔG(1 → 2) value from the experimental ratio of the catalytic efficiency (k cat/K M) associated with E(2) to that associated with E(1).
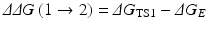
(12.2)
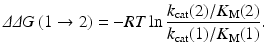
(12.3)
12.3.4 Systematic Virtual Screening of the Transition States
The basic computational strategies and methods mentioned above have been used to virtually screen a variety of hypothetical mutants of human BChE in an automated way (Pan et al. 2005, 2007; Gao et al. 2006; Zheng et al. 2008, 2010, 2014; Yang et al. 2009; Xue et al. 2011). Depicted in Fig. 12.5 is a general representation of the integrated computational–experimental effort for rational design and discovery of the enzyme mutants with an improved catalytic efficiency for a given substrate. The integrated computational–experimental effort includes the automated virtual screening of transition states, followed by wet experimental studies.
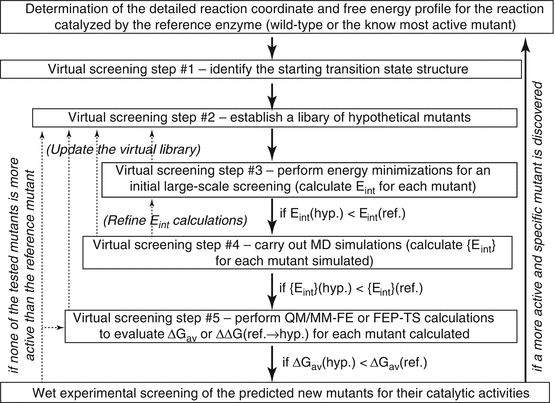

Fig. 12.5
Integrated computational-experimental effort for rational design and discovery of the enzyme mutants with an improved catalytic efficiency against a given substrate, such as (−)-cocaine. The dash lines with arrows represent the optional refinement process whenever necessary. For example, in case there is no mutant passing step #3, one may go back to step #2, updating the virtual library (with new hypothetical mutants). E int is the overall interaction energy (or another indicator for the interaction energy) between the substrate atoms and the protein environment for the hypothetical (hyp.) or the reference (ref.) mutant. {E int} (Zheng et al. 2008) refers to the dynamically averaged overall interaction energy between the substrate atoms and the protein environment for a given mutant. ΔGav is the free energy barrier for the rate-determining step of the reaction catalyzed by the hypothetical (hyp.) or reference (ref.) mutant
Using the general approach depicted in Fig. 12.5 for human BChE mutants against (−)-cocaine, the entire virtual screening process may consist of multiple steps (up to five steps depicted in Fig. 12.5). Steps #1 and #2 are for the preparation. For the preparation, step #1 is based on the detailed reaction coordinates and free energy profile determined by the QM/MM-FE calculations for the reference mutant, i.e., the most active one of the known BChE mutants against (−)-cocaine. The transition state for the rate-determining step (i.e., the step associated with the highest free energy barrier) may be used as the starting transition state for virtual screening. Starting from the rate-determining transition-state structure optimized for (−)-cocaine hydrolysis catalyzed by the reference mutant, one can conveniently build the initial structures of the transition state to be modeled for various hypothetical BChE mutants by only changing the side chains of the mutated residues.
Step #2 is to generate an appropriately designed library of hypothetical BChE mutants for practical virtual screening according to two basic requirements. The first requirement is that the library will be made sure to include BChE mutants with possibly higher catalytic efficiency against (−)-cocaine compared to the reference mutant. Certainly, this requirement can be satisfied most likely by building a complete library of all combinations of the possible mutations. Unfortunately, such a complete library would be too large to screen practically with any meaningful molecular modeling/simulation approach. Hence, the second requirement is that the library should be sufficiently small (say, < 1,000,000 or 100,000 mutants) so that the virtual screening with this library can be done practically. To satisfy both of these two necessary requirements, one must appropriately consider possible mutations on the residues that could directly or indirectly influence the reaction center based on the structural and mechanistic insights obtained from the detailed computational studies on the catalytic mechanism.
Steps #3 to #5 are for the practical computational screening at various levels. It should be noted that the ultimate criterion used in the virtual screening should be the free energy barrier (ΔGav) for the rate-determining step of the reaction process. A conceptually simple, but practically very time-consuming, way is to directly evaluate the ΔGav values associated with all of the hypothetical BChE mutants and select only a few mutants corresponding to the lowest ΔGav values for wet experimental tests. In order to speed up the virtual screening process, during the initial virtual screening steps (prior to step #5), one may first focus on the major factor affecting the free energy barrier, e.g., the interaction energy (Eint) between all atoms of (−)-cocaine and the protein environment in the rate-determining transition state, without directly calculating the free energy barrier. It has been demonstrated that the lower the interaction energy, the more stable the transition state structure (Pan et al. 2005; Zheng et al. 2008). The more stable transition-state structure means the lower energy barrier for the catalytic reaction process and, therefore, the higher catalytic efficiency. The virtual screening based on the calculation of the overall interaction energy, i.e., Eint (in step #3) or {Eint} (in step #4) shown in Fig. 12.5, without directly evaluating the ΔGav values, is computationally efficient and makes the large-scale virtual screening possible. It has also been known that a major factor affecting the overall interaction energy Eint or {Eint} for a BChE mutant is the overall hydrogen bonding (HB) interactions between the carbonyl oxygen of (−)-cocaine benzoyl ester and the oxyanion hole of the enzyme. The overall HB interactions may be represented by the total hydrogen bonding energy (tHBE). For this reason, some of the successfully accomplished virtual screening of the transition states actually evaluated tHBE, instead of Eint or {Eint} (Pan et al. 2005; Gao et al. 2006; Zheng et al. 2010, 2014).
As discussed below, the systematic virtual screening of transition states has led to successful design and discovery of human BChE mutants with considerably improved catalytic efficiency against (−)-cocaine.
12.4 Highly Efficient Cocaine Hydrolases (CocHs) Designed from Human BChE
The early rational BChE mutant design efforts were focused on the prereactive BChE–(−)-cocaine complex (ES) formation process (Sun et al. 2001, 2002a; Gao et al. 2005; Hamza et al. 2005). This strategy was reasonable because the formation of the prereactive ES complex is the rate-determining step of (−)-cocaine hydrolysis catalyzed by wild-type BChE (Zhan et al. 2003; Hamza et al. 2005; Huang et al. 2010, 2011), as noted above. Indeed, the use of this strategy led to the discovery of several mutants of human BChE with a ~9- to 34-fold improved catalytic efficiency (k cat/K M) against (−)-cocaine (Sun et al. 2002a; Hamza et al. 2005; Gao et al. 2005). In particular, cocaine rotation in the BChE active site from the non-prereactive ES complex to the prereactive ES complex is hindered mainly by the bulky side chain of Y332 residue in wild-type BChE, but the hindering can be removed by the Y332A mutation and the Y332G mutation can produce a more significant improvement (Zhan et al. 2003; Hamza et al. 2005). However, extensive computational modeling and simulations including the detailed reaction-coordinate calculations (Zhan et al. 2003; Pan et al. 2005; Zhan and Gao 2005) revealed that the rate-determining step of (−)-cocaine hydrolysis catalyzed by the A328W/Y332A mutant (Sun et al. 2002a) or A328W/Y332G mutant (Hamza et al. 2005) is the first step of the chemical reaction process. Therefore, starting from the A328W/Y332A or A328W/Y332G mutant, further efforts (Pan et al. 2005, 2007; Gao et al. 2006; Zheng et al. 2008, 2010, 2014; Xue et al. 2011) in improving the catalytic efficiency of human BChE against (−)-cocaine aimed to stabilize the transition state (TS1) for the first step of the chemical reaction process and, thus, decrease the energy barrier without significantly affecting the prechemical process and the other steps of the chemical reaction process. In these efforts, the aforementioned computational strategies and methods were used to virtually screen the transition-state structures associated with a variety of hypothetical mutants of human BChE, followed by in vitro activity assays on the actual catalytic efficiency of computationally selected mutants. The integrated computational–experimental efforts based on virtual screening of transition-state structures led to successful design and discovery of human BChE mutants (including those summarized in Table 12.1) with considerably improved catalytic efficiency against (−)-cocaine, as discussed below, without significantly changing the catalytic efficiencies against other substrates (Hou et al. 2013).
Table 12.1
Kinetic parameters determined for (−)-cocaine, (+)-cocaine, acetylcholine (ACh), acetylthiocholine (ATC), and butyrylthiocholine (BTC) hydrolyses catalyzed by wild-type human BChE and the representative mutants designed by the Kentucky team
Substrate | Enzymea | K M (μM) | k cat (min−1) | k cat/K M (min−1 M−1) | RCEb |
|---|---|---|---|---|---|
(−)-Cocaine | Wild-type BChEc | 4.5 | 4.1 | 9.1 × 105 | 1 |
A199S/A328W/Y332G | 5.1 | 560 | 1.1 × 108 | 121 | |
A199S/F227A/A328W/Y332G | 4.4 | 1,560 | 3.6 × 108 | 396 | |
A199S/S287G/A328W/Y332G | 3.1 | 3,060 | 9.9 × 108 | 1,080 | |
A199S/F227A/S287G/A328W/E441D | 1.1 | 1,730 | 1.6 × 109 | 1,730 | |
A199S/F227A/S287G/A328W/Y332G | 3.1 | 5,700 | 1.8 × 109 | 2,020 | |
(+)-Cocaine | Wild-type BChE | 4.7 | 6,420 | 1.4 × 109 | 1 |
A199S/A328W/Y332G | 5.0 | 2,820 | 5.6 × 108 | 0.40 | |
A199S/F227A/A328W/Y332G | 4.4 | 6,060 | 1.4 × 109 | 1.01 | |
A199S/S287G/A328W/Y332G | 6.3 | 5,620 | 8.9 × 108 | 0.65 | |
A199S/F227A/S287G/A328W/E441D | 4.7 | 10,800 | 2.3 × 109 | 1.68 | |
A199S/F227A/S287G/A328W/Y332G | 4.6 | 8,990 | 2.0 × 109 | 1.43 | |
ACh | Wild-type BChEd | 148 | 61,200 | 4.1 × 108 | 1 |
A199S/A328W/Y332G | 156 | 4,190 | 2.7 × 107 | 0.066 | |
A199S/F227A/A328W/Y332G | 189 | 7,430 | 3.9 × 107 | 0.095 | |
A199S/S287G/A328W/Y332G | 36 | 5,320 | 1.5 × 108 | 0.37 | |
A199S/F227A/S287G/A328W/E441D | 27 | 10,400 | 3.9 × 108 | 0.95 | |
A199S/F227A/S287G/A328W/Y332G | 37 | 11,900 | 3.2 × 108 | 0.78 | |
ATC | Wild-type BChEe | 33 | 20,200 | 6.1 × 108 | 1 |
A199S/A328W/Y332G | 31 | 3,410 | 1.1 × 108 | 0.18 | |
A199S/F227A/A328W/Y332G | 41 | 6,870 | 1.6 × 108 | 0.26 | |
A199S/S287G/A328W/Y332G | 21 | 7,880 | 3.7 × 108 | 0.60 | |
A199S/F227A/S287G/A328W/E441D | 12 | 14,000 | 1.2 × 109 | 1.99 | |
A199S/F227A/S287G/A328W/Y332G | 20 | 14,800 | 7.2 × 108 | 1.19 | |
BTC | Wild-type BChEf | 17 | 29,500 | 1.7 × 109 | 1 |
A199S/A328W/Y332G | 8.9 | 6,100 | 6.8 × 108 | 0.39 | |
A199S/F227A/A328W/Y332G | 11 | 74,700 | 6.8 × 109 | 3.91 | |
A199S/S287G/A328W/Y332G | 5.3 | 14,400 | 2.7 × 109 | 1.57 | |
A199S/F227A/S287G/A328W/E441D | 8.9 | 17,800 | 2.0 × 109 | 1.15 | |
A199S/F227A/S287G/A328W/Y332G | 13 | 28,000 | 2.2 × 109 | 1.24 |
12.4.1 First True CocH (CocH1): The A199S/S287G/A328W/Y332G Mutant
The first integrated computational–experimental effort based on virtual screening of transition-state structures, reported by the Kentucky team (Pan et al. 2005), identified that the A199S/S287G/A328W/Y332G mutant of human BChE has a significantly improved catalytic efficiency against (−)-cocaine. Based on the virtual screening of the TS1 structures, the initial in vitro activity assay was based on the measurement of the time-dependent radiometric data associated with a low concentration of [3H](−)-cocaine and fitting of the data to the kinetic equation. Such a kinetic assay was designed to quickly estimate the relative k cat/K M values of various BChE mutants without determining the individual k cat and K M values. Based on this simple assay, the A199S/S287G/A328W/Y332G mutant was estimated to have a ~456-fold improved catalytic efficiency compared to wild-type human BChE against (−)-cocaine (Pan et al. 2005). Subsequent, standard Michaelis–Menten kinetic analysis (Yang et al. 2010b) determining the individual k cat and K M values revealed that the A199S/S287G/A328W/Y332G mutant (k cat = 3,060 min−1, K M = 3.1 μM, and k cat/K M = 9.9 × 108 min−1 M−1) has ~1,080-fold improved catalytic efficiency compared to wild-type human BChE (k cat = 4.1 min−1, K M = 4.5 μM, and k cat/K M = 9.1 × 105 min−1 M−1) against (−)-cocaine without improving the catalytic efficiency against neurotransmitter ACh. Pretreatment with the mutant (i.e., 1 min prior to cocaine administration) dose dependently protected mice against the acute toxicity of a lethal dose (180 mg/kg, i.p.) of cocaine (LD100) (Xue et al. 2011). The A199S/S287G/A328W/Y332G mutant of human BChE at the dose of 0.03 mg/mouse (i.v.) (or ~0.9 mg/kg) produced full protection in mice after receiving 180 mg/kg of cocaine.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


