Fig. 25.1
NMR spectra before and after pre-treatment
In order to eliminate the effects caused by the differing magnitudes of different variables, auto-scaling (or center and scale) can be used. This is implemented as
![$$ \mathbf{z} = \left[\mathbf{x} - \mathrm{mean}\left(\mathbf{x}\right)\right]/\ \mathrm{s}\mathrm{t}\mathrm{d}\left(\mathbf{x}\right) $$](/wp-content/uploads/2016/07/A330233_1_En_25_Chapter_Equa.gif) where x is a vector of measurements for a particular variable, mean(x) is the mean of x, std(x) is the standard deviation of x, and z denotes the transformed variable. After auto scaling, the data dimension remains the same as before and all variables have the same mean and standard deviation.
where x is a vector of measurements for a particular variable, mean(x) is the mean of x, std(x) is the standard deviation of x, and z denotes the transformed variable. After auto scaling, the data dimension remains the same as before and all variables have the same mean and standard deviation.
![$$ \mathbf{z} = \left[\mathbf{x} - \mathrm{mean}\left(\mathbf{x}\right)\right]/\ \mathrm{s}\mathrm{t}\mathrm{d}\left(\mathbf{x}\right) $$](/wp-content/uploads/2016/07/A330233_1_En_25_Chapter_Equa.gif)
25.3.3 Training Set Selection
In order to build a predictive model, a training set and an independent test set are utilized. The training set is used to construct or train a model. When the model is a regression or a calibration model, it is also called a calibration set. The model is then validated using the test set. If the validation is successful, the model can then be applied to new unknown samples for prediction. Before building a proper model, it is very important to correctly split the data into a training set and a test set. The training set should be as representative of the whole data as possible. It should cover all of the spread in the population including the new unknown objects. Therefore, the measurements should always be carefully designed by the expert in order to control the span of data variance. In an article by Wu et al. (1996d), four different data splitting methods were compared. These were: D-optimal design, Kennard-Stone design, Kohonen self-organizing mapping, and random selection. It was found that the Kennard-Stone design out-performed all other methods by selecting objects that were evenly distributed in the X-space.
25.3.4 Dimension Reduction
There are three main reasons to reduce the dimensions in data analysis. The first is to reduce and eliminate the variables that are irrelevant to the study being undertaken. The second is to preserve only the variables that carry information within the data. The third is known as parsimony, which is to simplify the model with the necessary and sufficient number of variables as a model. A simple model with low number of parameters is more stable and easily interpretable than a complex model.
In general there are two ways to reduce the dimensionality of data. The first method is known as feature selection (Leardi et al. 1992; Leardi 2000; Kalivas et al. 1989; Guo et al. 2001, 2002; Wu et al. 1996a, 2003b; Baldovin et al. 1996), the process of finding the most adequate subset available of input variables for a prediction or modeling task. The second method is feature reduction (Wu et al. 1996b, 1997a, b, 2002; Wu and Manne 2000; Guo et al. 2000), such as PCA and Partial Least Squares (PLS), which extract a small number of orthogonal latent variables to replace the original variables. The latent variables are linear or non-linear combinations of the original variables and the number of orthogonal latent variables is usually lower than the number of objects.
25.3.4.1 Feature Reduction
PCA and PLS are the most popular feature reduction methods to reduce the dimensionality of the data. In PCA, the latent variables (also called factors) are linear combinations of the original variables (i.e. the weighted sum of the original variables). The number of factors is much lower than the number of original variables. The first factor is obtained in such a way as to maximize the total variance (information) in the data. The second factor is selected to be orthogonal to the first and has the maximal remaining variance, and so on. PCA is also often used as a visualization method (see Sect. 25.3.1) and can be effective when the first two factors explain most of the information i.e. variance of the data. Similar to PCA, Partial Least Squares (PLS) extracts factors by maximizing the covariance between X and Y instead of the total variance of X.
When the latent variables of principal components (PC) are used instead of the original variables to build a linear regression model, this is called Principal Component Regression (PCR). When the latent variables of PLS factors are used to build a linear regression model, this is called Partial Least Squares Regression (PLSR). After the feature reduction by PCA or PLS, the number of factors is much lower than the number of objects, and the factors are orthogonal to each other. Therefore, the two high dimensional problems of matrix singularity and collinearity are solved, and one can have enough degrees of freedom to build a regression model.
25.3.4.2 Feature Selection
In feature selection, the only possible way to be sure that “the best” set of variables are picked up is the “all-possible-models” technique, where all possible model combinations are tested. With k variables, the number of possible combinations is 2k-1; therefore this approach cannot be used due to the computational complexity unless the number of variables is low. So a compromise is used in most situations.
The simplest (but less effective) way of performing a feature selection is to operate on a “univariate” basis, by retaining those variables having the greatest correlation with the response. Here, each variable is taken into account by itself, without considering how its information “integrates” with the information brought by the other (selected or unselected) variables. As a result, if several highly correlated variables are “good”, they are all selected independent of their correlation, and the information may be highly redundant. On the other hand, those variables that are not taken into account become very important when their information is integrated with other variables. To improve the method, several multivariate methods such as the stepwise variable selection, genetic algorithms (Leardi et al. 1992; Leardi 2000) and simulated annealing (Kalivas et al. 1989) may be used.
Genetic Algorithms (GAs) are a general optimization technique that has found use in many fields (Guo et al. 2001, 2002; Wu et al. 2003b; Niazi and Leardi 2012). GAs are especially useful when the problem becomes so complex that it cannot be solved by standard techniques. In Chemometrics, GAs have been found useful in feature selection (Niazi and Leardi 2012). GAs are inspired by the theory of evolution: in a living environment, the best individuals have a greater chance of survival and a greater probability to spread their genes by reproduction. The mating of two “good” individuals causes the optimization of the offspring due to the mixing of their genomes, which may result in a “better” offspring. The terms “good”, “better”, and the “best” denote the degree of adaptation/fitness of the individuals to their environment. The application of a GA to a problem requests the implementation of five basic steps: (1) coding of variables, (2) initiation of population, (3) evaluation of the response, (4) reproduction and (5) mutation. Steps 3–5 alternate until a termination criterion is reached; the criterion can be based on a lack of improvement in the response, simply on a maximum number of generations or on the total time allowed for the process.
In the case study (see Sect. 25.4), four methods were applied for dimension reduction. The GA and Stepwise variable selection methods were applied as feature selection methods; PCA and PLS were applied as feature reduction methods to reduce the dimension of data. All these methods were integrated with an MLR method, namely GA_MLR, stepwise MLR (STP_MLR), PCR and PLSR. The results after applying these methods on data were then compared.
25.3.5 Model Optimization
There are many different modeling techniques that can be classified as linear and non-linear methods. Some classification and regression methods are discussed and their performances are compared in refs (Czekaj et al. 2005; Wu and Massart 1996, 1997; Wu et al. 1996c; Candolfi et al. 1998; Baldovin et al. 1997). In chemometrics, the most commonly used models for regression are the PCR and PLSR. In PCR and PLSR, one should optimize the number of latent variables or factors included in the model in order to reduce model complexity. Cross-validation is one of the most popular techniques to optimize the model complexity. The data are randomly divided into a given number of segments. Each segment is comprised of primary units referred to as “objects”. The cross validation method is implemented in a way that each time one segment of objects is left out and the remaining objects are used to build models with different number of factors. The responses (Y) corresponding to the left-out objects are predicted by the models. Then another segment of objects is left out and subjected to the same procedures. This is repeated until all objects have been left out once. After completion of the procedure, all objects will have been predicted once, and the entire predicted Y values are recorded. The root mean square error of cross-validation prediction (RMSECV) can be obtained (by comparing the predicted Y and observed Y values) for each model with different factors. The optimal model is denoted as the model giving the lowest RMSECV.
25.3.6 Model Evaluation and Prediction
Model over-fitting is a frequent problem and as a result the predictions may not be accurate when applied to new objects. Therefore, it is necessary to evaluate the prediction power of the model before it is applied to predict new objects. The prediction power of a model can be estimated by predicting for an independent test set of objects with known responses (Y).
When no dimension reduction is involved in the modeling, no optimization step is required as all variables are used in modeling. In such situation, cross-validation can be applied for model validation, as the predicted responses (Y) of the left-out objects are independent of the model. However, when dimension reduction is used, cross-validation is not a good validation method as all objects within the model building data set have been used in constructing the model (for optimizing for the number of factors). It is therefore no longer an independent evaluation. Therefore, an independent test set has to be acquired to validate the model.
In the case study (Sects. 25.5 and 25.6), an independent test set was used to validate the model obtained after dimension reduction.
If the prediction results of the test set are satisfactory, validation is successful. The model is fit and applied to predict the response of a new (unknown response) object. Otherwise the model has to be rejected/revised and cannot be used for prediction. In order to establish the prediction power of the optimized model, the scatter plot of the predicted response value against the observed response value of the objects in the independent test set can be looked at. If the predicted values are close to the observed values, the scatter plot will fall near the 45° line and the Pearson correlation coefficient (r) will be near 1, which indicates a model with good prediction power. When r is near 0, it indicates a poor prediction model. However, when r is in the middle such as 0.5, it is difficult to decide whether to accept or reject a model just based on r itself. A randomization test (Wu et al. 2002; Eugene 1964) can be applied in such a circumstance. The rationale of the randomization test is to examine whether the correlation coefficient obtained in the independent test set outperforms the correlation coefficient obtained in any random compositions of test sets, i.e. H0: r = 0; H1: r > 0 (Eugene 1964; Edgington 1995). This procedure can be implemented by following the steps below:
1)
Apply the model to objects in the independent test set (X test) to predict the response Y values, and calculate the correlation coefficient referred to as rorig between the predicted and observed Y values;
2)
Randomly permute each column of X test to obtain a permuted X test;
3)
Apply the model to the permuted X test to predict the responses (Y), and calculate correlation coefficient referred to as rperm between the predicted and observed Y values;
4)
Repeat steps 2–3 large enough number of times (say 1000) to obtain 1000 rperm’s;
5)
Calculate p-value (probability of prediction of random test set) by the ratio of number of rperm’s having values greater than rorig divided by 1000, or calculate the 95 % percentile of rperm’s as Upper Limit;
6)
If the p-value is less than 0.05 or rorig is higher than the Upper Limit, we can accept the model; otherwise, we reject the model.
25.4 Case Study
The example data were from a clinical phase III study (McInnes et al. 2010, 2011). There were 69 patients in the drug treatment group and 63 patients in the placebo group. The goal was to predict both the efficacy and toxicity variables after 12 weeks drug treatment using baseline variables. In the study, 66 baseline variables were measured and collected as independent variables. To eliminate the effects caused by magnitude of the measures, the auto-scale was applied to pretreat the data. In order to assess the model, the patients presented in the drug treatment group were divided into training and test sets. The training set, containing 35 subjects, was used to build and optimize a model. The test set, containing 34 subjects, was used to validate the optimal model. The other 63 subjects in the placebo group were used as a new data set to verify if the models obtained from the drug treatment group were applicable to the placebo group.
All the multivariate Chemometric methods were programmed in Matlab (MATLAB 6.1 2000).
The aim here is to build predictive models of efficacy and toxicity measures at week 12 from the baseline parameters for the drug treatment patients.
Before modelling, PCA was applied to visualize the structure of the X-data. Figure 25.2 was the score plot obtained after PCA of the patients in the DRUG TREATMENT group. It shows that the patents selected in both the training and test sets were evenly distributed and covered the whole X-space of the data. Therefore, the datasets are representative.
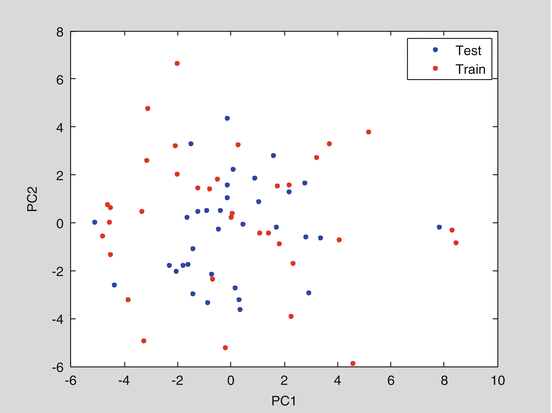

Fig. 25.2
PCA score plot of all the patients in the treatment group
25.4.1 Predictive Model for TOXICITY MEASUREMENT at Week 12
PCR, PLSR, Stepwise MLR (STW_MLR) and GA_MLR were applied to build the predictive models for TOXICITY MEASUREMENT at week 12 for the DRUG TREATMENT group. To compare the results of different methods, the Root Mean Square Error of the prediction (RMSEP) of the independent test set objects in the DRUG TREATMENT group was used. The best model should give the smallest RMSEP. In Table 25.1, the results of the prediction of the test set are listed for comparison. The results show that GA_MLR gave the smallest RMSEP (359.3) and highest correlation (r = 0.67) between the predicted and observed TOXICITY MEASUREMENT values. Therefore, GA_MLR with 10 baseline variables outperformed all the other studied methods and gave the best prediction model.
Table 25.1
Model comparison by the prediction of the test set for TOXICITY MEASUREMENT at week 12
Method < div class='tao-gold-member'>
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

|
|---|