Fig. 3.1
Intramolecular and Intermolecular forces in polymers for biomedical use
Intra and Inter Polymer Molecular Interactions
A correct understanding of many physical and chemical properties of polymeric materials is linked to the knowledge of the intra and inter molecular interactions. All matter is held together by force and its property results from the properties of individual molecules and from how they act collectively. Preeminently, it is necessary to distinguish the types of forces acting within and between molecules: including intramolecular interactions that occur between macromolecular groups itself that are responsible for the complex chemical properties and the intermolecular interactions, responsible for the physical properties. At atomic level, considering the interaction between two isolated atoms as they are brought into close proximity from an infinite separation. At large distances interactions are negligible but as the atoms approach, each exerts forces on the other. These forces are of two types attractive force (Fa) and repulsive force (Fr) and the magnitude of each is a function of interatomic distance. The origin of attractive part depends on the particular type of bonding. The repulsion between atoms is related to the Pauli principle: when the electronic clouds surrounding the atoms, they start to overlap and the energy of the system increases suddenly. The sum of attractive and repulsive components is the net force F, and then when Fa and Fr become equal there is no net force and a state of equilibrium exists. Sometimes it is more convenient to work with potential energies between two atoms instead of forces considering that energy and force for atomic systems are mathematically related:
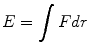
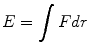
(3.1)
At equilibrium spacing r o , the force F is zero and net energy corresponds to minimum energy E 0 [14]. The binding energy require to separate two atoms from their equilibrium spacing to an infinite distance apart is the minimum energy E 0 . A large of material properties depend on E 0 , curve shape and bonding type [15].
As already said, the potential curve is the result of two terms: the contribution of attractive force at long ranges (Van der Waals force) and the repulsive term at short ranges. The curves indicate the strength of the bond based on the depth of the potential well: more deep is the well more stable is the molecule [15].
By chemical bonding is meant the effect that causes the energy of two atoms close to each other to be significantly lower than when they are apart. The effect arises from the sharing of the outer (valence) electrons of these atoms which, in the presence of two or more positively charged nuclei, rearrange themselves into spatial distributions (orbitals) where the electrons are, on the average, closer to the nuclei. The strength and length of a chemical bond are related to potential distance curve in which the minimum value of energy, the bond energy, is defined as the amount of energy required to increase the separation of the atoms forming the bond to infinity. However, what is lacking from the curves is the fact that chemical bonds, due to the redistributed electron clouds, have distinct directionality. The most widely used model for chemical bonding is the covalent bond or shared electron model. Different elements have different tendencies to draw electrons toward their nuclei. This ability is called electronegativity. Thus, in general the shared electron cloud is not evenly distributed in the space between the bonding nuclei. The difference in the electronegativities of the bonding atoms quantifies the extent how evenly or unevenly the bond electrons are shared. A purely covalent bond (i.e., completely evenly shared electrons) can only be obtained when the bonding atoms are of the same element. The atom with a smaller electronegativity, can be viewed as having a partial positive charge +δ, as the positive charge of its nuclei is not fully screened anymore by the valence electrons. The formation of one or more chemical bonds allows atoms to form energetically stable molecules which are characterized by their structure and composition. Since chemical bonds result in increased localized electron densities, it can be assumed that the spatial regions associated with different chemical bonds repel each other electrostatically. As became apparent from the discussion on chemical bonds above, many molecules contain polar chemical bonds that can be associated with electric dipoles, comprising of atomic partial charges. The molecules, in turn, as collections of these partial charges, can be associated with electric dipoles, quadrupoles, and higher multipoles. Many chemical groups in molecules may also be charged, and then the electrostatic effects are important in a wide range of molecular systems. It turns out that relating the intricate intermolecular forces to simple electrostatic interactions between charges, dipoles, and higher multipoles works surprisingly well in understanding the structure and dynamics of condensed matter systems. The long chains are held together either by secondary bonding forces such as van der Waals and hydrogen bonds or primary covalent bonding forces through cross links between chains. In general, the intermolecular interactions could be or a dipole-dipole interaction or dispersion (London) interaction. Dipole-dipole forces are referred to an electrostatic interaction acting between two permanent dipoles, averaged over different orientations due to the thermal motion of the molecules. These interactions tend to align the molecules in order to increase the attraction reducing potential energy. London dispersion interactions, instead, are of purely quantum-mechanical origin. They are caused by correlated movements of the electrons in interacting molecules. Finally, hydrogen bond occurs between molecules that have a permanent net dipole resulting from hydrogen being covalently bonded to relatively electronegative atoms (fluorine, oxygen or nitrogen). Hydrogen bonds are a stronger intermolecular force than either dispersion forces or dipole-dipole interactions. Inter and intramolecular interactions are generally present in several polymers largely used for biomedical applications, which have very long chain molecules, formed by covalent bonding along the backbone chain. In addition, each chain can have side groups, branches, and copolymeric chains or blocks which can also interfere with the long-range ordering of chains. In the case of branched polymers in which side chains are attached to the main backbone chain, chain packing is limited by the steric hindrance of side chains resulting in a not ordered structure.
Molecular Weight Polidispersivity and Effects on Polymer Viscosity
Because polymers are long-chain molecules, their properties tend to be more complex than their short-chain counterparts. Thus, in order to choose a polymer type for a particular application, microscopic properties of polymers must be understood [16]. Among them, polymer molecular weight is important because it determines many physical properties. Some examples include the transitions temperatures from liquids to rubbers, solids and mechanical properties such as stiffness, strength, viscoelasticity, toughness, and viscosity. If molecular weight is too low, the transition temperatures and the mechanical properties will generally not be adequate for the use in commercial applications in terms of transition temperatures or mechanical properties for load bearing application. Unlike small molecules, however, the molecular weight of a polymer is not one unique value. Rather, a given polymer will have a distribution of molecular weights that will depend on the way the polymer is produced. For polymers we should not speak of a molecular weight, but rather of the distribution of molecular weight or of the average molecular weight. There are many ways, however, to calculate an average molecular weight. The question therefore is how ones can define the average molecular weight for a given distribution of molecular weights.
The answer is that the type of property being studied will determine the desired type of average molecular weight. For example, strength properties may be influenced more by high molecular weight molecules than by low molecular weight molecules and thus the average molecular weight for strength properties should be weighted to emphasize the presence of high molecular weight polymer. The molecular weight of polymer is described by two statistically useful definitions: the number average and weight average molecular weights. The number average molecular weight is correlated to the number of molecules present in the mixture. This average molecular weight follows the conventional definition for the mean value of any statistical quantity. In polymer science is called the number average molecular weight (M N ) that therefore is an average over the number of molecules.
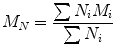
where N i is the number of moles of species, and M i is the molecular weight of speciesi. By considering the polymer property which depends on the size or weight of each polymer molecule, it is possible to define the weight average molecular weight (M W ). It represents an average over the weight of each polymer chain.
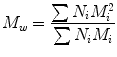
where N i is the number of moles of speciesi, and M i , is the molecular weight of speciesi [17]. In general, a series of average molecular weights can be defined by the equation:
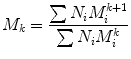
where
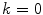
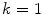
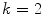
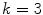
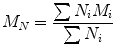
(3.2)
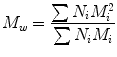
(3.3)
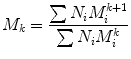
(3.4)
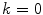
gives M N
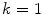
gives M W
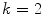
gives M z
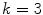
gives M z+1
One average molecular weight which does not fit into the general expression of M k is the viscosity average molecular weight, M v that is given by the Mark-Houwink and defined as:
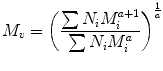
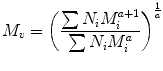
(3.5)
Here a represents a constant that depends on the polymer/solvent pair used in the viscosity experiments.
For all synthetic polydisperse polymers, the various average molecular weights always rank in the follow order:
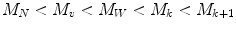
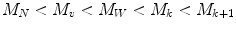
(3.6)
For monodisperse polymers all molecules have the same molecular weight, then all molecular weight averages are equal [18]. To measure an average molecular weight, it is possible to use a colligative property which yields M N or light scattering which yields M W . A molecular weight distribution for a typical polymer is shown in Fig. 3.2; it seems like a probability distribution curve.
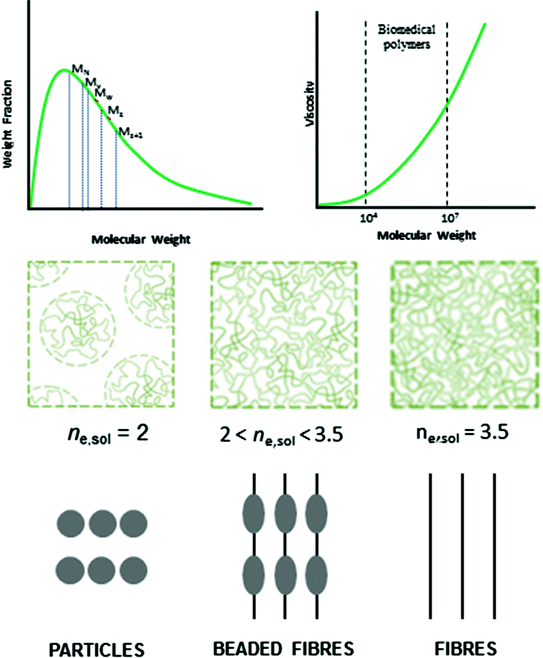

Fig. 3.2
Typical molecular weight distribution and viscosity dependence for biomedical polymers. Effect of entanglement molecular weight and viscosity on the morphology of electrospinning/spraying products
Standard deviation of molecular weight is used in order to characterize the spread of the distribution function.
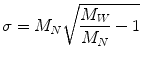
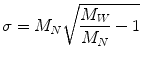
(3.7)
A key term in the standard deviation is the ratio of M W to M N . This term is known as the polydispersivity index and it is used as a measure of the breadness of the molecular weight distribution. The polydispersity index or dispersity D is commonly used to measure the distribution of molecular mass in a given polymer sample:
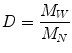
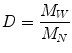
(3.8)
So, the dispersity calculated is the weight average molecular weight (M W ) divided by the number average molecular weight (M N ) indicating in this way the distribution of individual molecular masses in a batch of polymers [19].
Linear polymers used for biomedical applications generally have M N in the range of 25,000–100,000 and M N from 50,000 to 30,000. Higher or lower molecular weights may be necessary, depending on the ability of the polymer chains to exhibit secondary interactions such as hydrogen bonding which may concur to additional strength. In general, increase molecular weight corresponds to an increase of physical properties [16] such as viscosity. Equally the intrinsic viscosity can be related to the molecular weight of the solute and gives an idea of molecular weight. For solutions of polymers with M N > 10,000 Dalton, it is possible to consider the Mark-Houwink relation:
![$$\left[ \eta \right] = KM^{a}$$](/wp-content/uploads/2017/03/A320747_1_En_3_Chapter_Equ9.gif)
where K and a are constants characteristic of the particular system investigated. K is referred to the particular solvent-solute pair and “a” is particularly related to the shape of the solute molecule.
![$$\left[ \eta \right] = KM^{a}$$](/wp-content/uploads/2017/03/A320747_1_En_3_Chapter_Equ9.gif)
(3.9)
Values of these parameters have been determined for a large number of polymer-solvent pairs in the range of molecular weights normally of interest for characterization purposes [20]. For instance molecular weight of the polymer also has an important effect on morphologies of electrospun scaffold. Here, the electric field forces permit to modify the size scale of fibres from micro to nano-meter in order to obtain micro or nanostructured scaffolds. In these applications, molecular weight is correlated with the solution viscosity, then considering the same concentration of the same polymer increasing molecular weight is possible to switch from microspheres to fibres. Interestingly, during the electrospinning and electrospraying process, the morphology from beads to fibres changes as the solution viscosity: droplet shape in the case of lower viscosity until smooth fibres when the sufficient viscosity is achieved [21], as shown in Fig. 3.2. In the case of intermediate values of viscosities, Zong et al. [22] have demonstrated the formation of droplets (i.e., beads) along the fibres, also underlining the possibility to control the spacing between the beads as the viscosity changes. In particular, it has been observed that by properly choosing polymer molecular weight and concentration, it is possible to discriminate between the formation of fibres or particles. In addition, chain entanglements may strongly affect size and morphology of the obtained particles, thus offering tunable release kinetics suitable for different drug delivery systems [23, 24]. It is well-known that particle morphology obtained by electrospraying is mainly determined by the competition between chain entanglement and Coulomb fission within a single droplet. More in detail, as the solvent evaporates from the droplet, two competing factors occur: the increase of polymer concentration and, consequently, of entanglements which stabilize the droplet from further subdivision thus preserving its spherical shape—and, secondly the increase of surface charge which can overcome the surface tension thus leading to droplet fission and the formation of ‘‘offspring droplets’’. Considering that polymer chain entanglements oppose the Coulomb fission during the electrospraying process, some researchers [25] have identified a not dimensional parameter to describe the transition between fibre and bead formation and, consequently, between electrospraying and electrospinning process—as a function of the entanglements forming among chains in solution. This parameter n e,sol is defined as the ratio between polymer number average molecular weight (M n ) and M e , which is the average molecular weight of the polymer segments between two entanglements in solution. So, it is possible to distinguish three different regimes in the electrospinning/spraying process of polymer solutions: n e,sol < 2, in this case, particle formation occurs; n e,sol > 3.5, regular electrospinning with fibre formation appears. In the intermediate case, 2 < n e,sol < 3.5, a mixed regime yielding beads and fibres takes place [26] (Fig. 3.2).
Furthermore, molecular weight and viscosity are extremely important parameters for the processing of melt polymers at different temperatures. In scaffold design for tissue engineering, polymer blends have been largely investigated to obtain porous substrates with high control of pores interconnections and anisotropy. The mixing and extrusion of immiscible blends composed of polymers with different molecular weight, i.e., polycaprolactone (PCL) and poly (ethylene oxide) (PEO) is an interesting example where the sage balance of viscosity and relative composition play a crucial role on the final morphology of the scaffold. In this case, to reach a co-continuous phase organization—i.e., fully percolation of polymer phases,—it is possible to study ab initio the viscosity ratio, depending upon the relative volume fraction of components in the binary polymer blend as follows.
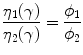
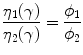
(3.10)
In agreement with basic rules of co-continuous blends, a viscosity ratio equal to 1 should lead to a phase inversion at a 50:50 composition. However, when two components have different viscosities, the less viscous component (i.e., lower molecular weight) usually tends to encapsulate the more viscous one (i.e., higher molecular weight), thus pushing the phase inversion point toward a blend that is richer in the most viscous component [27]. In the case the viscosity gap between the blend components is relatively modest, a phase inversion point close to 50/50 (% vol) may be expected. According to this idea [28], through the complex viscosity curve, it is possible to reach the isoviscosity condition that represents the essential requirement to obtain an optimal mixing of the polymer blend.
Thermal Properties: Effect of Crystalline and Amorphous Phases
Molecular shape arrangements are important factors in determining the physical properties of polymers. The molecular structure, conformation and orientation of the polymers have a relevant effect on the organization of molecules on the micro and macroscopic scale as they aggregate into more ordered structures. In order to explain this phenomena, crystalline and amorphous phase are generally recognized. In particular, polymer whose molecular structure lacks a definite repeating form, shape or structure is called amorphous polymer and has no definite shape while the polymer in which a unit structure repeats itself is called crystalline and has a definite shape, form and structure. There are some polymers that are completely amorphous, but most are a combination with the tangled and disordered regions surrounding the crystalline areas, called semicrystalline polymers. The presence of crystallites in the polymer usually leads to enhanced mechanical properties, unique thermal behavior, and increased fatigue strength. These properties make semicrystalline polymers desirable materials for biomedical applications.
As a function of the peculiar chain organization is possible to identify three important physical transitions: glass transition, melting point and crystallization. These phenomena are important with respect to the design and processing of polymeric materials and maybe controlled by thermal conditions. Crystallization is the process by which, upon cooling, an ordered solid phase is produced from liquid melt having a highly random molecular structure. The melting transformation is the reverse process that occurs when a polymer is heated and the glass transition occurs with amorphous or non crystallizable polymers. Of course, during the physical steps of crystallization, melting and glass transition it is possible to observe changes in physical and mechanical properties of polymers. In the case of semi-crystalline polymers, the non-crystalline regions undergo the phenomenon of the glass transition, while the crystalline regions are affected by the melt phenomenon. The understanding of the mechanism and dynamics of crystallization in polymers is important since the degree of crystallinity affects the thermal and mechanical properties of these materials. Crystallization from a melt is the most fundamental of all phase transformations in materials that occurs through the nucleation and growth processes. Furthermore, the crystallization is a process associated with partial alignment of polymer molecular chains. These chains fold together and form ordered regions called lamellae, which compose larger spheroidal structures named spherulites. The crystallization proceeds with the formation of isolated spherulites, which then grow until their mutual impingement with further slow crystallization. In a sample of crystalline polymer there are billions of spherulities. There is an initial induction time required for the formation of spherulitic nuclei, followed by a period of accelerated crystallization in which spherulites grow in radius. When the spherulites begin to touch each other, crystallization rates slow down again. Complete crystallinity is almost never achieved, and the final degree of crystallinity is molecular-weight-dependent. Crystallization at low temperature nucleates a great number of spherulites which grow slowly while at high temperature crystallization results in rapid growth of relatively few spherulites, influencing in this manner the morphology of polymers.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


