Key Concepts
 When research involves time-related variables, such as survival and recurrence, we generally do not know the outcome for all patients at the time the study is published, so these outcomes are called censored.
When research involves time-related variables, such as survival and recurrence, we generally do not know the outcome for all patients at the time the study is published, so these outcomes are called censored.
 Observations are doubly censored when not all patients enter the study at the same time.
Observations are doubly censored when not all patients enter the study at the same time.
 An example of why special methods are needed to analyze survival data helps illustrate the logic behind them.
An example of why special methods are needed to analyze survival data helps illustrate the logic behind them.
 Life table or actuarial methods were developed to show survival curves; although generally surpassed by Kaplan–Meier curves, they occasionally appear in the literature.
Life table or actuarial methods were developed to show survival curves; although generally surpassed by Kaplan–Meier curves, they occasionally appear in the literature.
 Survival analysis gives patients credit for how long they have been in the study, even if the outcome has not yet occurred.
Survival analysis gives patients credit for how long they have been in the study, even if the outcome has not yet occurred.
 The Kaplan–Meier procedure is the most commonly used method to illustrate survival curves.
The Kaplan–Meier procedure is the most commonly used method to illustrate survival curves.
 Estimates of survival are less precise as the time from entry into the study becomes longer, because the number of patients in the study decreases.
Estimates of survival are less precise as the time from entry into the study becomes longer, because the number of patients in the study decreases.
 Survival curves can also be used to compare survival in two or more groups.
Survival curves can also be used to compare survival in two or more groups.
 The logrank statistic is one of the most commonly used methods to learn if two curves are significantly different.
The logrank statistic is one of the most commonly used methods to learn if two curves are significantly different.
 The hazard ratio is similar to the odds ratio; the difference is that the hazard ratio compares risk over time, while the odds ratio examines risk at a given time.
The hazard ratio is similar to the odds ratio; the difference is that the hazard ratio compares risk over time, while the odds ratio examines risk at a given time.
 The Mantel–Haenszel statistic is also used to compare curves, not just survival curves.
The Mantel–Haenszel statistic is also used to compare curves, not just survival curves.
 Several versions of the logrank statistic exist. The logrank statistic assumes that the risk of the outcome is the constant over time.
Several versions of the logrank statistic exist. The logrank statistic assumes that the risk of the outcome is the constant over time.
 The Mantel—Haenszel statistic essentially combines a number of 2 × 2 tables for an overall measure of difference.
The Mantel—Haenszel statistic essentially combines a number of 2 × 2 tables for an overall measure of difference.
 The hazard function gives the probability that an outcome will occur in a given period, assuming that the outcome has not occurred during previous periods.
The hazard function gives the probability that an outcome will occur in a given period, assuming that the outcome has not occurred during previous periods.
 The intention-to-treat principle states that subjects are analyzed in the group to which they were assigned. It minimizes bias when there are treatment crossovers or dropouts.
The intention-to-treat principle states that subjects are analyzed in the group to which they were assigned. It minimizes bias when there are treatment crossovers or dropouts.
Presenting Problems
Lung cancer is the leading cause of cancer deaths in men and in women between the ages of 15 and 64 years of age. Small-cell lung cancer accounts for 20–25% of all cases of lung cancer. At the time of diagnosis, 40% of the patients with small-cell cancer have disease confined to the thorax (limited disease) and 60% have metastases outside of the thorax (extensive disease). Current standard chemotherapy for extensive disease using a combination of cisplatin and etoposide yields a median survival of 8–10 months and a 2-year survival rate of 10%. Preliminary studies using a combination of cisplatin with irinotecan resulted in a median survival of 13.2 months. For this reason, Noda and colleagues (2002) at the Japan Clinical Oncology Group conducted a prospective, randomized clinical trial to compare irinotecan plus cisplatin with etoposide plus cisplatin. The primary endpoint was overall survival. Secondary endpoints included rates of complete and overall response. A complete response was defined as the disappearance of all clinical and radiologic evidence of a tumor for at least 4 weeks.
Over a 3-year period, 154 patients with histologically confirmed small-cell cancer and extensive disease (defined as distant metastasis or contralateral hilar-node metastasis) were enrolled. All patients were evaluated weekly. Tumor response was assessed by chest radiograph and chest CT.
We use data from this study to illustrate methods for analyzing survival data. A sample of 26 patients is used to show actual calculations, but results from the entire study are also given. Data from the study are available in a data set entitled “Noda” on the CD-ROM [available only with the book].
In the United States the formation of renal stones (nephrolithiasis) occurs with an annual incidence of 7–21 per 10,000. Nephrolithiasis is complicated by obstruction, infection, and severe pain; and 5–10% of all cases may require hospitalization. Studies of the natural history of this disease show that 50% of patients will have a recurrence in 5 years. Seventy percent of stones are calcium oxalate, and idiopathic hypercalciuria is an important, common risk factor for the formation of stones.
Previous studies have shown that a low calcium intake reduces urinary calcium excretion but can cause a deficiency of calcium and an increase in urinary oxalate. A low animal protein and low-salt diet decreases urinary excretion of calcium and oxalate and may lower the endogenous synthesis of oxalate. Borghi and colleagues (2002) compared the efficacy of a traditional low-calcium diet with a diet containing a normal amount of calcium but reduced amounts of animal protein and salt in the prevention of recurrent stone formation. They enrolled 120 men with idiopathic hypercalciuria and a history of recurrent formation of calcium oxalate stones on at least two occasions in a 5-year randomized trial. One group consisting of 60 men consumed a diet containing a normal amount of calcium (30 mmol/day) but reduced amounts of animal protein and salt. The other group of 60 men followed a traditional low-calcium diet that contained 10 mmol calcium/day. Twenty-four hour urine collections were obtained at baseline, 1 week after randomization, and at yearly intervals; they were used to estimate liquid consumption, and salt, total protein, and animal protein intake. Calcium and oxalate excretion were measured. Renal ultrasound and abdominal flat-plate examinations were performed at yearly intervals. The primary outcome measure was the time to the first recurrence of symptomatic renal stone or presence of radiographically identified stone. Recurrences were classified as either silent or symptomatic. We will use data from this study to illustrate Kaplan–Meier analysis to determine the cumulative incidence of recurrent stones; data are in a file on the CD-ROM [available only with the book] called “Borghi.”
Prostate-specific antigen (PSA) is a serine protease glycoprotein secreted by both normal and neoplastic prostate epithelia. It circulates in the bloodstream and can be measured by a variety of assays and consequently has become an important tool in the understanding of prostate cancer biology and growth. PSA value correlates with the stage of the prostate tumor at diagnosis and is an important prognostic variable. (See also Shipley et al, 1999, Presenting Problem 3 in Chapter 4.) An increasing PSA value after prostate cancer treatment is a sensitive indictor of relapse but does not discriminate between local recurrence and meta static recurrence. Crook and coinvestigators (1997) studied the correlation between both the pretreatment PSA and posttreatment nadir PSA with the outcome in men with localized prostate cancer who were treated with external beam radiation therapy.
This study was a cohort study of 207 men with localized adenocarcinoma of the prostate treated with radiation therapy. Pretreatment PSA values were obtained for all of the men, and posttreatment values were obtained at 3- and 6-month intervals for 5 years and yearly thereafter. Posttreatment prostate biopsies were done at 12 months. Patients with residual tumor had repeat biopsies about every 6 months, whereas those with negative biopsy results had repeat biopsies at 36 months or if a rising PSA value occurred.
The Gleason histologic scoring system was used to classify tumors on a scale of 2 to 10. A low score indicates a well-differentiated tumor, a medium score a moderately differentiated tumor, and a high score a poorly differentiated tumor. Tumors were also classified using the TNM (tumor, node, metastasis) staging system, called the T classification. A T1 tumor is a nonpalpable tumor identified by biopsy. A T2 tumor is palpable on digital rectal examination and limited to the prostate gland. T3 and T4 tumors have invaded adjacent prostate structures, such as the bladder neck or seminal vesicle. The median age of patients was 69 years, and the median duration of follow-up was 36 months. Sixty-eight of the 207 patients had a recurrence of prostate cancer: 20 had local recurrence, 24 had nodal or metastatic recurrence, 7 had both local and distant recurrence, and 17 had biochemical recurrence (elevated PSA with negative biopsy and metastatic workup). The prognostic importance of pretreatment PSA, posttreatment nadir PSA, the Gleason score, and the T classification were examined.
We summarize this study and present the results from the Kaplan–Meier survival analysis predicting recurrence. Data on the patients are given on the CD-ROM [available only with the book] in the data set entitled “Crook.”
Purpose of the Chapter
Many studies in medicine are designed to determine whether a new medication, a new treatment, or a new procedure will perform better than the one in current use. Although measures of short-term effects are of interest with efforts to provide more efficient health care, long-term outcomes, including mortality and major morbidity, are also important. Often, studies focus on comparing survival times for two or more groups of patients.
The methods of data analysis discussed in previous chapters are not appropriate for measuring length of survival for two reasons.
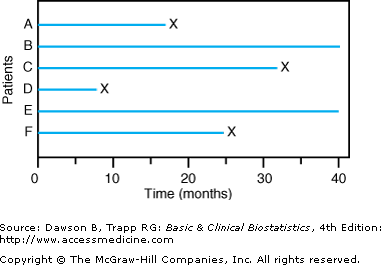
![]() First, investigators frequently must analyze data before all patients have died; otherwise, it may be many years before they know which treatment is better. When analysis of survival is done while some patients in the study are still living, the observations on these patients are called censored observations, because we do not know how long these patients will remain alive. Figure 9–1 illustrates a situation in which observations on patients B and E are censored.
First, investigators frequently must analyze data before all patients have died; otherwise, it may be many years before they know which treatment is better. When analysis of survival is done while some patients in the study are still living, the observations on these patients are called censored observations, because we do not know how long these patients will remain alive. Figure 9–1 illustrates a situation in which observations on patients B and E are censored.
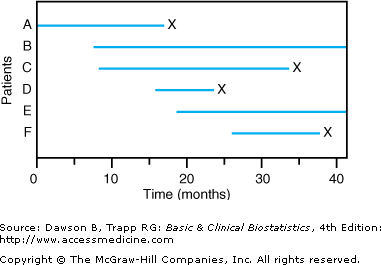
![]() The second reason special methods are needed to analyze survival data is that patients do not typically begin treatment or enter the study at the same time, as they did for Figure 9–1. For example, in the cisplatin study, patients entered the study at different times. When the entry time for patients is not simultaneous and some patients are still in the study when the analysis is done, the data are said to be progressively censored.Figure 9–2 shows results for a study with progressively censored observations. The study began at time 0 months with patient A; then, patient B entered the study at time 7 months; patient C entered at time 8 months; and so on. Patients B and E were still alive at the time the data were analyzed at 40 months.
The second reason special methods are needed to analyze survival data is that patients do not typically begin treatment or enter the study at the same time, as they did for Figure 9–1. For example, in the cisplatin study, patients entered the study at different times. When the entry time for patients is not simultaneous and some patients are still in the study when the analysis is done, the data are said to be progressively censored.Figure 9–2 shows results for a study with progressively censored observations. The study began at time 0 months with patient A; then, patient B entered the study at time 7 months; patient C entered at time 8 months; and so on. Patients B and E were still alive at the time the data were analyzed at 40 months.
Analysis of survival times is sometimes called actuarial, or life table, analysis. Historically, astronomer Edmund Halley (of Halley’s Comet fame) first used life tables in the 17th century to describe survival times of residents of a town. Since then, these methods have been used in various ways. Life insurance companies use them to determine the life expectancy of individuals, and this information is subsequently used to establish premium schedules. Insurers generally use cross-sectional data about how long people of different age groups are expected to live in order to develop a current life table. In medicine, however, most studies of survival use cohort life tables, in which the same group of subjects is followed for a given period. The data for life tables may come from cohort studies (either prospective or historical) or from clinical trials; the key feature is that the same group of subjects is followed for a prescribed time.
In this chapter, we examine two methods to determine survival curves. Actually, it is more accurate to describe them as methods to examine curves with censored data, because many times the outcome is something other than survival. The outcome studied by Borghi and colleagues (2002) was the incidence of stones in patients having idiopathic hypercalciuria who were randomized to one of two diets. Crook and colleagues (1997) studied the recurrence of prostate cancer based on different risk factors.
Why Specialized Methods Are Needed to Analyze Survival Data
Before illustrating the methods for analyzing survival data, let us consider briefly why some intuitive methods are not very useful or appropriate. To illustrate these points, we selected a sample of 26 patients being treated for lung cancer: 13 patients taking irinotecan plus cisplatin and 13 patients taking etoposide plus cisplatin (Table 9–1).
| Row | Case # | Survive | Treatment | Months Survival | Progression Free Survival | Response |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 13.57 | 7.39 | 1 |
| 2 | 3 | 1 | 1 | 11.70 | 4.67 | 1 |
| 3 | 6 | 1 | 1 | 12.52 | 6.64 | 1 |
| 4 | 8 | 1 | 1 | 30.65 | 10.12 | 1 |
| 5 | 9 | 1 | 1 | 2.73 | 1.87 | 0 |
| 6 | 12 | 1 | 1 | 25.49 | 11.14 | 1 |
| 7 | 13 | 1 | 1 | 13.31 | 4.30 | 1 |
| 8 | 14 | 1 | 1 | 16.89 | 7.23 | 1 |
| 9 | 16 | 1 | 1 | 10.94 | 8.02 | 1 |
| 10 | 19 | 1 | 1 | 8.18 | 5.88 | 1 |
| 11 | 20 | 1 | 1 | 9.72 | 8.84 | 1 |
| 12 | 24 | 1 | 1 | 15.61 | 5.75 | 1 |
| 13 | 26 | 1 | 1 | 56.38 | 38.87 | 1 |
| 14 | 2 | 1 | 2 | 8.11 | 8.05 | 1 |
| 15 | 4 | 1 | 2 | 5.82 | 3.12 | 1 |
| 16 | 5 | 1 | 2 | 1.94 | 1.02 | 0 |
| 17 | 7 | 1 | 2 | 13.34 | 3.71 | 1 |
| 18 | 10 | 1 | 2 | 7.56 | 4.40 | 0 |
| 19 | 15 | 1 | 2 | 6.47 | 4.57 | 1 |
| 20 | 17 | 1 | 2 | 14.69 | 11.96 | 1 |
| 21 | 18 | 1 | 2 | 16.26 | 6.54 | 1 |
| 22 | 21 | 1 | 2 | 9.43 | 7.06 | 1 |
| 23 | 22 | 1 | 2 | 9.49 | 8.08 | 1 |
| 24 | 23 | 1 | 2 | 4.86 | 2.76 | 1 |
| 25 | 25 | 1 | 2 | 14.65 | 4.67 | 1 |
| 26 | 28 | 1 | 2 | 5.95 | 2.40 | 1 |
![]() Colton (1974, pp. 238–241) gives a creative presentation of some simple methods to analyze survival data; the arguments presented in this section are modeled on his discussion. Some methods appear at first glance to be appropriate for analyzing survival data, but closer inspection shows they are incorrect.
Colton (1974, pp. 238–241) gives a creative presentation of some simple methods to analyze survival data; the arguments presented in this section are modeled on his discussion. Some methods appear at first glance to be appropriate for analyzing survival data, but closer inspection shows they are incorrect.
Suppose someone suggests calculating the mean length of time patients survive with small-cell lung cancer. Using the data on 26 patients in Table 9–1, the mean survival time for patients on irinotecan plus cisplatin is 17.51 months, and, for patients on etoposide plus cisplatin, 9.12 months. The problem is that mean survival time depends on when the data are analyzed; it will change with each passing month until the point when all the subjects have died. Therefore, mean survival estimates calculated in this way are useful only when all the subjects have died or the event being analyzed has occurred. Almost always, however, investigators wish to analyze their data prior to that time.
An estimate of median length of survival time is also possible, and it can be calculated after only half of the subjects have died. Again, however, investigators often wish to evaluate the outcome prior to that time.
A concept sometimes used in epidemiology is the number of deaths per each 100 person-years of observation. To illustrate, we use the observations in Table 9–1 to determine the number of person-months of survival. Regardless of whether patients are alive or dead at the end of the study, they contribute to the calculation for however long they have been in the study. Patient 1 therefore contributes 13.57 months, patient 2 is in the study for 11.70 days, and so on. The total number of months patients have been observed is 346.25 months; converting to years by dividing by 12 gives 28.8 person-years.
One problem with using person-years of observation is that the same number is obtained by observing 1000 patients for 1 year or by observing 100 patients for 10 years. Although the number of subjects is involved in the calculation of person-years, it is not evident as an explicit part of the result; and no statistical methods are available to compare these numbers. Another problem is the inherent assumption that the risk of an event, such as death or rejection, during any one unit of time is constant throughout the study (although several other survival methods also make this assumption).
Mortality rates (see Chapter 3) are a familiar way to deal with survival data, and they are used (especially in oncology) to estimate 3- and 5-year survival with various types of medical conditions. We cannot determine a mortality rate using data on all patients until the specified length of time has passed.
Suppose we have a study with 20 patients: 10 lived at least 1 year, and 4 died prior to 1 year, and 6 had been in the study less than a year (ie, they were censored). We have to decide what to do with the six censored patients in order to calculate a 1-year survival rate. One solution is to divide the number who died in the first year, 4, by the total number in the study, 20, for an estimate of 0.20, or 20%. This estimate, however, is probably too low, because it assumes that none of the six patients in the study less than 1 year will die before the year is up.
An alternative solution is to ignore the patients who were not in the study for 1 year to obtain 4/(20 – 6) = 0.286, or 28.6%. This technique is similar to the approach used in cancer research in which 3- and 5-year mortality rates are based on only those patients who were in the study at least 3 or 5 years. The shortcoming of this approach is that it ignores completely the contribution of the six patients who were in the study for part of a year. We need a way to use information gained from all patients who entered the study. A reasonable approach should produce an estimate between 20% and 28.6%, which is exactly what actuarial life table analysis and Kaplan–Meier product limit methods do. They give credit for the amounts of time subjects survived up to the time when the data are analyzed.
Actuarial, or Life Table, Analysis
Actuarial, or life table, analysis is also sometimes referred to in the medical literature as the Cutler–Ederer method (1958). The actuarial method is not computationally overwhelming and, at one time, was the predominant method used in medicine. The availability of computers makes it far less often used today, however, than the Kaplan–Meier product limit method discussed in the next section.
![]() We briefly illustrate the calculations involved in actuarial analysis by arranging the 13 patients on etoposide plus cisplatin according to the length of time they had no progression of their disease (Table 9–2). We use the observations in Table 9–2 to produce Table 9–3. The time intervals are arbitrary but should be selected so that the number of censored observations in any interval is small; we group by 3-month intervals.
We briefly illustrate the calculations involved in actuarial analysis by arranging the 13 patients on etoposide plus cisplatin according to the length of time they had no progression of their disease (Table 9–2). We use the observations in Table 9–2 to produce Table 9–3. The time intervals are arbitrary but should be selected so that the number of censored observations in any interval is small; we group by 3-month intervals.
| Filter | trt_arm=2 | ||||
|---|---|---|---|---|---|
| Row | Case # | Survive | Treatment | Progression-Free Survival | Response |
| 1 | 5 | 1 | 2 | 1.02 | 0 |
| 3 | 28 | 1 | 2 | 2.40 | 1 |
| 4 | 23 | 1 | 2 | 2.76 | 1 |
| 5 | 4 | 1 | 2 | 3.12 | 1 |
| 6 | 7 | 1 | 2 | 3.71 | 1 |
| 8 | 10 | 1 | 2 | 4.40 | 0 |
| 9 | 15 | 1 | 2 | 4.57 | 1 |
| 11 | 25 | 1 | 2 | 4.67 | 1 |
| 14 | 18 | 1 | 2 | 6.54 | 1 |
| 16 | 21 | 1 | 2 | 7.06 | 1 |
| 20 | 2 | 1 | 2 | 8.05 | 1 |
| 21 | 22 | 1 | 2 | 8.08 | 1 |
| 25 | 17 | 1 | 2 | 11.96 | 1 |
| Life Table Survival Variable: Progression-Free Survival | |||||||
|---|---|---|---|---|---|---|---|
| ni | wi | di | qi = di/[ni–(wi/2)] | pi = 1–qi | si= pipi–1pi–2… p1 | ||
| Interval Start Time | Number Entering this Interval | Number Withdrawn During Interval | Number Exposed to Risk | Number of Terminal Events | Propn Terminating | Propn Surviving | Cumul Propn Surv at End |
| 0.0 | 13.0 | 2.0 | 12.0 | 1.0 | 0.833 | 0.9167 | 0.9167 |
| 3.0 | 10.0 | 4.0 | 8.0 | 1.0 | 0.1250 | 0.8750 | 0.8021 |
| 6.0 | 5.0 | 4.0 | 3.0 | 0.0 | 0.0000 | 1.0000 | 0.8021 |
| 9.0 | 1.0 | 1.0 | 0.5 | 0.0 | 0.0000 | 1.0000 | 0.8021 |
The column headed ni in Table 9–3 is the number of patients in the study at the beginning of the interval; all patients (13) began the study, so n1 is 13. Three patients did not complete the first time interval: patients 5, 28, 23. Of these, one patient’s disease progressed (patient 5), referred to as a terminal event (d1); the remaining two patients are referred to as withdrawals (w1).
![]() The actuarial method assumes that patients withdraw randomly throughout the interval; therefore, on the average, they withdraw halfway through the time represented by the interval. In a sense, this method gives patients who withdraw credit for being in the study for half of the period. One-half of the number of patients withdrawing is subtracted from the number beginning the interval, so the denominator used to calculate the proportion having a terminal event is reduced by half of the number who withdraw during the period, 13 – (1⁄2 × 2), or 12 in our example. The proportion terminating is 1/12 = 0.0833. The proportion surviving is 1 – 0.0833 = 0.9167, and, because we are still in the first period, the cumulative survival is also 0.9167.
The actuarial method assumes that patients withdraw randomly throughout the interval; therefore, on the average, they withdraw halfway through the time represented by the interval. In a sense, this method gives patients who withdraw credit for being in the study for half of the period. One-half of the number of patients withdrawing is subtracted from the number beginning the interval, so the denominator used to calculate the proportion having a terminal event is reduced by half of the number who withdraw during the period, 13 – (1⁄2 × 2), or 12 in our example. The proportion terminating is 1/12 = 0.0833. The proportion surviving is 1 – 0.0833 = 0.9167, and, because we are still in the first period, the cumulative survival is also 0.9167.
At the beginning of the second interval, only ten patients remain. During the second period, four patients withdrew and one’s disease progressed (patient 10), so d2 = 1 and w2 = 4. The proportion terminating at the second interval is not 1/10 because, although ten patients began the interval, four patients withdrew giving 10 – 2 for the denominator. In our example, the proportion terminating during the second period is 1/[10 – (4/2)] = 1/8, or 0.1250. Again, the proportion with no progression is 1 – 0.1250, or 0.8750, and the cumulative proportion is 0.0.9167 × 0.8750, or 0.8021. This computation procedure continues until the table is completed.
Note that pi is the probability of surviving interval i only; and to survive interval i, a patient must have survived all previous intervals as well. Thus, pi is an example of a conditional probability because the probability of surviving interval i is dependent, or conditional, on surviving until that point. This probability is sometimes called the survival function. Recall from Chapter 4 that if one event is conditional on a previous event, the probability of their joint occurrence is found by multiplying the probability of the conditional event by the probability of the previous event. The cumulative probability of surviving interval i plus all previous intervals is therefore found by multiplying pi by pi–1, pi–2, . . p1.
The results from an actuarial analysis can help answer questions that may help clinicians counsel patients or their families. For example, we might ask, If X is the length of time survived by a patient selected at random from the population represented by these patients, what is the probability that X is 6 months or greater? From Table 9–3, the probability is 0.80, or 4 out of 5, that a patient will live for at least 6 months.
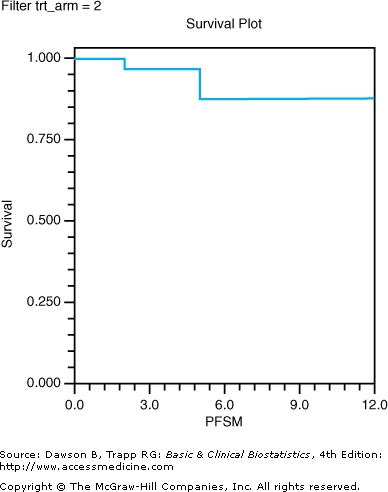
Journal articles rarely present the results from life table analysis as we have in Table 9–3; rather, the results are usually presented in a survival curve. The line in Figure 9–3 is a survival curve for the sample of 13 patients on etoposide plus cisplatin.
Figure 9–3.
Life table survival plot of a sample of patients in the etoposide plus cisplatin arm. (Data, used with permission, from Noda K, Nishiwaki Y, Kawahara M, Negoro S, Sugiura T, Yokoyama A, et al: Irinotecan plus cisplatin compared with etoposide plus cisplatin for extensive small-cell lung cancer. N Engl J Med 2002;346:85–91. Survival plot produced with NCSS, used with permission.)
The actuarial method involves two assumptions about the data. The first is that all withdrawals during a given interval occur, on average, at the midpoint of the interval. This assumption is of less consequence when short time intervals are analyzed; however, considerable bias can occur if the intervals are large, if many withdrawals occur, and if withdrawals do not occur midway in the interval. The Kaplan–Meier method introduced in the next section overcomes this problem. The second assumption is that, although survival in a given period depends on survival in all previous periods, the probability of survival at one period is treated as though it is independent of the probability of survival at others. This condition, although probably violated somewhat in much medical research, does not appear to cause major concern to biostatisticians.
Kaplan–Meier Product Limit Method
![]() The Kaplan–Meier method of estimating survival is similar to actuarial analysis except that time since entry in the study is not divided into intervals for analysis. Depending on the number of patients who died, the Kaplan–Meier product limit method, commonly called Kaplan–Meier curves, may involve fewer calculations than the actuarial method, primarily because survival is estimated each time a patient dies, so withdrawals are ignored. We will illustrate with data from Noda and colleagues (2002) using the same subset of patients as with life table analysis, patients on etoposide plus cisplatin.
The Kaplan–Meier method of estimating survival is similar to actuarial analysis except that time since entry in the study is not divided into intervals for analysis. Depending on the number of patients who died, the Kaplan–Meier product limit method, commonly called Kaplan–Meier curves, may involve fewer calculations than the actuarial method, primarily because survival is estimated each time a patient dies, so withdrawals are ignored. We will illustrate with data from Noda and colleagues (2002) using the same subset of patients as with life table analysis, patients on etoposide plus cisplatin.
The first step is to list the times when a death or dropout occurs, as in the column “Event Time” in Table 9–4
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree