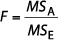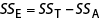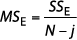Key Concepts
 Special statistical tests are needed when more than two groups are studied or when a group is measured on several variables.
Special statistical tests are needed when more than two groups are studied or when a group is measured on several variables.
 Analysis of variance, or ANOVA, is a statistical method that divides the variance in an observation into the variance among groups and the rest of the variance, called the within-group or error variance.
Analysis of variance, or ANOVA, is a statistical method that divides the variance in an observation into the variance among groups and the rest of the variance, called the within-group or error variance.
 The F test used to compare two variances in Chapter 6 is used to compare the variance among groups to the error.
The F test used to compare two variances in Chapter 6 is used to compare the variance among groups to the error.
 An example of the way ANOVA is calculated from the definitional formulas is helpful in understanding the logic behind the test.
An example of the way ANOVA is calculated from the definitional formulas is helpful in understanding the logic behind the test.
 The terms used in ANOVA are important, but the details of the computations are given for illustration only, and computer programs are used for all ANOVA procedures.
The terms used in ANOVA are important, but the details of the computations are given for illustration only, and computer programs are used for all ANOVA procedures.
 One-way ANOVA is the appropriate method when more than two groups are studied on one variable.
One-way ANOVA is the appropriate method when more than two groups are studied on one variable.
 As with the t test, certain assumptions must be made to use ANOVA, and equal variances is one of the most important.
As with the t test, certain assumptions must be made to use ANOVA, and equal variances is one of the most important.
 Making many comparisons among groups increases the chances of a type I error, that a difference is concluded when there is none.
Making many comparisons among groups increases the chances of a type I error, that a difference is concluded when there is none.
 Investigators can decide ahead of time what specific comparisons they want to make.
Investigators can decide ahead of time what specific comparisons they want to make.
 The Bonferroni procedure is a common way to compensate for making many comparisons among groups; it works by reducing the size of α for each comparison, essentially increasing the difference needed to be significant.
The Bonferroni procedure is a common way to compensate for making many comparisons among groups; it works by reducing the size of α for each comparison, essentially increasing the difference needed to be significant.
 Some multiple comparison methods, called post hoc, are done only if the ANOVA results are statistically significant.
Some multiple comparison methods, called post hoc, are done only if the ANOVA results are statistically significant.
 Tukey’s test is one of the most highly recommended post hoc tests for comparing mean differences.
Tukey’s test is one of the most highly recommended post hoc tests for comparing mean differences.
 The Scheffé post hoc test is the most conservative (requiring a larger difference to be significant), but it is also the most versatile.
The Scheffé post hoc test is the most conservative (requiring a larger difference to be significant), but it is also the most versatile.
 The Newman–Kuels post hoc test is used frequently in basic science research.
The Newman–Kuels post hoc test is used frequently in basic science research.
 Dunnett’s procedure is the test of choice if the only comparisons being made are between the mean in a control group and the means in other groups.
Dunnett’s procedure is the test of choice if the only comparisons being made are between the mean in a control group and the means in other groups.
 Two-way ANOVA analyzes two factors instead of just one, as in one-way ANOVA. It also permits the analysis of the interaction between two factors.
Two-way ANOVA analyzes two factors instead of just one, as in one-way ANOVA. It also permits the analysis of the interaction between two factors.
 ANOVA designs involving more that two factors are possible, generally called factorial designs.
ANOVA designs involving more that two factors are possible, generally called factorial designs.
 Confounding variables can be accommodated by the ANOVA randomized block design.
Confounding variables can be accommodated by the ANOVA randomized block design.
 Repeated-measures ANOVA is a common procedure in medical research; it is analogous to the paired t test with more than two groups and is also called the split-plot design.
Repeated-measures ANOVA is a common procedure in medical research; it is analogous to the paired t test with more than two groups and is also called the split-plot design.
 Nonparametric ANOVA methods include Kruskal–Wallis for one-way designs and Friedman two-way ANOVA for repeated measures. These methods are analogous to the Wilcoxon procedures and are used when the assumptions for ANOVA are not met.
Nonparametric ANOVA methods include Kruskal–Wallis for one-way designs and Friedman two-way ANOVA for repeated measures. These methods are analogous to the Wilcoxon procedures and are used when the assumptions for ANOVA are not met.
 The chi-square test can be used to compare more than two proportions and to determine if there is an association between two factors, each of which can have two or more levels. It is a simple extension of the chi-square test we discussed in Chapter 6.
The chi-square test can be used to compare more than two proportions and to determine if there is an association between two factors, each of which can have two or more levels. It is a simple extension of the chi-square test we discussed in Chapter 6.
 As with research questions involving one or two groups, power analysis is important for studies that use ANOVA. The calculations become increasingly complex, but statistical power programs are available to cover many of the designs.
As with research questions involving one or two groups, power analysis is important for studies that use ANOVA. The calculations become increasingly complex, but statistical power programs are available to cover many of the designs.
Presenting Problems
The usual treatment of hypothyroidism involves daily thyroid replacement with levothyroxine (l–T4). Optimal therapy is monitored by measurement of serum TSH—the elevated level present in the hypothyroid state generally returns to normal over a period of several months. The normal thyroid gland secretes both levothyroxine (l-T4) and levotriiodothyronine (l-T3). About 25% of circulating T3 is secreted by the thyroid gland, and the remainder is produced by peripheral conversion from T4. It is generally believed that treatment with l-T4 alone results in normal levels of serum l-T3 to achieve a euthyroid state. Some studies suggest, however, that patients feel better when taking an l-T4/l-T3 combination compared with l-T4 alone.
Woeber (2002) wished to study this clinical issue further by evaluating the effect of l–T4 replacement therapy on serum free T4 and free T3 concentrations. He studied the relationship between serum free T4 and free T3 concentrations in a historical cohort of patients with chronic autoimmune thyroiditis and a group of normal individuals. Of the 53 patients with thyroiditis characterized by the presence of thyroperoxidase antibodies, 18 had normal serum TSH values and were not taking l-T4 replacement, and 35 were taking l-T4 replacement therapy for hypothyroidism and had normal TSH values. He also studied 20 individuals with normal serum TSH levels who served as the control group. We will use the data from his study to illustrate the use of one-way analysis of variance to decide if the mean values are different in the three groups of subjects.
Previous studies of hyperthyroid patients have demonstrated impaired glucose tolerance and hypersecretion of insulin, supporting the concept of insulin resistance or diminished insulin sensitivity in hyperthyroidism. Published data on insulin sensitivity in hyperthyroidism conflict, however, and both diminished and normal insulin-stimulated glucose use are reported. Although most patients with hyperthyroidism lose weight, some women with this disease are slightly overweight. The association between obesity and decreased insulin sensitivity is well known. Gonzalo and colleagues (1996) studied the effect of excess body weight on glucose tolerance, insulin secretion, and insulin sensitivity in hyperthyroid patients. Intravenous glucose tolerance tests were performed on 14 hyperthyroid women, 6 of whom were overweight, and in 19 volunteers with normal thyroid levels matched for age and weight.a
aThe term matching generally means that one patient is matched with the control subject to ensure the groups are similar on the matching variable. Sometimes, two control subjects are selected for each patient. Fourteen patients and 19 controls were included in this study, and we expect the authors meant that the controls were selected so that the overall age and BMI distributions were similar to those in the patients.
The investigators wanted to know if differences existed in various outcomes depending on thyroid level and body mass index. We use the measurement on insulin sensitivity to illustrate the use of two-way analysis of variance. Data are given in the section titled, “Two-Way ANOVA: Factorial Design,” and are in a folder entitled “Gonzalo” on the CD-ROM [available only with the book].
Arthrodesis (fusion) of the first metatarsophalangeal (MTP) joint of the foot is a common surgical procedure used for treating severe pain caused by hallux valgus, hallux rigidus, and advanced rheumatoid forefoot deformity. Hallux valgus is a condition in which the large toe deviates laterally and the first metatarsal head deviates medially, causing bunion deformity. Hallux rigidus is characterized by aching pain in the great toe and marked restriction of movement in the first MTP joint.
Lombardi and his coinvestigators (2002) examined the radiographic records of 48 patients (54 feet) who had undergone first MTP arthrodesis for hallux rigidus (group A), hallux valgus (group B), or rheumatoid forefoot deformity (group C). They studied the effect of first MTP joint arthrodesis, in which the joint is fused in a dorsiflexed position, on the sagittal position of the first toe and the medial longitudinal arch by taking five different angular measurements on each patient’s preoperative and postoperative weight-bearing lateral radiographs. These measurements included: first metatarsal declination (MD), talometatarsal (TM), talar declination (TD), calcaneal inclination (CI), and talocalcaneal (TC). The investigators wanted to know whether there were changes with surgery and, if so, whether the changes were the same for all three groups. The study is discussed in the section titled, “Repeated-Measures Designs,” and data are on the CD-ROM [available only with the book].
Purpose of the Chapter
![]() Many research projects in medicine employ more than two groups, and the chi-square tests discussed in Chapter 6 can be extended for three or more groups when the outcome is a categorical (or counted) measure. When the outcome is numerical, means are used, and the t tests discussed in Chapters 5 and 6 are applicable only for the comparison of two groups. Other studies examine the influence of more than one factor. These situations call for a global, or omnibus, test to see whether any differences exist in the data prior to testing various combinations of means to determine individual group differences.
Many research projects in medicine employ more than two groups, and the chi-square tests discussed in Chapter 6 can be extended for three or more groups when the outcome is a categorical (or counted) measure. When the outcome is numerical, means are used, and the t tests discussed in Chapters 5 and 6 are applicable only for the comparison of two groups. Other studies examine the influence of more than one factor. These situations call for a global, or omnibus, test to see whether any differences exist in the data prior to testing various combinations of means to determine individual group differences.
If a global test is not performed, multiple tests between different pairs of means will alter the significance or α level for the experiment as a whole rather than for each comparison. For example, Marwick and colleagues (1999) studied the relationship between myocardial profusion imaging and cardiac mortality in men and women. Factors included the number of involved coronary vessels (zero to three) and whether the profusion defect was fixed or could be reversed. Had these investigators not properly used multivariate methods to analyze the data, methods we discuss in Chapter 10, comparing men and women on the 4 × 2 different combinations of these factors would produce eight P values. If each comparison is made by using α = 0.05, the chance that each comparison will falsely be called significant is 5%; that is, a type I error may occur eight different times. Overall, therefore, the chance (8 × 5%) of declaring one of the comparisons incorrectly significant is 40%.b
bActually, 40% is only approximately correct; it does not reflect the fact that some of the comparisons are not independent.
One approach for analyzing data that include multiple observations is called the analysis of variance, abbreviated ANOVA or anova. This method protects against error “inflation” by first asking if any differences exist at all among means of the groups. If the result of the ANOVA is significant, the answer is yes, and the investigator then makes comparisons among pairs or combinations of groups.
The topic of analysis of variance is complex, and many textbooks are devoted to the subject. Its use in the medical literature is somewhat limited, however, because regression methods (see Chapter 10) can be used to answer the same research questions. Our goal is to provide enough discussion so that you can identify situations in which ANOVA is appropriate and interpret the results. If you are interested in learning more about analysis of variance, consult Berry and coworkers (2001) or the still classic text by Dunn and Clark (1987). Except for simple study designs, our advice to researchers conducting a study that involves more than two groups or two or more variables is to consult a statistician to determine how best to analyze the data.
Intuitive Overview of ANOVA
In Presenting Problem 1, serum free l–T4 levels were measured in three groups of subjects: group A (20 control individuals) and groups B and C (hypothyroid patients who were or were not on therapy). The original observations, sample sizes, means, and standard deviations are reproduced in Table 7–1 from the original Table 2 in Woeber (2002).
![]() ANOVA provides a way to divide the total variation in serum free T4 levels of each subject into two parts. Suppose we denote a given subject’s free T4 as X and consider how much X differs from the mean T4 for all the subjects in the study, abbreviated
ANOVA provides a way to divide the total variation in serum free T4 levels of each subject into two parts. Suppose we denote a given subject’s free T4 as X and consider how much X differs from the mean T4 for all the subjects in the study, abbreviated  . This difference (symbolized X –
. This difference (symbolized X – 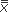 ) can be divided into two parts: the difference between X and the mean of the group this subject is in,
) can be divided into two parts: the difference between X and the mean of the group this subject is in, 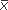 j, and the difference between the group mean and the grand mean. In symbols, we write
j, and the difference between the group mean and the grand mean. In symbols, we write
Table 7–2 contains the original observations for the subjects in the study. Subject 1 in the control group has a free T4 of 15 pmol/L. The grand mean for all subjects is 14.78, so subject 1 differs from the grand mean by 15 –14.78, or 0.22. This difference can be divided into two parts: the difference between 15 and the mean for the control group, 13.55; and the difference between the mean for the normal group and the grand mean. Thus
| Group A: Controls (n=20) | Group B: Normal Patients (n=18) | Group C: Patients on Therapy (n=35) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Subject | FT4 | FT3 | FT4/FT3 | FT4 | FT3 | FT4/FT3 | FT4 | FT3 | FT4/FT3 |
| 1 | 15 | 3.9 | 3.8 | 14 | 4.5 | 3.1 | 15 | 3.7 | 4.1 |
| 2 | 14 | 4.9 | 2.9 | 13 | 4.0 | 3.3 | 13 | 3.1 | 4.2 |
| 3 | 14 | 3.9 | 3.6 | 21 | 5.2 | 4.0 | 17 | 3.7 | 4.6 |
| 4 | 13 | 3.7 | 3.5 | 14 | 4.1 | 3.4 | 17 | 4.0 | 4.3 |
| 5 | 12 | 4.8 | 2.5 | 14 | 4.5 | 3.1 | 15 | 3.3 | 4.5 |
| 6 | 15 | 4.1 | 3.7 | 13 | 4.1 | 3.2 | 15 | 3.8 | 3.9 |
| 7 | 12 | 4.5 | 2.7 | 14 | 3.9 | 3.6 | 14 | 3.4 | 4.1 |
| 8 | 13 | 4.2 | 3.1 | 15 | 3.9 | 3.8 | 18 | 4.7 | 3.8 |
| 9 | 11 | 3.9 | 2.8 | 12 | 4.0 | 3.0 | 14 | 4.1 | 3.4 |
| 10 | 14 | 5.7 | 2.5 | 12 | 5.1 | 2.4 | 17 | 3.7 | 4.6 |
| 11 | 11 | 4.3 | 2.6 | 14 | 4.3 | 3.3 | 20 | 4.0 | 5.0 |
| 12 | 12 | 3.8 | 3.2 | 15 | 4.5 | 3.3 | 16 | 3.8 | 4.2 |
| 13 | 15 | 4.1 | 3.7 | 14 | 3.7 | 3.8 | 15 | 4.4 | 3.4 |
| 14 | 15 | 3.4 | 4.4 | 15 | 5.0 | 3.0 | 15 | 4.1 | 3.7 |
| 15 | 14 | 4.4 | 3.2 | 13 | 5.4 | 2.4 | 14 | 4.1 | 3.4 |
| 16 | 16 | 4.2 | 3.8 | 12 | 4.2 | 2.9 | 17 | 3.6 | 4.7 |
| 17 | 13 | 4.3 | 3.0 | 15 | 5.0 | 3.0 | 18 | 4.2 | 4.3 |
| 18 | 14 | 4.2 | 3.3 | 12 | 3.6 | 3.3 | 19 | 4.3 | 4.4 |
| 19 | 13 | 4.3 | 3.0 | 15 | 3.7 | 4.1 | |||
| 20 | 15 | 4.1 | 3.7 | 16 | 4.6 | 3.5 | |||
| 21 | 16 | 4.3 | 3.7 | ||||||
| 22 | 20 | 4.3 | 4.7 | ||||||
| 23 | 16 | 4.2 | 3.8 | ||||||
| 24 | 18 | 3.7 | 4.9 | ||||||
| 25 | 17 | 5.3 | 3.2 | ||||||
| 26 | 14 | 4.2 | 3.3 | ||||||
| 27 | 16 | 3.1 | 5.2 | ||||||
| 28 | 18 | 4.1 | 4.4 | ||||||
| 29 | 15 | 4.9 | 3.1 | ||||||
| 30 | 13 | 3.6 | 3.6 | ||||||
| 31 | 14 | 4.3 | 3.3 | ||||||
| 32 | 12 | 4.9 | 2.4 | ||||||
| 33 | 16 | 3.9 | 4.1 | ||||||
| 34 | 18 | 3.9 | 4.6 | ||||||
| 35 | 13 | 3.6 | 3.6 | ||||||
| Group Mean | 13.55 | 4.24 | 3.24 | 14.00 | 4.39 | 3.21 | 15.89 | 4.02 | 4.00 |
| Group standard deviation | 1.43 | 0.49 | 0.52 | 2.06 | 0.55 | 0.44 | 2.00 | 0.50 | 0.61 |
| Overall Mean | 14.78 | 4.17 | 3.60 | ||||||
| Overall standard deviation | 2.14 | 0.52 | 0.67 | ||||||
Although our example does not show exactly how ANOVA works, it illustrates the concept of dividing the variation into different parts. Here, we were looking at simple differences related to just one observation; ANOVA considers the variation in all observations and divides it into (1) the variation between each subject and the subject’s group mean and (2) the variation between each group mean and the grand mean. If the group means are quite different from one another, considerable variation will occur between them and the grand mean, compared with the variation within each group. If the group means are not very different, the variation between them and the grand mean will not be much more than the variation among the subjects within each group. The F test for two variances (Chapter 6) can be used to test the ratio of the variance among means to the variance among subjects within each group.
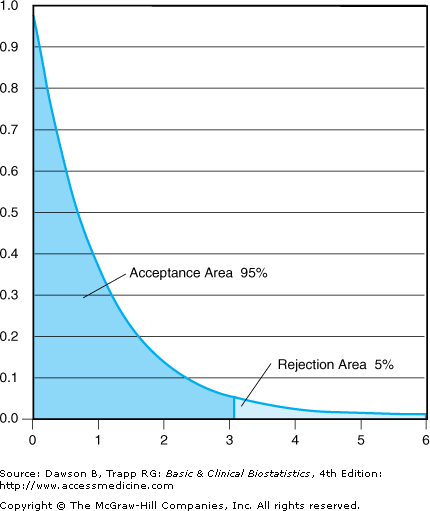
![]() The null hypothesis for the F test is that the two variances are equal; if they are, the variation among means is not much greater than the variation among individual observations within any given group. In this situation, we cannot conclude that the means are different from one another. Thus, we think of ANOVA as a test of the equality of means, even though the variances are being tested in the process. If the null hypothesis is rejected, we conclude that not all the means are equal; however, we do not know which ones are not equal, which is why post hoc comparisonprocedures are necessary.
The null hypothesis for the F test is that the two variances are equal; if they are, the variation among means is not much greater than the variation among individual observations within any given group. In this situation, we cannot conclude that the means are different from one another. Thus, we think of ANOVA as a test of the equality of means, even though the variances are being tested in the process. If the null hypothesis is rejected, we conclude that not all the means are equal; however, we do not know which ones are not equal, which is why post hoc comparisonprocedures are necessary.
![]() Recall that the formula for the variance of the observations (or squared standard deviation; see Chapter 3) involves the sum of the squared deviations of each X from the mean
Recall that the formula for the variance of the observations (or squared standard deviation; see Chapter 3) involves the sum of the squared deviations of each X from the mean  :
:
A similar formula can be used to find the variance of means from the grand mean:
where nj is the number of observations in each group and j is the number of groups. This estimate is called the mean square among groups, abbreviated MSA, and it has j – 1 degrees of freedom.
To obtain the variance within groups, we use a pooled variance like the one for the t test for two independent groups:
This estimate is called the error mean square (or mean square within), abbreviated MSE. It has Σ(nj – 1) degrees of freedom, or, if the sum of the number of observations is denoted by N, N – j degrees of freedom. The F ratio is formed by dividing the estimate of the variance of means (mean square among groups) by the estimate of the variance within groups (error mean square), and it has j – 1 and N – j degrees of freedom.
We will use the data from the study by Woeber (2002) to illustrate the calculations. In this example, the outcome of interest (free T4) is the dependent variable, and the grouping variable (control subjects and two sets of patients) is the independent variable. The data in Table 7–1 indicate that the mean free T4 for group C, the patients on therapy for hypothyroidism, is higher than the means for the other two groups. If these three groups of subjects are viewed as coming from a larger population, then the question is whether free T4 levels differ in the population. Although differences exist in the means in Table 7–1, some differences in the samples would occur simply by chance, even when no variation exists in the population. So, the question is reduced to whether the observed differences are large enough to convince us that they did not occur merely by chance but reflect real distinctions in the population.
The statistical hypothesis being tested, the null hypothesis, is that the mean free T4 is equal among the three groups. The alternative hypothesis is that a difference does exist; that is, not all the means are equal. The steps in testing the null hypothesis follow.
Step 1: H0: The mean free T4 is equal in the three groups, or, in symbols, μ1 = μ2 = μ3
H1: The means are not equal, or, in symbols, μ1 ≠ μ2 or μ2 ≠ μ3 or μ1 ≠ μ3
Step 2: The test statistic in the test of equality of means in ANOVA is the F ratio, F = MSA/MSE, with j – 1 and Σ (nj – 1) degrees of freedom.
Step 3:We use α = 0.05 for this statistical test.
Step 4:The value of the F distribution from Table A–4 with j – 1 = 2 degrees of freedom in the numerator and Σ (nj – 1) = 70 in the denominator is between 3.15 and 3.07; interpolating gives 3.14. The decision is to reject the null hypothesis of equal means if the observed value of F is greater than 3.14 and falls in the rejection area (Figure 7–1).
Step 5: First we calculate the grand mean. Because we already know the means for the three groups, we can form a weighted average of these means to find the grand mean:
The numerator of the MSA is:
The term MSA, found by dividing the numerator by the number of groups minus 1, (j – 1)—which is 2 in this example, is:
The individual group variances are used to calculate the pooled estimate of the MSE:
Finally, the F ratio is found by dividing the mean square among groups by the error mean square:
Step 6: The observed value of the F ratio is 11.95, which is larger than 3.14 (the critical value from Step 4). The null hypothesis of equal means is therefore rejected. We conclude that a difference does exist in free T4 levels among normal control subjects, hypothyroid patients not on replacement therapy, and patients on replacement therapy. Note that rejecting the null hypothesis does not tell us which group means differ, only that a difference exists; in the section titled, “Multiple-Comparison Procedures,” we illustrate different methods that can be used to learn which specific groups differ.
Traditional Approach to ANOVA
In the preceding section, we presented a simple illustration of ANOVA by using formulas to estimate the variance among individual group means and the grand mean, called the mean square among groups (MSA), and the variance within groups, called the mean square error or mean square within groups (MSE). Traditionally in ANOVA, formulas are given for sums of squares, which are generally equivalent to the numerators of the formulas used in the preceding section; then, sums of squares are divided by appropriate degrees of freedom to obtain mean squares. Before illustrating the calculations for the data on free T4 levels, we define some terms and give the traditional formulas.
![]() In ANOVA, the term factor refers to the variable by which groups are formed, the independent variable. For example, in Presenting Problem 1, subjects were divided into groups based on their thyroid and replacement therapy status; therefore, this study is an example of a one-factor ANOVA, called a one-way ANOVA. The number of groups defined by a given factor is referred to as the number of levels of the factor; the factor in Presenting Problem 1 has three groups, or we say that the group factor has three levels. In experimental studies in medicine, levels are frequently referred to as treatments.
In ANOVA, the term factor refers to the variable by which groups are formed, the independent variable. For example, in Presenting Problem 1, subjects were divided into groups based on their thyroid and replacement therapy status; therefore, this study is an example of a one-factor ANOVA, called a one-way ANOVA. The number of groups defined by a given factor is referred to as the number of levels of the factor; the factor in Presenting Problem 1 has three groups, or we say that the group factor has three levels. In experimental studies in medicine, levels are frequently referred to as treatments.
Some textbooks approach analysis of variance from the perspective of models. The model for one-way ANOVA states that an individual observation can be divided into three components related to (1) the grand mean, (2) the group to which the individual belongs, and (3) the individual observation itself. To write this model in symbols, we let i stand for a given individual observation and j stand for the group to which this individual belongs. Then, Xij denotes the observation of individual i in group j; for example, X11 is the first observation in the first group, and X53 is the fifth observation in the third group. The grand mean in the model is denoted by μ. The effect of being a member of group j may be thought of as the difference between the mean of group j and the grand mean; the effect associated with being in group j is written αj. Finally, the difference between the individual observation and the mean of the group to which the observation belongs is written eij and is called the error term, or residual. Putting these symbols together, we can write the model for one-way ANOVA as
which states that the ith observation in the jth group, Xij, is the sum of three components: the grand mean μ; the effect associated with group j, αj; and an error (residual), eij.
The size of an effect is, of course, related to the size of the difference between a given group mean and the grand mean. When inferences involve only specific levels of the factor included in the study, the model is called a fixed-effects model. The fixed-effects model assumes we are interested in making inferences only to the populations represented in the study, such as occurs, for example, if investigators wish to draw conclusions about three dosage levels of a drug. If, in contrast, the dosage levels included in the study are viewed as being randomly selected from all different possible dosage levels of the drug, the model is called a random-effects model, and inferences can be made to other levels of the factor not represented in the study.c Both models are used to test hypotheses about the equality of group means. The random-effects model, however, can also be used to test hypotheses and form confidence intervals about group variances, and it is also referred to as the components-of-variance model for this reason.
cThe calculations of sums of squares and mean squares are the same in both models, but the type of model determines the way the F ratio is formed when two or more factors are included in a study.
In the section titled, “The Logic of ANOVA,” we showed that the variation of 0.22 pmol/L of free T4 from the grand mean of 14.78 (subject 1 in the control group) can be expressed as a sum of two differences: (1) the difference between the observation and the mean of the group it is in, plus (2) the difference between its group mean and the grand mean. This result is also true when the differences are squared and the squared deviations are added to form the sum of squares.
To illustrate, for one factor with j groups, we use the following definitions:
Then, Σ(Xij – )2, the total sum of squares, or SST, can be expressed as the sum of Σ(Xij –
)2, the total sum of squares, or SST, can be expressed as the sum of Σ(Xij –  j)2, the error sum of squares (SSE) and Σ(
j)2, the error sum of squares (SSE) and Σ(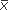 j –
j – 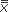 )2, the sum of squares among groups (SSA).
)2, the sum of squares among groups (SSA).
That is,
We do not provide the proof of this equality here, but interested readers can consult any standard statistical reference for more details (eg, Berry, Matthews, Armitage, 2001; Daniel, 1998; Hays, 1997).
Computational formulas are more convenient than definitional formulas when sums of squares are calculated manually or when using calculators, as was the situation before computers were so readily available. Computational formulas are also preferred because they reduce round-off errors. They can be derived from definitional ones, but because the algebra is complex we do not explain it here. If you are interested in the details, consult the previously mentioned texts.
The symbols in ANOVA vary somewhat from one text to another; the following formulas are similar to those used in many books and are the ones we will use to illustrate calculations for ANOVA. Let N be the total number of observations in all the groups, that is, N = Σ nj. Then, the computational formulas for the sums of squares are
and SSE is found by subtraction: SSE = SST – SSA.
The sums of squares are divided by the degrees of freedom to obtain the mean squares:
where j is the number of groups or levels of the factor, and
where j is the number of groups or levels of the factor, and N is the total sample size.
![]() Presenting Problem 1 is an example of a one-way ANOVA model in which there is a numerical independent variable: level of free T4. Three groups of patients are examined: controls, and hypothyroid patients who are taking or not taking replacement therapy; and the mean level of free T4 is examined for subjects in each group. (See Table 7–1.)
Presenting Problem 1 is an example of a one-way ANOVA model in which there is a numerical independent variable: level of free T4. Three groups of patients are examined: controls, and hypothyroid patients who are taking or not taking replacement therapy; and the mean level of free T4 is examined for subjects in each group. (See Table 7–1.)
To calculate sums of squares by using traditional ANOVA formulas, we must obtain three terms:
- 1. We square each observation (Xij) and add, to obtain Σ Xij2.
- 2. We add the observations, square the sum, and divide by N, to obtain (Σ Xij)2/N.
- 3. We square each mean (
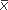 j), multiply by the number of subjects in that group (nj), and add, to obtainΣ nj
j), multiply by the number of subjects in that group (nj), and add, to obtainΣ nj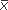 j2.
j2.
These three terms using the data in Table 7–1 are
and
Then, the sums of squares are
Next, the mean squares are calculated.
Slight differences between these results and the results for the mean squares calculated in the section titled, “Illustration of Intuitive Calculations for ANOVA,” are due to round-off error. Otherwise, the results are the same regardless of which formulas are used.
Finally, the F ratio is determined.
The calculated F ratio is compared with the value from the F distribution with 2 and 70 degrees of freedom at the desired level of significance. As we found in the section titled, “Illustration of Intuitive Calculations for ANOVA,” for α = 0.05, the value of F (2, 70) is 3.14. Because 11.93 is greater than 3.14, the null hypothesis is rejected; and we conclude that mean free T4 levels are not the same for patients who have normal thyroid levels (controls), and those who are hypothyroid and either are or are not on replacement therapy. The formulas for one-way ANOVA are summarized in Table 7–3.
![]() Analysis of variance uses information about the means and standard deviations in each group. Like the t test, ANOVA is a parametric method, and some important assumptions are made.
Analysis of variance uses information about the means and standard deviations in each group. Like the t test, ANOVA is a parametric method, and some important assumptions are made.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree