Key Concepts
 Correlation and regression are statistical methods to examine the linear relationship between two numerical variables measured on the same subjects. Correlation describes a relationship, and regression describes both a relationship and predicts an outcome.
Correlation and regression are statistical methods to examine the linear relationship between two numerical variables measured on the same subjects. Correlation describes a relationship, and regression describes both a relationship and predicts an outcome.
 Correlation coefficients range from –1 to +1, both indicating a perfect relationship between two variables. A correlation equal to 0 indicates no relationship.
Correlation coefficients range from –1 to +1, both indicating a perfect relationship between two variables. A correlation equal to 0 indicates no relationship.
 Scatterplots provide a visual display of the relationship between two numerical variables and are recommended to check for a linear relationship and extreme values.
Scatterplots provide a visual display of the relationship between two numerical variables and are recommended to check for a linear relationship and extreme values.
 The coefficient of determination, or r2, is simply the squared correlation; it is the preferred statistic to describe the strength between two numerical variables.
The coefficient of determination, or r2, is simply the squared correlation; it is the preferred statistic to describe the strength between two numerical variables.
 The t test can be used to test the hypothesis that the population correlation is zero.
The t test can be used to test the hypothesis that the population correlation is zero.
 The Fisher z transformation is used to form confidence intervals for the correlation or to test any hypotheses about the value of the correlation.
The Fisher z transformation is used to form confidence intervals for the correlation or to test any hypotheses about the value of the correlation.
 The Fisher z transformation can also be used to form confidence intervals for the difference between correlations in two independent groups.
The Fisher z transformation can also be used to form confidence intervals for the difference between correlations in two independent groups.
 It is possible to test whether the correlation between one variable and a second is the same as the correlation between a third variable and a second variable.
It is possible to test whether the correlation between one variable and a second is the same as the correlation between a third variable and a second variable.
 When one or both of the variables in correlation is skewed, the Spearman rho nonparametric correlation is advised.
When one or both of the variables in correlation is skewed, the Spearman rho nonparametric correlation is advised.
 Linear regression is called linear because it measures only straight-line relationships.
Linear regression is called linear because it measures only straight-line relationships.
 The least squares method is the one used in almost all regression examples in medicine. With one independent and one dependent variable, the regression equation can be given as a straight line.
The least squares method is the one used in almost all regression examples in medicine. With one independent and one dependent variable, the regression equation can be given as a straight line.
 The standard error of the estimate is a statistic that can be used to test hypotheses or form confidence intervals about both the intercept and the regression coefficient (slope).
The standard error of the estimate is a statistic that can be used to test hypotheses or form confidence intervals about both the intercept and the regression coefficient (slope).
 One important use of regression is to be able to predict outcomes in a future group of subjects.
One important use of regression is to be able to predict outcomes in a future group of subjects.
 When predicting outcomes, the confidence limits are called confidence bands about the regression line. The most accurate predictions are for outcomes close to the mean of the independent variable X, and they become less precise as the outcome departs from the mean.
When predicting outcomes, the confidence limits are called confidence bands about the regression line. The most accurate predictions are for outcomes close to the mean of the independent variable X, and they become less precise as the outcome departs from the mean.
 It is possible to test whether the regression line is the same (ie, has the same slope and intercept) in two different groups.
It is possible to test whether the regression line is the same (ie, has the same slope and intercept) in two different groups.
 A residual is the difference between the actual and the predicted outcome; looking at the distribution of residuals helps statisticians decide if the linear regression model is the best approach to analyzing the data.
A residual is the difference between the actual and the predicted outcome; looking at the distribution of residuals helps statisticians decide if the linear regression model is the best approach to analyzing the data.
 Regression toward the mean can result in a treatment or procedure appearing to be of value when it has had no actual effect; having a control group helps to guard against this problem.
Regression toward the mean can result in a treatment or procedure appearing to be of value when it has had no actual effect; having a control group helps to guard against this problem.
 Correlation and regression should not be used unless observations are independent; it is not appropriate to include multiple measurements of the same subjects.
Correlation and regression should not be used unless observations are independent; it is not appropriate to include multiple measurements of the same subjects.
 Mixing two populations can also cause the correlation and regression coefficient to be larger than they should.
Mixing two populations can also cause the correlation and regression coefficient to be larger than they should.
 The use of correlation versus regression should be dictated by the purpose of the research—whether it is to establish a relationship or to predict an outcome.
The use of correlation versus regression should be dictated by the purpose of the research—whether it is to establish a relationship or to predict an outcome.
 The regression model can be extended to accommodate two or more independent variables; this model is called multiple regression.
The regression model can be extended to accommodate two or more independent variables; this model is called multiple regression.
 Determining the needed sample size for correlation and regression is not difficult using one of the power analysis statistical programs.
Determining the needed sample size for correlation and regression is not difficult using one of the power analysis statistical programs.
Presenting Problems
In the United States, according to World Health Organization (WHO) standards, 42% of men and 28% of women are overweight, and an additional 21% of men and 28% of women are obese. Body mass index (BMI) has become the measure to define standards of overweight and obesity. The WHO defines overweight as a BMI between 25 and 29.9 kg/m2 and obesity as a BMI greater than or equal to 30 kg/m2. Jackson and colleagues (2002) point out that the use of BMI as a single standard for obesity for all adults has been recommended because it is assumed to be independent of variables such as age, sex, ethnicity, and physical activity. Their goal was to examine this assumption by evaluating the effects of sex, age, and race on the relation between BMI and measured percent fat. They studied 665 black and white men and women who ranged in age between 17 years and 65 years. Each participant was carefully measured for height and weight to calculate BMI and body density. Relative body fat (%fat) was estimated from body density using previously published equations. The independent variables examined were BMI, sex, age, and race. We examine this data to learn whether a relationship exists, and if so, whether it is linear or not. Data are on the CD [available only with the book] in a folder entitled “Jackson.”
Hypertension, defined as systolic pressure greater than 140 mm Hg or diastolic pressure greater than 90 mm Hg, is present in 20–30% of the U.S. population. Recognition and treatment of hypertension has significantly reduced the morbidity and mortality associated with the complications of hypertension. A number of finger blood pressure devices are marketed for home use by patients as an easy and convenient way for them to monitor their own blood pressure.
How correct are these finger blood pressure devices? Nesselroad and colleagues (1996) studied these devices to determine their accuracy. They measured blood pressure in 100 consecutive patients presenting to a family practice office who consented to participate. After being seated for 5 min, blood pressure was measured in each patient using a standard blood pressure cuff of appropriate size and with each of three automated finger blood pressure devices. The data were analyzed by calculating the correlation coefficient between the value obtained with the blood pressure cuff and the three finger devices and by calculating the percentage of measurements with each automated device that fell within the ± 4 mm Hg margin of error of the blood pressure cuff.
We use the data to illustrate correlation and scatterplots. We also illustrate a test of hypothesis about two dependent or related correlation coefficients. Data are given in the section titled, “Spearman’s Rho,” and on the CD-ROM [available only with the book] in a folder called “Nesselroad.”
Symptoms of forgetfulness and loss of concentration can be a result of natural aging and are often aggravated by fatigue, illness, depression, visual or hearing loss, or certain medications. Hodgson and Cutler (1997) wished to examine the consequences of anticipatory dementia, a phenomenon characterized as the fear that normal and age-associated memory change may be the harbinger of Alzheimer’s disease.
They studied 25 men and women having a living parent with a probable diagnosis of Alzheimer’s disease, a condition in which genetic factors are known to be important. A control group of 25 men and women who did not have a parent with dementia was selected for comparison. A directed interview and questionnaire were used to measure concern about developing Alzheimer’s disease and to assess subjective memory functioning. Four measures of each individual’s sense of well-being were used in the areas of depression, psychiatric symptomatology, life satisfaction, and subjective health status. We use this study to illustrate biserial correlation and show its concordance with the t test. Observations from the study are given in files on the CD-ROM [available only with the book] entitled “Hodgson.”
The study of hyperthyroid women by Gonzalo and coinvestigators (1996) was a presenting problem in Chapter 7. Recall that the study reported the effect of excess body weight in hyperthyroid patients on glucose tolerance, insulin secretion, and insulin sensitivity. The study included 14 hyperthyroid women, 6 of whom were overweight, and 19 volunteers with normal thyroid levels of similar ages and weight. The investigators in this study also examined the relationship between insulin sensitivity and body mass index for hyperthyroid and control women. (See Figure 3 in the Gonzalo article) We revisit this study to calculate and compare two regression lines. Original observations are given in Chapter 7, Table 7–8.
An Overview of Correlation & Regression
In Chapter 3 we introduced methods to describe the association or relationship between two variables. In this chapter we review these concepts and extend the idea to predicting the value of one characteristic from the other. We also present the statistical procedures used to test whether a relationship between two characteristics is significant. Two probability distributions introduced previously, the t distribution and the chi-square distribution, can be used for statistical tests in correlation and regression. As a result, you will be pleased to learn that much of the material in this chapter will be familiar to you.
![]() When the goal is merely to establish a relationship (or association) between two measures, as in these studies, the correlation coefficient (introduced in Chapter 3) is the statistic most often used. Recall that correlation is a measure of the linear relationship between two variables measured on a numerical scale.
When the goal is merely to establish a relationship (or association) between two measures, as in these studies, the correlation coefficient (introduced in Chapter 3) is the statistic most often used. Recall that correlation is a measure of the linear relationship between two variables measured on a numerical scale.
In addition to establishing a relationship, investigators sometimes want to predict an outcome, dependent, or response, variable from an independent, or explanatory, variable. Generally, the explanatory characteristic is the one that occurs first or is easier or less costly to measure. The statistical method of linear regression is used; this technique involves determining an equation for predicting the value of the outcome from values of the explanatory variable. One of the major differences between correlation and regression is the purpose of the analysis—whether it is merely to describe a relationship or to predict a value. Several important similarities also occur as well, including the direct relationship between the correlation coefficient and the regression coefficient. Many of the same assumptions are required for correlation and regression, and both measure the extent of a linear relationship between the two characteristics.
Correlation
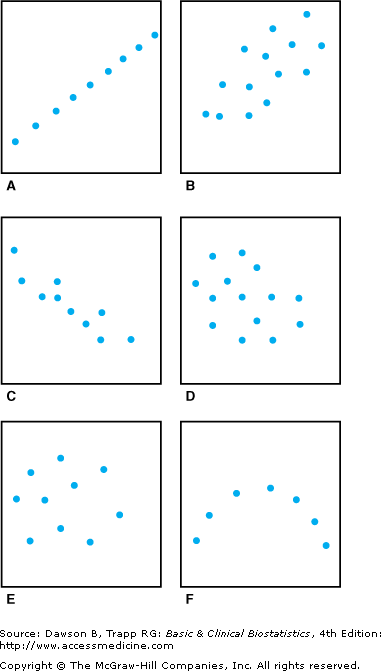
![]() Figure 8–1 illustrates several hypothetical scatterplots of data to demonstrate the relationship between the size of the correlation coefficient r and the shape of the scatterplot. When the correlation is near zero, as in Figure 8–1E, the pattern of plotted points is somewhat circular. When the degree of relationship is small, the pattern is more like an oval, as in Figures 8–1D and 8–1B. As the value of the correlation gets closer to either +1 or –1, as in Figure 8–1C, the plot has a long, narrow shape; at +1 and –1, the observations fall directly on a line, as for r = +1.0 in Figure 8–1A.
Figure 8–1 illustrates several hypothetical scatterplots of data to demonstrate the relationship between the size of the correlation coefficient r and the shape of the scatterplot. When the correlation is near zero, as in Figure 8–1E, the pattern of plotted points is somewhat circular. When the degree of relationship is small, the pattern is more like an oval, as in Figures 8–1D and 8–1B. As the value of the correlation gets closer to either +1 or –1, as in Figure 8–1C, the plot has a long, narrow shape; at +1 and –1, the observations fall directly on a line, as for r = +1.0 in Figure 8–1A.
The scatterplot in Figure 8–1F illustrates a situation in which a strong but nonlinear relationship exists. For example, with temperatures less than 10–15°C, a cold nerve fiber discharges few impulses; as the temperature increases, so do numbers of impulses per second until the temperature reaches about 25°C. As the temperature increases beyond 25°C, the numbers of impulses per second decrease once again, until they cease at 40–45°C. The correlation coefficient, however, measures only a linear relationship, and it has a value close to zero in this situation.
One of the reasons for producing scatterplots of data as part of the initial analysis is to identify nonlinear relationships when they occur. Otherwise, if researchers calculate the correlation coefficient without examining the data, they can miss a strong, but nonlinear, relationship, such as the one between temperature and number of cold nerve fiber impulses.
We use the study by Jackson and colleagues (2002) to extend our understanding of correlation. We assume that anyone interested in actually calculating the correlation coefficient will use a computer program, as we do in this chapter. If you are interested in a detailed illustration of the calculations, refer to Chapter 3, in the section titled, “Describing the Relationship between Two Characterisitics,” and the study by Hébert and colleagues (1997).
Recall that the formula for the Pearson product moment correlation coefficient, symbolized by r, is
where X stands for the independent variable and Y for the outcome variable.
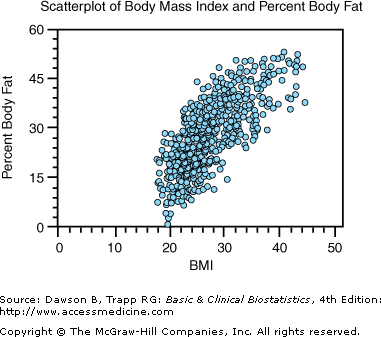
![]() A highly recommended first step in looking at the relationship between two numerical characteristics is to examine the relationship graphically. Figure 8–2 is a scatterplot of the data, with body mass index (BMI) on the X-axis and percent body fat on the Y-axis. We see from Figure 8–2 that a positive relationship exists between these two characteristics: Small values for BMI are associated with small values for percent body fat. The question of interest is whether the observed relationship is statistically significant. (A large number of duplicate or overlapping data points occur in this plot because the sample size is so large.)
A highly recommended first step in looking at the relationship between two numerical characteristics is to examine the relationship graphically. Figure 8–2 is a scatterplot of the data, with body mass index (BMI) on the X-axis and percent body fat on the Y-axis. We see from Figure 8–2 that a positive relationship exists between these two characteristics: Small values for BMI are associated with small values for percent body fat. The question of interest is whether the observed relationship is statistically significant. (A large number of duplicate or overlapping data points occur in this plot because the sample size is so large.)
Figure 8–2.
Scatterplot of body mass index and percent body fat. (Data, used with permission, from Jack son A, Stanforth PR, Gagnon J, Rankinen T, Leon AS, Rao DC, et al: The effect of sex, age and race on estimating percentage body fat from body mass index: The Heritage Family Study. Int J Obes Relat Metab Disord 2002;26:789–796. Plot produced with NCSS; used with permission.)
The extent of the relationship can be found by calculating the correlation coefficient. Using a statistical program, the correlation between BMI and percent body fat is 0.73, indicating a strong relationship between these two measures. Use the CD-ROM [available only with the book] to confirm our calculations. Also, see Chapter 3, in the section titled, “Describing the Relationship between Two Characterisitics,” for a review of the properties of the correlation coefficient.
The size of the correlation required for statistical significance is, of course, related to the sample size. With a very large sample of subjects, such as 2000, even small correlations, such as 0.06, are significant. A better way to interpret the size of the correlation is to consider what it tells us about the strength of the relationship.
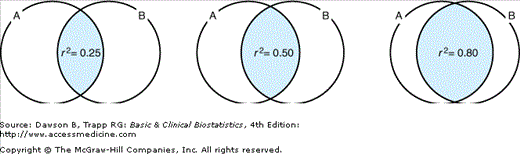
![]() The correlation coefficient can be squared to form the statistic called the coefficient of determination. For the subjects in the study by Jackson, the coefficient of determination is (0.73)2, or 0.53. This means that 53% of the variation in the values for one of the measures, such as percent body fat, may be accounted for by knowing the BMI. This concept is demonstrated by the Venn diagrams in Figure 8–3. For the left diagram, r2 = 0.25; so 25% of the variation in A is accounted for by knowing B (or vice versa). The middle diagram illustrates r2 = 0.50, similar to the value we observed, and the diagram on the right represents r2 = 0.80.
The correlation coefficient can be squared to form the statistic called the coefficient of determination. For the subjects in the study by Jackson, the coefficient of determination is (0.73)2, or 0.53. This means that 53% of the variation in the values for one of the measures, such as percent body fat, may be accounted for by knowing the BMI. This concept is demonstrated by the Venn diagrams in Figure 8–3. For the left diagram, r2 = 0.25; so 25% of the variation in A is accounted for by knowing B (or vice versa). The middle diagram illustrates r2 = 0.50, similar to the value we observed, and the diagram on the right represents r2 = 0.80.
The coefficient of determination tells us how strong the relationship really is. In the health literature, confidence limits or results of a statistical test for significance of the correlation coefficient are also commonly presented.
![]() The symbol for the correlation coefficient in the population (the population parameter) is ρ (lower case Greek letter rho). In a random sample, ρ is estimated by r. If several random samples of the same size are selected from a given population and the correlation coefficient r is calculated for each, we expect r to vary from one sample to another but to follow some sort of distribution about the population value ρ. Unfortunately, the sampling distribution of the correlation does not behave as nicely as the sampling distribution of the mean, which is normally distributed for large samples.
The symbol for the correlation coefficient in the population (the population parameter) is ρ (lower case Greek letter rho). In a random sample, ρ is estimated by r. If several random samples of the same size are selected from a given population and the correlation coefficient r is calculated for each, we expect r to vary from one sample to another but to follow some sort of distribution about the population value ρ. Unfortunately, the sampling distribution of the correlation does not behave as nicely as the sampling distribution of the mean, which is normally distributed for large samples.
Part of the problem is a ceiling effect when the correlation approaches either –1 or +1. If the value of the population parameter is, say, 0.8, the sample values can exceed 0.8 only up to 1.0, but they can be less than 0.8 all the way to –1.0. The maximum value of 1.0 acts like a ceiling, keeping the sample values from varying as much above 0.8 as below it, and the result is a skewed distribution. When the population parameter is hypothesized to be zero, however, the ceiling effects are equal, and the sample values are approximately distributed according to the t distribution, which can be used to test the hypothesis that the true value of the population parameter ?r? is equal to zero. The following mathematical expression involving the correlation coefficient, often called the t ratio, has been found to have a t distribution with n – 2 degrees of freedom:
Let us use this t ratio to test whether the observed value of r = 0.73 is sufficient evidence with 655 observations to conclude that the true population value of the correlation ρ is different from zero.
Step 1: H0: No relationship exists between BMI and percent body fat; or, the true correlation is zero: ρ = 0.
H1: A relationship does exist between BMI and percent body fat; or, the true correlation is not zero: ρ ≠ 0.
Step 2: Because the null hypothesis is a test of whether ρ is zero, the t ratio may be used when the assumptions for correlation (see the section titled, “Assumptions in Correlation”) are met.
Step 3: Let us use α = 0.01 for this example.
Step 4: The degrees of freedom are n – 2 = 655 – 2 = 653. The value of a t distribution with 653 degrees of freedom that divides the area into the central 99% and the upper and lower 1% is approximately 2.617 (using the value for 120 df in Table A–3). We therefore reject the null hypothesis of zero correlation if (the absolute value of) the observed value of t is greater than 2.617.
Step 5: The calculation is
Step 6: The observed value of the t ratio with 653 degrees of freedom is 27.29, far greater than 2.617. The null hypothesis of zero correlation is therefore rejected, and we conclude that the relationship between BMI and percent body fat is large enough to conclude that these two variables are associated.
![]() Investigators generally want to know whether ρ = 0, and this test can easily be done with computer programs. Occasionally, however, interest lies in whether the correlation is equal to a specific value other than zero. For example, consider a diagnostic test that gives accurate numerical values but is invasive and somewhat risky for the patient. If someone develops an alternative testing procedure, it is important to show that the new procedure is as accurate as the test in current use. The approach is to select a sample of patients and perform both the current test and the new procedure on each patient and then calculate the correlation coefficient between the two testing procedures.
Investigators generally want to know whether ρ = 0, and this test can easily be done with computer programs. Occasionally, however, interest lies in whether the correlation is equal to a specific value other than zero. For example, consider a diagnostic test that gives accurate numerical values but is invasive and somewhat risky for the patient. If someone develops an alternative testing procedure, it is important to show that the new procedure is as accurate as the test in current use. The approach is to select a sample of patients and perform both the current test and the new procedure on each patient and then calculate the correlation coefficient between the two testing procedures.
Either a test of hypothesis can be performed to show that the correlation is greater than a given value, or a confidence interval about the observed correlation can be calculated. In either case, we use a procedure called Fisher’s z transformation to test any null hypothesis about the correlation as well as to form confidence intervals.
To use Fisher’s exact test, we first transform the correlation and then use the standard normal (z) distribution. We need to transform the correlation because, as we mentioned earlier, the distribution of sample values of the correlation is skewed when ρ ≠ 0. Although this method is a bit complicated, it is actually more flexible than the t test, because it permits us to test any null hypothesis, not simply that the correlation is zero. Fisher’s z transformation was proposed by the same statistician (Ronald Fisher) who developed Fisher’s exact test for 2 × 2 contingency tables (discussed in Chapter 6).
Fisher’s z transformation is
where ln represents the natural logarithm. Table A–6 gives the z transformation for different values of r, so we do not actually need to use the formula. With moderate-sized samples, this transformation follows a normal distribution, and the following expression for the z test can be used:
To illustrate Fisher’s z transformation for testing the significance of ρ, we evaluate the relationship between BMI and percent body fat (Jackson et al, 2002). The observed correlation between these two measures was 0.73. Jackson and his colleagues may have expected a sizable correlation between these two measures; let us suppose they want to know whether the correlation is significantly greater than 0.65. A one-tailed test of the null hypothesis that ρ ≤ 0.65, which they hope to reject, may be carried out as follows.
Step 1: H0: The relationship between BMI and percent body fat is ≤0.65; or, the true correlation ρ ≤ 0.65.
H1: The relationship between BMI and percent body fat is >0.65; or, the true correlation ρ > 0.65.
Step 2: Fisher’s z transformation may be used with the correlation coefficient to test any hypothesis.
Step 3: Let us again use α = 0.01 for this example.
Step 4: The alternative hypothesis specifies a one-tailed test. The value of the z distribution that divides the area into the lower 99% and the upper 1% is approximately 2.326 (from Table A–2). We therefore reject the null hypothesis that the correlation is ≤ 0.65 if the observed value of z is > 2.326.
Step 5: The first step is to find the transformed values for r = 0.73 and ρ = 0.65 from Table A–6; these values are 0.929 and 0.775, respectively. Then, the calculation for the z test is
Step 6: The observed value of the z statistic, 3.93, exceeds 2.358. The null hypothesis that the correlation is 0.65 or less is rejected, and the investigators can be assured that the relationship between BMI and body fat is greater than 0.65.
A major advantage of Fisher’s z transformation is that confidence intervals can be formed. The transformed value of the correlation is used to calculate confidence limits in the usual manner, and then they are transformed back to values corresponding to the correlation coefficient.
To illustrate, we calculate a 95% confidence interval for the correlation coefficient 0.73 in Jackson and colleagues (2002). We use Fisher’s z transformation of 0.73 = 0.929 and the z distribution in Table A–2 to find the critical value for 95%. The confidence interval is
Transforming the limits 0.852 and 1.006 back to correlations using Table A–6 in reverse gives approximately r = 0.69 and r = 0.77 (using conservative values). Therefore, we are 95% confident that the true value of the correlation in the population is contained within this interval. Note that 0.65 is not in this interval, which is consistent with our conclusion that the observed correlation of 0.73 is different from 0.65.
Surprisingly, computer programs do not always contain routines for finding confidence limits for a correlation. We have included a Microsoft Excel program in the Calculations folder on the CD-ROM [available only with the book] that calculates the 95% CI for a correlation.
The assumptions needed to draw valid conclusions about the correlation coefficient are that the sample was randomly selected and the two variables, X and Y, vary together in a joint distribution that is normally distributed, called the bivariate normal distribution. Just because each variable is normally distributed when examined separately, however, does not guarantee that, jointly, they have a bivariate normal distribution. Some guidance is available: If either of the two variables is not normally distributed, Pearson’s product moment correlation coefficient is not the most appropriate method. Instead, either one or both of the variables may be transformed so that they more closely follow a normal distribution, as discussed in Chapter 5, or the Spearman rank correlation may be calculated. This topic is discussed in the section titled, “Other Measures of Correlation.”
Comparing Two Correlation Coefficients
On occasion, investigators want to know if a difference exists between two correlation coefficients. Here are two specific instances: (1) comparing the correlations between the same two variables that have been measured in two independent groups of subjects and (2) comparing two correlations that involve a variable in common in the same group of individuals. These situations are not extremely common and not always contained in statistical programs. We designed Microsoft Excel programs; see the folder “Calculations” on the CD-ROM [available only with the book].
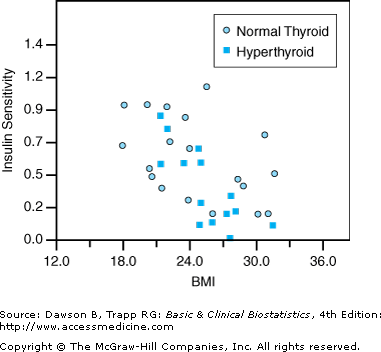
![]() Fisher’s z transformation can be used to test hypotheses or form confidence intervals about the difference between the correlations between the same two variables in two independent groups. The results of such tests are also called independent correlations. For example, Gonzalo and colleagues (1996) in Presenting Problem 4 wanted to compare the correlation between BMI and insulin sensitivity in the 14 hyperthyroid women (r = –0.775) with the correlation between BMI and insulin sensitivity in the 19 control women (r = –0.456). See Figure 8–4.
Fisher’s z transformation can be used to test hypotheses or form confidence intervals about the difference between the correlations between the same two variables in two independent groups. The results of such tests are also called independent correlations. For example, Gonzalo and colleagues (1996) in Presenting Problem 4 wanted to compare the correlation between BMI and insulin sensitivity in the 14 hyperthyroid women (r = –0.775) with the correlation between BMI and insulin sensitivity in the 19 control women (r = –0.456). See Figure 8–4.
Figure 8–4.
Scatterplot of BMI and insulin sensitivity. (Data, used with permission, from Gonzalo MA, Grant C, Moreno I, Garcia FJ, Suarez AI, Herrera-Pombo JL, et al: Glucose tolerance, insulin secretion, insulin sensitivity and glucose effectiveness in normal and overweight hyperthyroid women. Clin Endocrinol (Oxf) 1996;45:689–697. Output produced using NCSS; used with permission.)
In this situation, the value for the second group replaces z(ρ) in the numerator for the z test shown in the previous section, and l/(n – 3) is found for each group and added before taking the square root in the denominator. The test statistic is
To illustrate, the values of z from Fisher’s z transformation tables (A–6) for –0.775 and –0.456 are approximately 1.033 0.492 . (with interpolation), respectively. Note that Fisher’s z transformation is the same, regardless of whether the correlation is positive or negative. Using these values, we obtain
Assuming we choose the traditional significance level of 0.05, the value of the test statistic, 1.38, is less than the critical value, 1.96, so we do not reject the null hypothesis of equal correlations. We decide that the evidence is insufficient to conclude that the relationship between BMI and insulin sensitivity is different for hyperthyroid women from that for controls. What is a possible explanation for the lack of statistical significance? It is possible that there is no difference in the relationships between these two variables in the population. When sample sizes are small, however, as they are in this study, it is always advisable to keep in mind that the study may have low power.
![]() The second situation occurs when the research question involves correlations that contain the same variable (also called dependent correlations). For example, a very natural question for Nesselroad and colleagues (1996) was whether one of the finger devices was more highly correlated with the blood pressure cuff—considered to be the gold standard—than the other two. If so, this would be a product they might wish to recommend for patients to use at home. To illustrate, we compare the diastolic reading with device 1 and the cuff (rXY = 0.32) to the diastolic reading with device 2 and the cuff (rXZ = 0.45).
The second situation occurs when the research question involves correlations that contain the same variable (also called dependent correlations). For example, a very natural question for Nesselroad and colleagues (1996) was whether one of the finger devices was more highly correlated with the blood pressure cuff—considered to be the gold standard—than the other two. If so, this would be a product they might wish to recommend for patients to use at home. To illustrate, we compare the diastolic reading with device 1 and the cuff (rXY = 0.32) to the diastolic reading with device 2 and the cuff (rXZ = 0.45).
There are several formulas for testing the difference between two dependent correlations. We present the simplest one, developed by Hotelling (1940) and described by Glass and Stanley (1970) on pages 310–311 of their book. We will show the calculations for this example but, as always, suggest that you use a computer program. The formula follows the t distribution with n – 3 degrees of freedom; it looks rather forbidding and requires the calculation of several correlations:
We designate the cuff reading as X, device 1 as Y, and device 2 as Z. We therefore want to compare rXY with rXZ. Both correlations involve the X, or cuff, reading, so these correlations are dependent. To use the formula, we also need to calculate the correlation between device 1 and device 2, which is rYZ = 0.54. Table 8–1 shows the correlations needed for this formula.
| Pearson Correlations Section | ||||
|---|---|---|---|---|
| Cuff Diastolic | Device 1 Diastolic | Device 2 Diastolic | Device 3 Diastolic | |
| Cuff Diastolic | 1.0000 | 0.3209a | 0.4450 | 0.3592 |
| 0.0000 | 0.0011 | 0.0000 | 0.0002 | |
| 100.0000 | 100.0000 | 100.0000 | 100.0000 | |
| Device 1 Diastolic | 0.3210 | 1.0000 | 0.5364 | 0.5392 |
| 0.0011 | 0.0000 | 0.0000 | 0.0000 | |
| 100.0000 | 100.0000 | 100.0000 | 100.0000 | |
| Device 2 Diastolic | 0.4450 | 0.5364 | 1.0000 | 0.5629 |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 100.0000 | 100.0000 | 100.0000 | 100.0000 | |
| Device 3 Diastolic | 0.3592 | 0.5392 | 0.5629 | 1.0000 |
| 0.0002 | 0.0000 | 0.0000 | 0.0000 | |
| 100.0000 | 100.0000 | 100.0000 | 100.0000 | |
The calculations are
You know by now that the difference between these two correlations is not statistically significant because the observed value of t is –1.50, and |–1.50| = 1.50 is less than the critical value of t with 97 degrees of freedom, 1.99. This conclusion corresponds to that by Nesselroad and his colleagues in which they recommended that patients be cautioned that the finger blood pressure devices may not perform as marketed.
We designed a Microsoft Excel program for these calculations as well. It is included on the CD-ROM [available only with the book] in a folder called “Calculations” and is entitled “z for 2 dept r’s.”
Other Measures of Correlation
Several other measures of correlation are often found in the medical literature. Spearman’s rho, the rank correlation introduced in Chapter 3, is used with ordinal data or in situations in which the numerical variables are not normally distributed. When a research question involves one numerical and one nominal variable, a correlation called the point–biserial correlation is used. With nominal data, the risk ratio, or kappa (κ), discussed in Chapter 5, can be used.
![]() Recall that the value of the correlation coefficient is markedly influenced by extreme values and thus does not provide a good description of the relationship between two variables when their distributions are skewed or contain outlying values. For example, consider the relationships among the various finger devices and the standard cuff device for measuring blood pressure from Presenting Problem 2. To illustrate, we use the first 25 subjects from this study, listed in Table 8–2 (see the file entitled “Nesselroad25” on the CD-ROM [available only with the book]).
Recall that the value of the correlation coefficient is markedly influenced by extreme values and thus does not provide a good description of the relationship between two variables when their distributions are skewed or contain outlying values. For example, consider the relationships among the various finger devices and the standard cuff device for measuring blood pressure from Presenting Problem 2. To illustrate, we use the first 25 subjects from this study, listed in Table 8–2 (see the file entitled “Nesselroad25” on the CD-ROM [available only with the book]).
| Subject | Cuff Diastolic | Device 1 Diastolic | Device 2 Diastolic | Device 3 Diastolic |
|---|---|---|---|---|
| 1 | 80 | 58 | 51 | 38 |
| 2 | 65 | 79 | 61 | 47 |
| 3 | 70 | 66 | 61 | 50 |
| 4 | 80 | 93 | 75 | 53 |
| 5 | 60 | 75 | 76 | 54 |
| 6 | 82 | 71 | 75 | 56 |
| 7 | 70 | 58 | 60 | 58 |
| 8 | 70 | 73 | 74 | 58 |
| 9 | 60 | 72 | 67 | 59 |
| 10 | 70 | 88 | 70 | 60 |
| 11 | 48 | 70 | 88 | 60 |
| 12 | 100 | 114 | 82 | 62 |
| 13 | 70 | 74 | 56 | 64 |
| 14 | 70 | 75 | 79 | 67 |
| 15 | 70 | 89 | 62 | 69 |
| 16 | 60 | 95 | 75 | 70 |
| 17 | 80 | 87 | 89 | 72 |
| 18 | 80 | 57 | 74 | 73 |
| 19 | 90 | 69 | 90 | 73 |
| 20 | 80 | 60 | 85 | 75 |
| 21 | 70 | 72 | 75 | 77 |
| 22 | 85 | 85 | 61 | 79 |
| 23 | 100 | 102 | 99 | 89 |
| 24 | 70 | 113 | 83 | 94 |
| 25 | 90 | 127 | 108 | 99 |
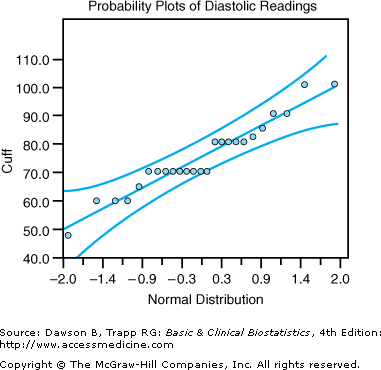
It is difficult to tell if the observations are normally distributed without looking at graphs of the data. Some statistical programs have routines to plot values against a normal distribution to help researchers decide whether a nonparametric procedure should be used. A normal probability plot for the cuff diastolic measurement is given in Figure 8–5. Use the CD-ROM [available only with the book] to produce similar plots for the finger device measurements.
When the observations are plotted on a graph, as in Figure 8–5, it appears that the data are not unduly skewed. This conclusion is consistent with the tests given for the normality of a distribution by NCSS. In the normal probability plot, if observations fall within the curved lines, the data can be assumed to be normally distributed.
As we indicated in Chapter 3, a simple method for dealing with the problem of extreme observations in correlation is to rank order the data and then recalculate the correlation on ranks to obtain the nonparametric correlation called Spearman’s rho, or rank correlation. To illustrate this procedure, we continue to use data on the first 25 subjects in the study on blood pressure devices (Presenting Problem 2), even though the distribution of the values does not require this procedure. Let us focus on the correlation between the cuff and device 2, which we learned was 0.45 in the section titled, “Comparing Correlations with Variables in Common in the Same Group.”
Table 8–3 illustrates the ranks of the diastolic readings on the first 25 subjects. Note that each variable is ranked separately; when ties occur, the average of the ranks of the tied values is used.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree