Key Concepts
 Research questions about two independent groups ask whether the means are different or the proportions are different.
Research questions about two independent groups ask whether the means are different or the proportions are different.
 Confidence intervals using the t distribution determine the confidence with which we can assume differences between two means will vary in future studies.
Confidence intervals using the t distribution determine the confidence with which we can assume differences between two means will vary in future studies.
 A pooled standard deviation is used to form the standard error of the differences.
A pooled standard deviation is used to form the standard error of the differences.
 An “eye-ball” test is helpful when reports present graphs of the mean with 95% confidence intervals.
An “eye-ball” test is helpful when reports present graphs of the mean with 95% confidence intervals.
 Using the t distribution requires the two groups to be independent from each other as well as the assumptions of normality and equal variances in the two groups.
Using the t distribution requires the two groups to be independent from each other as well as the assumptions of normality and equal variances in the two groups.
 Tests of hypothesis are another way to test the difference between two means.
Tests of hypothesis are another way to test the difference between two means.
 The assumption of equal variances can be tested with several procedures.
The assumption of equal variances can be tested with several procedures.
 The nonparametric Wilcoxon rank sum test is an excellent alternative to the t test when the assumptions of normality or equal variances are not met.
The nonparametric Wilcoxon rank sum test is an excellent alternative to the t test when the assumptions of normality or equal variances are not met.
 Both confidence intervals and statistical tests can be used to compare two proportions using the z test, again using a pooled standard deviation to form the standard error.
Both confidence intervals and statistical tests can be used to compare two proportions using the z test, again using a pooled standard deviation to form the standard error.
 The chi-square test is a very versatile statistical procedure used to test for differences in proportions as well as an association between two variables.
The chi-square test is a very versatile statistical procedure used to test for differences in proportions as well as an association between two variables.
 Fisher’s exact test is preferred to chi-square when two characteristics are being compared, each at two levels (ie, 2 × 2 tables) because it provides the exact probability.
Fisher’s exact test is preferred to chi-square when two characteristics are being compared, each at two levels (ie, 2 × 2 tables) because it provides the exact probability.
 The relative risk, or odds ratio, is appropriate if the purpose is to estimate the strength of a relationship between two nominal measures.
The relative risk, or odds ratio, is appropriate if the purpose is to estimate the strength of a relationship between two nominal measures.
 When two groups are compared on a numerical variable, the numerical variable should not be turned into categories to use the chi-square test; it is better to use the t test.
When two groups are compared on a numerical variable, the numerical variable should not be turned into categories to use the chi-square test; it is better to use the t test.
 It is possible to estimate sample sizes needed to compare the means or proportions in two groups, but it is much more efficient to use one of the statistical power packages, such as PASS in NCSS, nQuery, or SamplePower.
It is possible to estimate sample sizes needed to compare the means or proportions in two groups, but it is much more efficient to use one of the statistical power packages, such as PASS in NCSS, nQuery, or SamplePower.
Presenting Problems
Kline and colleagues (2002) published a study on the safe use of d-dimer for patients seen in the emergency department with suspected pulmonary embolism (PE). We used this study in Chapter 3 to illustrate descriptive measures and graphs useful with numeric data. In this chapter we continue our analysis of some of the information collected by Kline and colleagues. We will illustrate the t test for two independent samples and learn whether there was a significant difference in pulse oximetry in patients who did and those who did not have a PE. The entire data set is in a folder on the CD-ROM [available only with the book] entitled “Kline.”
Cryosurgery is commonly used for treatment of cervical intraepithelial neoplasia (CIN). The procedure is associated with pain and uterine cramping. Symptoms are mediated by the release of prostaglandins and endoperoxides during the thermodestruction of the cervical tissue. The most effective cryosurgical procedure, the so-called 5-min double freeze, produces significantly more pain and cramping than other cryosurgical methods. It is important to make this procedure as tolerable as possible.
A study to compare the perceptions of both pain and cramping in women undergoing the procedure with and without a paracervical block was undertaken by Harper (1997). All participants received naproxen sodium 550 mg prior to surgery. Those receiving the paracervical block were injected with 1% lidocaine with epinephrine at 9 and 3 o’clock at the cervicovaginal junction to infiltrate the paracervical branches of the uterosacral nerve.
Within 10 min of completing the cryosurgical procedure, the intensity of pain and cramping were assessed on a 100-mm visual analog scale (VAS), in which 0 represented no pain or cramping and 100 represented the most severe pain and cramping. Patients were enrolled in a nonrandom fashion (the first 40 women were treated without anesthetic and the next 45 with a paracervical block), and there was no placebo treatment.
We use data on intensity of cramping and pain to illustrate the t test for comparing two groups and the nonparametric Wilcoxon rank sum test. The investigator also wanted to compare the proportion of women who had no pain or cramping at the first and second freezes. We use these observations to illustrate the chi-square test. Data from the study are given in the sections titled, “Comparing Means in Two Groups with the t Test” and “Using Chi-Square Tests” and on the CD-ROM [available only with the book].
In Chapter 3, we briefly looked at the results from a survey to assess domestic violence (DV) education and training and the use of DV screening among pediatricians and family physicians (Lapidus et al, 2002). The survey asked physicians questions about any training they may have had, their use in screening, and their own personal history of DV. Domestic violence was defined as “past or current physical, sexual, emotional or verbal harm to a woman caused by a spouse, partner or family member.” Please see Chapter 3 for more detail. We use the data to illustrate confidence intervals for proportions. Data are given in the section titled, “Decisions About Proportions in Two Independent Groups” and on the CD-ROM [available only with the book].
Purpose of the Chapter
In the previous chapter, we looked at statistical methods to use when the research question involves:
- 1. A single group of subjects and the goal is to compare a proportion or mean to a norm or standard.
- 2. A single group measured twice and the goal is to estimate how much the proportion or mean changes between measurements.
![]() The procedures in this chapter are used to examine differences between two independent groups (when knowledge of the observations for one group does not provide any information about the observations in the second group). In all instances, we assume the groups represent random samples from the larger population to which researchers want to apply the conclusions.
The procedures in this chapter are used to examine differences between two independent groups (when knowledge of the observations for one group does not provide any information about the observations in the second group). In all instances, we assume the groups represent random samples from the larger population to which researchers want to apply the conclusions.
When the research question asks whether the means of two groups are equal (numerical observations), we can use either the two-sample (independent-groups) t test or the Wilcoxon rank sum test. When the research question asks whether proportions in two independent groups are equal, we can use several methods: the z distribution to form a confidence interval and the z distribution, chi-square, or Fisher’s exact test to test hypotheses.
Decisions About Means in Two Independent Groups
Investigators often want to know if the means are equal or if one mean is larger than the other mean. For example, Kline and colleagues (2002) in Presenting Problem 1 wanted to know if information on a patient’s status in the emergency department can help indicate risk for PE. We noted in Chapter 5 that the z test can be used to analyze questions involving means if the population standard deviation is known. This, however, is rarely the case in applied research, and researchers typically use the t test to analyze research questions involving two independent means.
Surveys of statistical methods used in the medical literature consistently indicate that t tests and chi-square tests are among the most commonly used. Furthermore, Williams and coworkers (1997) noted a number of problems in using the t test, including no discussion of assumptions, in more than 85% of the articles. Welch and Gabbe (1996) noted errors in using the t test when a nonparametric procedure is called for and in using the chi-square test when Fisher’s exact test should be employed. Thus, being able to evaluate the use of tests comparing means and proportions—whether they are used properly and how to interpret the results—is an important skill for medical practitioners.
![]() The means and standard deviations from selected variables from the Kline study are given in Table 6–1. In this chapter, we analyze the pulse oximetry data for patients who had a PE and those who did not. We want to know the average difference in pulse oximetry for these two groups of patients. Pulse oximetry is a numerical variable, and we know that means provide an appropriate way to describe the average with numerical variables. We can find the mean pulse oximetry for each set of patients and form a confidence interval for the difference.
The means and standard deviations from selected variables from the Kline study are given in Table 6–1. In this chapter, we analyze the pulse oximetry data for patients who had a PE and those who did not. We want to know the average difference in pulse oximetry for these two groups of patients. Pulse oximetry is a numerical variable, and we know that means provide an appropriate way to describe the average with numerical variables. We can find the mean pulse oximetry for each set of patients and form a confidence interval for the difference.
| Variable | PE Positive n/mean ± SD | PE Negative n/mean ± SD | Difference |
|---|---|---|---|
| Age, years ± SD | 181/56.2 ± 17.7 | 750/48.7 ± 18.1 | 7 (4.1, 9.9) |
| Respiratory rate (breaths/min) | 170/21.7 ± 6.7 | 699/20.6 ± 6.7 | 1 (–0.1, 2.1) |
| Heart rate (beats/min) | 180/96.1 ± 20.4 | 750/91.5 ± 20.5 | 4 (1.6, 8.4) |
| Systolic blood pressure (mm Hg) | 181/134.0 ± 23.4 | 748/139.3 ± 26.6 | –5 (–9.3, –0.7) |
| Shock index (HR/SBP) | 181/0.741 ± 0.214 | 750/0.6809 ± 0.200 | 0.05 (0.01, 0.09) |
| Pulse oximetry (%, room air) | 181/93.4 ± 5.9 | 740/95.8 ± 4.0 | –3 (–3.7, –2.3) |
| pH | 98/7.44 ± 0.05 | 320/7.42 ± 0.10 | 0.02 (0.005, 0.04) |
| Pco2 | 158/35.4 ± 5.4 | 635/36.9 ± 6.8 | –1 (–2.1, 0.2) |
The form for a confidence interval for the difference between two means is
If we use symbols to illustrate a confidence interval for the difference between two means and let 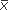 1 stand for the mean of the first group and
1 stand for the mean of the first group and 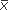 2 for the mean of the second group, then we can write the difference between the two means as
2 for the mean of the second group, then we can write the difference between the two means as 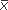 1 –
1 – 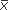 2.
2.
As you know from the previous chapter, the number related to the level of confidence is the critical value from the t distribution. For two means, we use the t distribution with (n1 – 1) degrees of freedom corresponding to the number of subjects in group 1, plus (n2 – 1) degrees of freedom corresponding to the number of subjects in group 2, for a total of (n1 + n2 – 2) degrees of freedom.
![]() With two groups, we also have two standard deviations. One assumption for the t test, however, is that the standard deviations are equal (the section titled, “Assumptions for the t Distribution”). We achieve a more stable estimate of the true standard deviation in the population if we average the two separate standard deviations to obtain a pooled standard deviation based on a larger sample size. The pooled standard deviation is a weighted average of the two variances (squared standard deviations) with weights based on the sample sizes. Once we have the pooled standard deviation, we use it in the formula for the standard error of the difference between two means, the last term in the preceding equation for a confidence interval.
With two groups, we also have two standard deviations. One assumption for the t test, however, is that the standard deviations are equal (the section titled, “Assumptions for the t Distribution”). We achieve a more stable estimate of the true standard deviation in the population if we average the two separate standard deviations to obtain a pooled standard deviation based on a larger sample size. The pooled standard deviation is a weighted average of the two variances (squared standard deviations) with weights based on the sample sizes. Once we have the pooled standard deviation, we use it in the formula for the standard error of the difference between two means, the last term in the preceding equation for a confidence interval.
The standard error of the mean difference tells us how much we can expect the differences between two means to vary if a study is repeated many times. First we discuss the logic behind the standard error and then we illustrate its use with data from the study by Kline and colleagues (2002).
The formula for the pooled standard deviation looks complicated, but remember that the calculations are for illustration only, and we generally use a computer to do the computation. We first square the standard deviation in each group (SD1 and SD2) to obtain the variance, multiply each variance by the number in that group minus 1, and add to get (n1 – 1) SD12 + (n2 – 1) SD22. The standard deviations are based on the samples because we do not know the true population standard deviations. Next we divide by the sum of the number of subjects in each group minus 2.
Finally, we take the square root to find the pooled standard deviation.
The pooled standard deviation is used to calculate the standard error of the difference. In words, the standard error of the difference between two means is the pooled standard deviation, SDp, multiplied by the square root of the sum of the reciprocals of the sample sizes. In symbols, the standard error of the mean difference is
Based on the study by Kline and colleagues (2002), a PE was positive in 181 patients and negative in 740 patients (see Table 6–1). Substituting 181 and 740 for the two sample sizes and 5.9 4.0 . for the two standard deviations, we have
Does it make sense that the value of the pooled standard deviation is always between the two sample standard deviations? In fact, if the sample sizes are equal, it is the mean of the two standard deviations (see Exercise 4).
Finally, to find the standard error of the difference, we substitute 4.4 for the pooled standard deviation and 181 and 740 for the sample sizes and obtain
The standard error of the difference in pulse oximetry measured in the two groups is 0.37. The standard error is simply the standard deviation of the differences in means if we repeated the study many times. It indicates that we can expect the mean differences in a large number of similar studies to have a standard deviation of about 0.37.
Now we have all the information needed to find a confidence interval for the mean difference in pulse oximetry. From Table 6–1, the mean pulse oximetry levels were 95.8 for patients not having a PE and 93.4 for patients with a PE. To find the 95% confidence limits for the difference between these means (95.8 – 93.4 = 2.4), we use the two-tailed value from the t distribution for 181 + 740 – 2 = 919 degrees of freedom (Table A–3) that separates the central 95% of the t distribution from the 5% in the tails. The value is 1.96; note that the value z is also 1.96, demonstrating once more that the t distribution approaches the shape of the z distribution with large samples.
Using these numbers in the formula for 95% confidence limits, we have 2.4 ± (1.96) (0.37) = 2.4 ± 0.73, or 1.67 to 3.13. Interpreting this confidence interval, we can be 95% confident that the interval from 1.67 to 3.13 contains the true mean difference in pulse oximetry.a Because the interval does not contains the value 0, it is not likely that the mean difference is 0. Table 6–2 illustrates the NCSS procedure for comparing two means and determining a confidence interval (see the bold line). The confidence interval found by NCSS is 1.66 to 3.11, slightly different from ours due to rounding. Use the data set on the CD-ROM [available only with the book] in the Kline folder and replicate this analysis.
aTo be precise, the confidence interval is interpreted as follows: 95% of such confidence intervals contain the true difference between the two means if repeated random samples of operating room times are selected and 95% confidence intervals are calculated for each sample.
| Two-Sample Test Report | ||||||
|---|---|---|---|---|---|---|
| Variable | Pulse Oximetry | |||||
| Descriptive Statistics Section | ||||||
| Variable | Count | Mean | Standard Deviation | Standard Error | 95% LCL of Mean | 95% UCL of Mean |
| PE negative | 742 | 95.76685 | 3.993021 | 0.1465884 | 95.47954 | 96.05415 |
| PE positive | 181 | 93.38122 | 5.95758 | 0.4428234 | 92.50742 | 94.255 |
| Confidence-Limits of Difference Section | ||||||
| Variance Assumption | DF | Mean Difference | Standard Deviation | Standard Error | 95% LCL of Mean | 95% UCL of Mean |
| Equal | 921 | 2.385631 | 4.44576 | 0.3685578 | 1.663271 | 3.107991 |
| Unequal | 220.97 | 2.385631 | 7.171957 | 0.4664555 | 1.471395 | 3.299867 |
| Note: T-alpha (Equal) = 1.9600, T-alpha (Unequal) = 1.9600 | ||||||
Recall in Chapter 3, we used box plots to examine the distribution of shock index for those with and without PE (Figure 3–6). Do you think the difference is statistically significant? Use the data disk [available only with the book] and the independent groups t test. NCSS gives the 95% confidence interval as –9.375404E-02 to –0.0280059. Recall that in scientific notation, we move the decimal as many digits to the left as indicated following “E,” so the interval is –0.09375404 to –0.0280059, or about –0.094 to –0.028. What can we conclude about the difference in shock index?
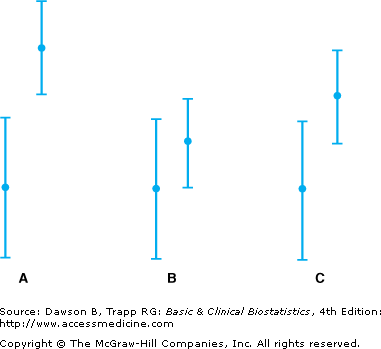
![]() Readers of the literature and those attending presentations of research findings find it helpful if information is presented in graphs and tables, and most researchers use them whenever possible. We introduced error bar plots in Chapter 3 when we talked about different graphs that can be used to display data for two or more groups, and error bar plots can be used for an “eyeball” test of the mean in two (or more) groups. Using error bar charts with 95% confidence limits, one of the following three results always occurs:
Readers of the literature and those attending presentations of research findings find it helpful if information is presented in graphs and tables, and most researchers use them whenever possible. We introduced error bar plots in Chapter 3 when we talked about different graphs that can be used to display data for two or more groups, and error bar plots can be used for an “eyeball” test of the mean in two (or more) groups. Using error bar charts with 95% confidence limits, one of the following three results always occurs:
- 1. The top of one error bar does not overlap with the bottom of the other error bar, as illustrated in Figure 6–1A. When this occurs, we can be 95% sure that the means in two groups are significantly different.
- 2. The top of one 95% error bar overlaps the bottom of the other so much that the mean value for one group is contained within the limits for the other group (see Figure 6–1B). This indicates that the two means are not statistically significant.
- 3. If 95% error bars overlap some but not as much as in situation 2, as in Figure 6–1C, we do not know if the difference is significant unless we form a confidence interval or do a statistical test for the difference between the two means.
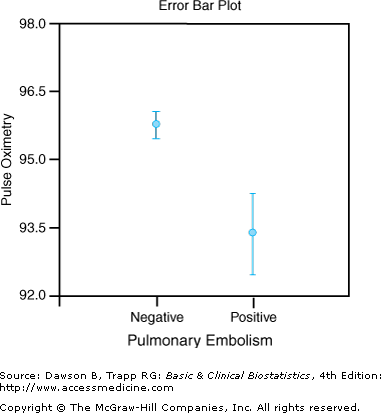
To use the eyeball method for the mean pulse oximetry, we find the 95% confidence interval for the mean in each individual group. We can refer to Table 6–2 where NCSS reports the confidence interval for the mean in each group in the Descriptive Statistics Section. The 95% confidence interval for pulse oximetry in patients without a PE is 95.5 to 96.1 92.5 . to 94.3 in patients with a PE.
These two confidence intervals are shown in Figure 6–2. This example illustrates the situation in Figure 6–1A: The graphs do not overlap, so we can conclude that mean pulse oximetry in the two groups is different.
Figure 6–2.
Illustration of error bars. (Data, used with permission of the authors and publisher, Kline JA, Nelson RD, Jackson RE, Courtney DM: Criteria for the safe use of d-dimer testing in emergency department patients with suspected pulmonary embolism: A multicenter US study. Ann Emergency Med 2002;39:144–152. Plot produced with NCSS; used with permission.)
A word of caution is needed. When the sample size in each group is greater than ten, the 95% confidence intervals are approximately equal to the mean ±2 standard errors (SE), so graphs of the mean ±2 standard errors can be used for the eyeball test. Some authors, however, instead of using the mean ±2 standard errors, present a graph of the mean ±1 standard error or the mean ±2 standard deviations (SD). Plus or minus one standard error gives only a 68% confidence interval for the mean. Plus or minus 2 standard deviations results in the 95% interval in which the individual measurements are found if the observations are normally distributed. Although nothing is inherently wrong with these graphs, they cannot be interpreted as indicating differences between means. Readers need to check graph legends very carefully before using the eyeball test to interpret published graphs.
![]() Three assumptions are needed to use the t distribution for either determining confidence intervals or testing hypotheses. We briefly mention them here and outline some options to use if observations do not meet the assumptions.
Three assumptions are needed to use the t distribution for either determining confidence intervals or testing hypotheses. We briefly mention them here and outline some options to use if observations do not meet the assumptions.
- 1. As is true with one group, the t test assumes that the observations in each group follow a normal distribution. Violating the assumption of normality gives P values that are lower than they should be, making it easier to reject the null hypothesis and conclude a difference when none really exists. At the same time, confidence intervals are narrower than they should be, so conclusions based on them may be wrong. What is the solution to the problem? Fortunately, this issue is of less concern if the sample sizes are at least 30 in each group. With smaller samples that are not normally distributed, a nonparametric procedure called the Wilcoxon rank sum test is a better choice (see the section titled, “Comparing Means with the Wilcoxon Rank Sum Test”).
- 2. The standard deviations (or variances) in the two samples are assumed to be equal (statisticians call them homogeneous variances). Equal variances are assumed because the null hypothesis states that the two means are equal, which is actually another way of saying that the observations in the two groups are from the same population. In the population from which they are hypothesized to come, there is only one standard deviation; therefore, the standard deviations in the two groups must be equal if the null hypothesis is true. What is the solution when the standard deviations are not equal? Fortunately, this assumption can be ignored when the sample sizes are equal (Box, 1953). This is one of several reasons many researchers try to have fairly equal numbers in each group. (Statisticians say the t test is robust with equal sample sizes.) Statistical tests can be used to decide whether standard deviations are equal before doing a t test (see the section titled, “Comparing Variation in Independent Groups”).
- 3. The final assumption is one of independence, meaning that knowing the values of the observations in one group tells us nothing about the observations in the other group. In contrast, consider the paired group design discussed in Chapter 5, in which knowledge of the value of an observation at the time of the first measurement does tell us something about the value at the time of the second measurement. For example, we would expect a subject who has a relatively low value at the first measurement to have a relatively low second measurement as well. For that reason, the paired t test is sometimes referred to as the dependent groups t test. No statistical test can determine whether independence has been violated, however, so the best way to ensure two groups are independent is to design and carry out the study properly.
![]() In the study on uterine cryosurgery, Harper (1997) wanted to compare the severity of pain and cramping perceived by women undergoing the usual practice of cryosurgery with that of women who received a paracervical block prior to the cryosurgery. She used a visual analog scale from 0 to 100 to represent the amount of pain or cramping, with higher scores indicating more pain or cramping. Means and standard deviations for various pain and cramping scores are reported in Table 6–3.
In the study on uterine cryosurgery, Harper (1997) wanted to compare the severity of pain and cramping perceived by women undergoing the usual practice of cryosurgery with that of women who received a paracervical block prior to the cryosurgery. She used a visual analog scale from 0 to 100 to represent the amount of pain or cramping, with higher scores indicating more pain or cramping. Means and standard deviations for various pain and cramping scores are reported in Table 6–3.
| Variable | Group | N | Mean | Standard Deviation | Standard Error of Mean |
|---|---|---|---|---|---|
| First cramping score | No block | 39 | 48.51 | 28.04 | 4.49 |
| Block | 45 | 32.88 | 25.09 | 3.74 | |
| First pain score | No block | 39 | 38.82 | 28.69 | 4.59 |
| Block | 45 | 33.33 | 29.77 | 4.44 | |
| Second cramping score | No block | 39 | 32.10 | 28.09 | 4.50 |
| Block | 45 | 25.60 | 27.86 | 4.15 | |
| Second pain score | No block | 39 | 23.77 | 26.14 | 4.19 |
| Block | 45 | 25.33 | 27.27 | 4.07 | |
| Total cramping score | No block | 39 | 51.41 | 28.11 | 4.50 |
| Block | 45 | 35.60 | 28.45 | 4.24 | |
| Total pain score | No block | 39 | 43.49 | 29.06 | 4.65 |
| Block | 45 | 38.58 | 27.74 | 4.14 |
The research question is whether women who received a paracervical block prior to the cryosurgery had less severe total cramping than women who did not have a paracervical block. Stating the research question in this way implies that the researcher is interested in a directional or one-tailed test, testing only whether the severity of cramping is less in the group with a paracervical block. From Table 6–3, the mean total cramping score is 35.60 on a scale from 0 to 100 for women who had the paracervical block versus 51.41 for women who did not. This difference could occur by chance, however, and we need to know the probability that a difference this large would occur by chance before we can conclude that these results can generalize to similar populations of women.
The sample sizes are larger than 30 and are fairly similar, so the issues of normality and equal variances are of less concern, and the t test for two independent groups can be used to answer this question. Let us designate women with a paracervical block as group 1 and those without a paracervical block as group 2. The six steps in testing the hypothesis are as follows:
Step 1: H0: Women who had a paracervical block prior to cryosurgery had a mean cramping score at least as high as women who had no block. In symbols, we express it as
H1: Women who had a paracervical block prior to cryosurgery had a lower mean cramping score than women who had no block. In symbols, we express it as
Step 2: The t test can be used for this research question (assuming the observations follow a normal distribution, the standard deviations in the population are equal, and the observations are independent). The t statistic for testing the mean difference in two independent groups has the difference between the means in the numerator and the standard error of the mean difference in the denominator; in symbols it is
where there are (n1 – 1) + (n2 – 1) = (n1 + n2 – 2) degrees of freedom and SDp is the pooled standard deviation. (See section titled, “Comparing Two Means Using Confidence Intervals” for details on how to calculate SDp.)
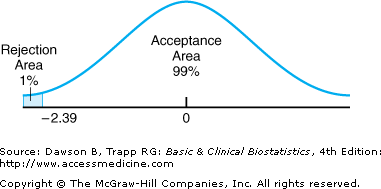
Step 3: Let us use α = 0.01 so there will be only 1 chance in 100 that we will incorrectly conclude that cramping is less with cryotherapy if it really is not.
Step 4: The degrees of freedom are (n1 + n2 – 2) = 45 + 39 – 2 = 82. For a one-tailed test, the critical value separating the lower 1% of the t distribution from the upper 99% is approximately –2.39 (using the more conservative value for 60 degrees of freedom in Table A–3). So, the decision is to reject the null hypothesis if the observed value of t is less than –2.39 (Figure 6–3).
Step 5: The calculations for the t statistic follow. First, the pooled standard deviation is 28.27 (see Exercise 2). Then the observed value for t is
Please check our calculations using the CD-ROM [available only with the book] and the data set in the Harper folder.
Step 6: The observed value of t, –2.56, is less than the critical value of –2.39, so we reject the null hypothesis. In plain words, there is enough evidence in this study to conclude that, on the average, women who had a paracervical block prior to cryosurgery experienced less total cramping than women who did not have the block. Note that our conclusion refers to women on the average and does not mean that every woman with a paracervical block would experience less cramping.
The t test for independent groups assumes equal standard deviations or variances, called homogeneous variances, as do the analysis of varianceprocedures to compare more than two groups discussed in Chapter 7. We can ignore this assumption if the sample sizes are approximately equal. If not, many statisticians recommend testing to see if the standard deviations are equal. If they are not equal, the degrees of freedom for the t test can be adjusted downward, making it more difficult to reject the null hypothesis; otherwise, a nonparametric method, such as the Wilcoxon rank sum test (illustrated in the next section), can be used.
![]() A common statistical test for the equality of two variances is called the F test. This test can be used to determine if two standard deviations are equal, because the standard deviation is the square root of the variance, and if the variances are equal, so are the standard deviations. Many computer programs calculate the F test. This test has some major shortcomings, as we discuss later on; however, an illustration is worthwhile because the F test is the statistic used to compare more than two groups (analysis of variance, the topic of Chapter 7).
A common statistical test for the equality of two variances is called the F test. This test can be used to determine if two standard deviations are equal, because the standard deviation is the square root of the variance, and if the variances are equal, so are the standard deviations. Many computer programs calculate the F test. This test has some major shortcomings, as we discuss later on; however, an illustration is worthwhile because the F test is the statistic used to compare more than two groups (analysis of variance, the topic of Chapter 7).
To calculate the F test, the larger variance is divided by the smaller variance to obtain a ratio, and this ratio is then compared with the critical value from the F distribution (corresponding to the desired significance level). If two variances are about equal, their ratio will be about 1. If their ratio is significantly greater than 1, we conclude the variances are unequal. Note that we guaranteed the ratio is at least 1 by putting the larger variance in the numerator. How much greater than 1 does F need to be to conclude that the variances are unequal? As you might expect, the significance of F depends partly on the sample sizes, as is true with most statistical tests.
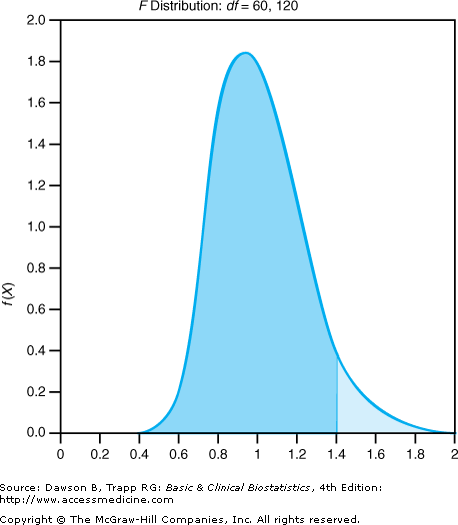
Sometimes common sense indicates no test of homogeneous variances is needed. For example, the standard deviations of the total cramping scores in the study by Harper are approximately 28.1 and 28.5, so the variances are 789.6 and 812.3. The practical significance of this difference is nil, so a statistical test for equal variances is unnecessary, and the t test is an appropriate choice. As another example, consider the standard deviations of pH from the study by Kline and colleagues (2002) given in Table 6–1: 0.05 for the group with a PE and 0.10 for the group without a PE. The relative difference is such that a statistical test will be helpful in deciding the best approach to analysis. The null hypothesis for the test of equal variances is that the variances are equal. Using the pH variances to illustrate the F test, 0.102 = 0.01 0.05 . 2 = 0.0025, and the F ratio is (putting the larger value in the numerator) 0.01/0.0025 = 4.
Although this ratio is greater than 1, you know by now that we must ask whether a value this large could happen by chance, assuming the variances are equal. The F distribution has two values for degrees of freedom (df): one for the numerator and one for the denominator, each equal to the sample size minus 1. The F distribution for our example has 98 – 1 = 97 df for the numerator and 320 – 1 = 319 df for the denominator. Using α = 0.05, the critical value of the F distribution from Table A–4 is approximately 1.43. (Because of limitations of the table, we used 60 df for the numerator and 120 df for the denominator, resulting in a conservative value.) Because the result of the F test is 4.00, greater than 1.43, we reject the null hypothesis of equal variances. Figure 6–4 shows a graph of the F distribution to illustrate this hypothesis test.
If the F test is significant and the hypothesis of equal variances is rejected, the standard deviations from the two samples cannot be pooled for the t test because pooling assumes they are equal. When this happens, one approach is to use separate variances and decrease the degrees of freedom for the t test. Reducing the degrees of freedom requires a larger observed value for t
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree