Key Concepts
 Three factors help determine whether an observed estimate, such as the mean, is different from a norm: the size of the difference, the degree of variability, and the sample size.
Three factors help determine whether an observed estimate, such as the mean, is different from a norm: the size of the difference, the degree of variability, and the sample size.
 The t distribution is similar to the z distribution, especially as sample sizes exceed 30, and t is generally used in medicine when asking questions about means.
The t distribution is similar to the z distribution, especially as sample sizes exceed 30, and t is generally used in medicine when asking questions about means.
 Confidence intervals are common in the literature; they are used to determine the confidence with which we can assume future estimates (such as the mean) will vary in future studies.
Confidence intervals are common in the literature; they are used to determine the confidence with which we can assume future estimates (such as the mean) will vary in future studies.
 The logic behind statistical hypothesis tests is somewhat backwards, generally assuming there is no difference and hoping to show that a difference exists.
The logic behind statistical hypothesis tests is somewhat backwards, generally assuming there is no difference and hoping to show that a difference exists.
 Several assumptions are required to use the t distribution for confidence intervals or hypothesis tests.
Several assumptions are required to use the t distribution for confidence intervals or hypothesis tests.
 Tests of hypothesis are another way to approach statistical inference; a somewhat rigid approach with six steps is recommended.
Tests of hypothesis are another way to approach statistical inference; a somewhat rigid approach with six steps is recommended.
 Confidence intervals and statistical tests lead to the same conclusions, but confidence intervals actually provide more information and are being increasingly recommended as the best way to present results.
Confidence intervals and statistical tests lead to the same conclusions, but confidence intervals actually provide more information and are being increasingly recommended as the best way to present results.
 In hypothesis testing, we err if we conclude there is a difference when none exists (type I, or α, error), as well as when we conclude there is not difference when one does exists (type II, or β, error).
In hypothesis testing, we err if we conclude there is a difference when none exists (type I, or α, error), as well as when we conclude there is not difference when one does exists (type II, or β, error).
 Power is the complement of a type II, or β, error: it is concluding there is a difference when one does exist. Power depends on several factors, including the sample size. It is truly a key concept in statistics because it is critical that researchers have a large enough sample to detect a difference if one exists.
Power is the complement of a type II, or β, error: it is concluding there is a difference when one does exist. Power depends on several factors, including the sample size. It is truly a key concept in statistics because it is critical that researchers have a large enough sample to detect a difference if one exists.
 The P value first assumes that the null hypothesis is true and then indicates the probability of obtaining a result as or more extreme than the one observed. In more straightforward language, the P value is the probability that the observed result occurred by chance alone.
The P value first assumes that the null hypothesis is true and then indicates the probability of obtaining a result as or more extreme than the one observed. In more straightforward language, the P value is the probability that the observed result occurred by chance alone.
 The z distribution, sometimes called the z approximation to the binomial, is used to form confidence intervals and test hypotheses about a proportion.
The z distribution, sometimes called the z approximation to the binomial, is used to form confidence intervals and test hypotheses about a proportion.
 The width of confidence intervals (CI) depends on the confidence value. 99% CI are wider than 95% CI because 99% CI provide greater confidence.
The width of confidence intervals (CI) depends on the confidence value. 99% CI are wider than 95% CI because 99% CI provide greater confidence.
 Paired, or before-and-after, studies are very useful for detecting changes that might otherwise be obscured by variation within subjects, because each subject is his or her own control.
Paired, or before-and-after, studies are very useful for detecting changes that might otherwise be obscured by variation within subjects, because each subject is his or her own control.
 Paired studies are analyzed by evaluating the differences themselves. For numerical variables, the paired t test is appropriate.
Paired studies are analyzed by evaluating the differences themselves. For numerical variables, the paired t test is appropriate.
 The kappa κ statistic is used to compare the agreement between two independent judges or methods when observations are being categorized.
The kappa κ statistic is used to compare the agreement between two independent judges or methods when observations are being categorized.
 The McNemar test is the counterpart to the paired t test when observations are nominal instead of numerical.
The McNemar test is the counterpart to the paired t test when observations are nominal instead of numerical.
 The sign test can be used to test medians (instead of means) if the distribution of observations is skewed.
The sign test can be used to test medians (instead of means) if the distribution of observations is skewed.
 The Wilcoxon signed rank test is an excellent alternative to the paired t test if the observations are not normally distributed.
The Wilcoxon signed rank test is an excellent alternative to the paired t test if the observations are not normally distributed.
 To estimate the needed sample size for a study, we need to specify the level of significance (often 0.05), the desired level of power (generally 80%), the size of the difference in order to be of clinical importance, and an estimate of the standard deviation.
To estimate the needed sample size for a study, we need to specify the level of significance (often 0.05), the desired level of power (generally 80%), the size of the difference in order to be of clinical importance, and an estimate of the standard deviation.
 It is possible to estimate sample sizes needed, but it is much more efficient to use one of the statistical power packages, such as PASS in NCSS, nQuery, or SamplePower.
It is possible to estimate sample sizes needed, but it is much more efficient to use one of the statistical power packages, such as PASS in NCSS, nQuery, or SamplePower.
Presenting Problems
Barbara Dennison and her colleagues (1997) asked an intriguing question relating to nutrition in young children: How does fruit juice consumption affect growth parameters during early childhood? The American Academy of Pediatrics has warned that excessive use of fruit juice may cause gastrointestinal symptoms, including diarrhea, abdominal pain, and bloating caused by fructose malabsorption and the presence of the nonabsorbable sugar alcohol, sorbitol. Excessive fruit juice consumption has been reported as a contributing factor in failure to thrive.
These investigators designed a cross-sectional study including 116 two-year-old children and 107 five-year-old children selected from a primary care, pediatric practice. The children’s parents completed a 7-day dietary record that included the child’s daily consumption of beverage—milk, fruit juice, soda pop, and other drinks. Height was measured to the nearest 0.l cm and weight to the nearest 0.25 lb. Excess fruit juice consumption was defined as ≥ 12 fl oz/day. Both the body mass index (BMI) and the ponderal index were used as measures of obesity.
They found that the dietary energy intake of the children in their study population, 1245 kcal for the 2-year-olds and 1549 kcal for the 5-year-olds, was remarkably similar to that reported in the National Health and Nutrition Examination Survey (NHANES) taken from a nationally representative sample of white children. The prevalence of short stature and obesity was higher among children consuming excess fruit juice. Forty-two percent of children drinking ≥ 12 fl oz/day of fruit juice were short compared with 14% of children drinking < 12 fl oz/day. For obesity the percentages were 53% and 32%, respectively.
We use the observations on the group of 2-year-old children (see section titled, “Introduction to Questions About Means”), and find that the t distribution and t test are appropriate statistical approaches. The entire data set, including information on 5-year-olds as well, is available in the folder entitled “Dennison” on the CD-ROM [available only with the book].
Concerns related to the use of smallpox virus as a potential biological warfare agent have led to intense interest in evaluating the availability and safety of smallpox vaccine. Currently, the supply of smallpox vaccine is insufficient to vaccinate all United States residents.
The National Institute of Allergy and Infectious Diseases conducted a randomized, single-blind trial to determine the rate of success of inoculation with different dilutions of smallpox vaccine (Frey et al, 2002). A total of 680 healthy adult volunteers 18–32 years of age were randomly assigned to receive undiluted vaccine, a 1:5 dilution of vaccine, or a 1:10 dilution of vaccine. A primary end point of the study was the rate of success of vaccination defined by the presence of a primary vesicle at the inoculation site 7–9 days after inoculation. If no vesicle formed, revaccination with the same dilution of vaccine was administered. The investigators also wished to determine the range and frequency of adverse reactions to the vaccine. We use data from this study to illustrate statistical methods for a proportion.
Following cholecystectomy, symptoms of abdominal pain, flatulence, or dyspepsia occur frequently and are part of the “postcholecystectomy syndrome.” Postcholecystectomy diarrhea (PCD) is a well-known complication of the surgery, although the frequency of its occurrence varies considerably in clinical reports. Sauter and colleagues (2002) prospectively evaluated the frequency of PCD and changes in bowel habits in patients undergoing cholecystectomy. They also evaluated the role of bile acid malabsorption in PCD.
Fifty-one patients undergoing cholecystectomy were evaluated before, 1 month after, and 3 months after cholecystectomy. Patients were interviewed about the quality and frequency of their stools. In addition, to evaluate the role of bile acid malabsorption, serum concentrations of 7α-hydroxy-4-cholesten-3-one (7α-HCO) were measured before and after surgery.
After cholecystectomy, there was an increase in the number of patients reporting more than one bowel movement per day: 22% before surgery, 51% at 1 month, and 45% at 3 months. Those reporting loose stools also increased.
The section titled, “Confidence Intervals for the Mean Difference in Paired Designs” gives 7α-HCO levels at baseline, 1 month after surgery, and 3 months after surgery; and the data sets are in a folder on the CD-ROM [available only with the book] called “Sauter.” We use the data from this study to illustrate before and after study designs with both binary and numerical variables.
Large-vessel atherothromboembolism is a major cause of ischemic stroke. Histologic studies of atherosclerotic plaques suggest that the lesions containing a large lipid-rich necrotic core or intraplaque hemorrhage place patients at greater risk of ischemic stroke. Yuan and colleagues (2001) used high-resolution magnetic resonance imaging (MRI) to study characteristics of diseased carotid arteries to determine which plaque features might pose higher risk for future ischemic complications.
They evaluated 18 consecutive patients scheduled for carotid endarterectomy with a carotid artery MRI examination and correlated these findings with histopathologic characteristics of the surgical carotid artery specimens. The histology slides were evaluated by a pathologist who was blinded to the imaging results. It is important to establish the level of agreement between the MRI findings and histology, and we will use the observations to illustrate a measure of agreement called Cohen’s kappa κ. See the data in the section titled, “Measuring Agreement Between Two People or Methods” and the file entitled “Yuan” on the CD-ROM [available only with the book].
Purpose of the Chapter
The methods in Chapter 3 are often called descriptive statistics because they help investigators describe and summarize data. Chapter 4 provided the basic probability concepts needed to evaluate data using statistical methods. Without probability theory, we could not make statements about populations without studying everyone in the population—clearly an undesirable and often impossible task. In this chapter we begin the study of inferential statistics; these are the statistical methods used to draw conclusions from a sample and make inferences to the entire population. In all the presenting problems in this and future chapters dealing with inferential methods, we assume the investigators selected a random sample of individuals to study from a larger population to which they wanted to generalize.
In this chapter, we focus specifically on research questions that involve one group of subjects who are measured on one or two occasions. The best statistical approach may depend on the way we pose the research question and the assumptions we are willing to make.
We spend a lot of time on confidence intervals and hypothesis testing in this chapter in order to introduce the logic behind these two approaches. We also discuss some of the traditional topics associated with hypothesis testing, such as the errors that can be made, and we explain what P values mean. In subsequent chapters we streamline the presentation of the procedures, but we believe it is worthwhile to emphasize the details in this chapter to help reinforce the concepts.
Surveys of statistical methods used in journals indicate that the t test is one of the most commonly used statistical methods. The percentages of articles that use the t test range from 10% to more than 60%. Williams and colleagues (1997) noted a number of problems in using the t test, including a lack of discussion of assumptions in more than 85% of the articles, and Welch and Gabbe (1996) found a number of errors in using the t test when a nonparametric procedure is called for. Thus, being able to evaluate the use of tests comparing means—whether they are used properly and how to interpret the results—is an important skill for medical practitioners.
We depart from some of the traditional texts and present formulas in terms of sample statistics rather than population parameters. We also use the formulas that best reflect the concepts rather than the ones that are easiest to calculate, for the very reason that calculations are not the important issue.
Mean in One Group When the Observations Are Normally Distributed
Dennison and colleagues (1997) wanted to estimate the average consumption of various beverages in 2- and 5-year-old children and to determine whether nutritional intake in the children in their study differed from that reported in a national study of nutrition (NHANES III). Some of their findings are given in Table 5–1. Focusing specifically on the 2-year-olds, their research questions were: (1) How confident can we be that the observed mean fruit juice consumption is 5.97 oz/day? and, (2) Is the mean energy intake (1242 kcal) in their study of 2-year-olds significantly different from 1286 kcal, the value reported in NHANES III? Stated differently, do the measurements of energy intake in their study of 2-year-old children come from the same population as the measurements in NHANES III? We will use the t distribution to form confidence limits and perform statistical tests to answer these kinds of research questions.
| Row | Weight | Height | Juice | Soda | Energy | Age |
|---|---|---|---|---|---|---|
| 1 | 30.75 | 92.90 | 2.00 | 1.14 | 754.38 | 2.00 |
| 2 | 29.25 | 92.80 | 0.21 | 0.00 | 784.07 | 2.00 |
| 3 | 32.75 | 91.40 | 8.43 | 0.21 | 804.94 | 2.00 |
| 4 | 24.50 | 80.70 | 4.07 | 5.21 | 846.47 | 2.00 |
| 5 | 26.00 | 86.10 | 0.00 | 1.00 | 871.25 | 2.00 |
| 6 | 29.75 | 86.40 | 4.57 | 0.43 | 880.52 | 2.00 |
| 7 | 26.00 | 84.50 | 4.19 | 1.29 | 906.89 | 2.00 |
| 8 | 26.75 | 90.80 | 3.57 | 1.57 | 907.95 | 2.00 |
| 9 | 25.50 | 83.80 | 10.36 | 1.14 | 909.58 | 2.00 |
| 10 | 25.00 | 81.60 | 16.43 | 0.00 | 923.18 | 2.00 |
| 11 | 28.50 | 87.10 | 1.00 | 0.00 | 930.37 | 2.00 |
| 12 | 27.00 | 87.50 | 3.57 | 2.00 | 930.92 | 2.00 |
| 13 | 24.50 | 84.70 | 5.33 | 0.00 | 944.83 | 2.00 |
| 14 | 25.25 | 88.70 | 0.64 | 1.50 | 947.55 | 2.00 |
| 15 | 26.25 | 91.60 | 3.07 | 4.36 | 984.12 | 2.00 |
| 16 | 31.00 | 93.50 | 2.21 | 0.00 | 990.46 | 2.00 |
| 17 | 28.50 | 84.60 | 4.86 | 0.00 | 992.09 | 2.00 |
| 18 | 23.50 | 82.80 | 1.07 | 0.00 | 1009.83 | 2.00 |
| 19 | 26.25 | 89.00 | 0.00 | 0.00 | 1029.15 | 2.00 |
| 20 | 30.00 | 83.10 | 1.43 | 0.86 | 1035.34 | 2.00 |
| 21 | 33.75 | 97.10 | 3.71 | 0.00 | 1037.19 | 2.00 |
| 22 | 35.00 | 88.30 | 5.14 | 0.57 | 1054.41 | 2.00 |
| 23 | 23.00 | 80.70 | 14.71 | 0.29 | 1060.85 | 2.00 |
| 24 | 32.00 | 92.60 | 10.07 | 1.07 | 1074.43 | 2.00 |
| 25 | 26.00 | 76.70 | 14.36 | 0.00 | 1087.06 | 2.00 |
| 26 | 23.25 | 86.20 | 4.79 | 0.00 | 1096.98 | 2.00 |
| 27 | 30.00 | 88.40 | 1.13 | 0.11 | 1098.76 | 2.00 |
| 28 | 34.20 | 92.50 | 5.57 | 0.86 | 1108.74 | 2.00 |
| 29 | 23.75 | 81.10 | 9.36 | 0.00 | 1110.32 | 2.00 |
| 30 | 24.75 | 83.10 | 3.43 | 3.14 | 1110.85 | 2.00 |
| 31 | 24.00 | 87.70 | 14.00 | 0.00 | 1115.39 | 2.00 |
| 32 | 36.25 | 100.00 | 4.79 | 0.86 | 1122.28 | 2.00 |
| 33 | 32.50 | 97.30 | 10.57 | 1.00 | 1133.09 | 2.00 |
| 34 | 28.00 | 84.80 | 0.00 | 1.71 | 1138.43 | 2.00 |
| 35 | 27.50 | 90.20 | 2.70 | 0.64 | 1140.86 | 2.00 |
| 36 | 30.75 | 88.50 | 8.29 | 2.57 | 1142.86 | 2.00 |
| 37 | 29.25 | 91.10 | 10.43 | 0.29 | 1156.89 | 2.00 |
| 38 | 29.50 | 87.00 | 4.36 | 0.00 | 1173.30 | 2.00 |
| 39 | 27.25 | 94.00 | 3.36 | 0.43 | 1175.76 | 2.00 |
| 40 | 25.50 | 87.30 | 13.71 | 2.86 | 1177.24 | 2.00 |
| 41 | 29.80 | 90.80 | 5.34 | 0.00 | 1184.59 | 2.00 |
| 42 | 26.75 | 88.90 | 20.04 | 2.00 | 1191.05 | 2.00 |
| 43 | 29.50 | 91.30 | 9.43 | 1.14 | 1192.12 | 2.00 |
| 44 | 32.30 | 90.50 | 6.29 | 0.00 | 1192.35 | 2.00 |
| 45 | 27.75 | 87.80 | 1.71 | 0.29 | 1192.69 | 2.00 |
| 46 | 29.75 | 88.00 | 5.71 | 0.00 | 1194.34 | 2.00 |
| 47 | 33.50 | 97.80 | 0.00 | 1.50 | 1213.32 | 2.00 |
| 48 | 29.25 | 90.70 | 4.43 | 0.00 | 1229.13 | 2.00 |
| 49 | 25.25 | 85.00 | 0.00 | 0.00 | 1235.56 | 2.00 |
| 50 | 24.50 | 88.20 | 7.14 | 2.57 | 1241.20 | 2.00 |
| 51 | 27.75 | 87.00 | 7.00 | 0.43 | 1248.31 | 2.00 |
| 52 | 30.50 | 91.50 | 10.14 | 0.21 | 1249.01 | 2.00 |
| 53 | 28.00 | 85.90 | 10.71 | 0.00 | 1253.14 | 2.00 |
| 54 | 34.50 | 94.10 | 13.57 | 0.57 | 1258.85 | 2.00 |
| 55 | 27.00 | 81.70 | 14.71 | 0.29 | 1259.94 | 2.00 |
| 56 | 32.00 | 85.50 | 12.57 | 1.14 | 1271.83 | 2.00 |
| 57 | 28.75 | 85.10 | 2.14 | 0.21 | 1285.44 | 2.00 |
| 58 | 28.75 | 92.90 | 2.10 | 0.00 | 1287.97 | 2.00 |
| 59 | 25.00 | 82.80 | 1.69 | 1.26 | 1290.07 | 2.00 |
| 60 | 27.00 | 86.30 | 3.14 | 2.00 | 1293.83 | 2.00 |
| 61 | 30.75 | 87.40 | 12.50 | 0.00 | 1308.86 | 2.00 |
| 62 | 30.00 | 91.20 | 2.36 | 0.71 | 1317.63 | 2.00 |
| 63 | 31.00 | 85.50 | 1.71 | 0.57 | 1321.53 | 2.00 |
| 64 | 24.75 | 84.00 | 6.43 | 2.57 | 1337.60 | 2.00 |
| 65 | 30.00 | 93.90 | 0.86 | 0.00 | 1348.54 | 2.00 |
| 66 | 30.50 | 89.50 | 1.29 | 0.00 | 1353.41 | 2.00 |
| 67 | 34.00 | 88.40 | 0.21 | 2.36 | 1360.29 | 2.00 |
| 68 | 31.00 | 91.10 | 1.29 | 2.00 | 1361.23 | 2.00 |
| 69 | 25.50 | 92.00 | 1.14 | 3.14 | 1366.55 | 2.00 |
| 70 | 35.00 | 97.20 | 1.86 | 0.00 | 1376.19 | 2.00 |
| 71 | 34.50 | 94.20 | 0.00 | 0.00 | 1379.75 | 2.00 |
| 72 | 31.25 | 89.00 | 3.64 | 0.90 | 1395.66 | 2.00 |
| 73 | 32.75 | 88.80 | 15.43 | 0.00 | 1401.53 | 2.00 |
| 74 | 31.25 | 93.10 | 0.00 | 0.86 | 1415.58 | 2.00 |
| 75 | 35.25 | 95.30 | 1.57 | 2.86 | 1433.81 | 2.00 |
| 76 | 28.00 | 87.00 | 12.07 | 8.86 | 1437.98 | 2.00 |
| 77 | 31.50 | 91.80 | 8.71 | 2.57 | 1448.06 | 2.00 |
| 78 | 30.00 | 93.00 | 7.43 | 1.29 | 1458.32 | 2.00 |
| 79 | 33.50 | 94.90 | 2.57 | 1.14 | 1494.85 | 2.00 |
| 80 | 28.50 | 88.40 | 14.43 | 1.07 | 1500.29 | 2.00 |
| 81 | 26.00 | 84.90 | 4.79 | 1.71 | 1502.42 | 2.00 |
| 82 | 27.50 | 86.00 | 8.64 | 1.43 | 1510.70 | 2.00 |
| 83 | 31.00 | 86.30 | 8.79 | 0.00 | 1530.82 | 2.00 |
| 84 | 26.50 | 85.90 | 13.14 | 2.86 | 1553.70 | 2.00 |
| 85 | 29.25 | 93.10 | 8.86 | 1.14 | 1595.82 | 2.00 |
| 86 | 26.00 | 86.10 | 8.39 | 4.00 | 1627.34 | 2.00 |
| 87 | 35.50 | 99.40 | 2.14 | 1.86 | 1636.00 | 2.00 |
| 88 | 28.50 | 87.80 | 3.91 | 4.14 | 1653.48 | 2.00 |
| 89 | 34.50 | 92.70 | 9.71 | 0.57 | 1676.85 | 2.00 |
| 90 | 38.25 | 99.80 | 5.50 | 2.14 | 1727.23 | 2.00 |
| 91 | 31.50 | 90.20 | 6.00 | 5.36 | 1741.91 | 2.00 |
| 92 | 31.00 | 87.60 | 8.57 | 0.00 | 1785.38 | 2.00 |
| 93 | 35.25 | 95.20 | 5.14 | 1.71 | 1788.58 | 2.00 |
| 94 | 29.25 | 86.20 | 12.86 | 1.14 | 2154.31 | 2.00 |
| 95 | 38.50 | 113.00 | 6.00 | 1.00 | 726.72 | 5.00 |
| 96 | 43.00 | 105.30 | 1.93 | 0.21 | 951.13 | 5.00 |
| 97 | 34.25 | 100.20 | 7.13 | 1.29 | 1088.53 | 5.00 |
| 98 | 34.50 | 108.60 | 7.36 | 0.43 | 1207.96 | 5.00 |
| 99 | 41.66 | 112.90 | 2.29 | 0.00 | 1261.34 | 5.00 |
| 100 | 52.75 | 121.20 | 5.57 | 0.86 | 1263.42 | 5.00 |
| 101 | 46.25 | 117.80 | 1.43 | 1.29 | 1268.58 | 5.00 |
| 102 | 43.75 | 112.60 | 4.71 | 6.21 | 1289.40 | 5.00 |
| 103 | 47.90 | 114.70 | 6.86 | 2.71 | 1295.58 | 5.00 |
| 104 | 40.25 | 105.00 | 3.00 | 1.71 | 1296.83 | 5.00 |
| 105 | 40.00 | 110.30 | 7.93 | 2.29 | 1302.36 | 5.00 |
| 106 | 42.80 | 111.30 | 0.00 | 1.14 | 1311.75 | 5.00 |
| 107 | 60.00 | 121.70 | 0.86 | 4.43 | 1312.97 | 5.00 |
| 108 | 44.50 | 109.20 | 7.43 | 0.00 | 1330.37 | 5.00 |
| 109 | 39.25 | 110.60 | 0.00 | 1.43 | 1353.62 | 5.00 |
| 110 | 46.25 | 109.70 | 0.00 | 0.00 | 1368.98 | 5.00 |
| 111 | 41.50 | 112.50 | 0.00 | 2.14 | 1391.93 | 5.00 |
| 112 | 43.00 | 112.40 | 7.43 | 0.00 | 1402.42 | 5.00 |
| 113 | 42.50 | 111.40 | 8.43 | 0.00 | 1408.37 | 5.00 |
| 114 | 40.00 | 106.20 | 10.86 | 0.40 | 1408.57 | 5.00 |
| 115 | 43.50 | 109.40 | 0.57 | 2.00 | 1412.87 | 5.00 |
| 116 | 40.25 | 111.60 | 3.50 | 1.29 | 1431.74 | 5.00 |
| 117 | 37.00 | 104.30 | 1.14 | 1.50 | 1432.49 | 5.00 |
| 118 | 44.50 | 114.70 | 8.86 | 3.14 | 1434.79 | 5.00 |
| 119 | 42.25 | 114.10 | 5.29 | 2.00 | 1439.99 | 5.00 |
| 120 | 51.00 | 115.80 | 4.43 | 0.43 | 1442.08 | 5.00 |
| 121 | 47.25 | 114.60 | 8.29 | 2.29 | 1443.55 | 5.00 |
| 122 | 49.00 | 119.00 | 1.14 | 2.29 | 1446.17 | 5.00 |
| 123 | 45.75 | 112.10 | 6.00 | 1.86 | 1448.43 | 5.00 |
| 124 | 57.00 | 112.00 | 1.57 | 1.71 | 1462.08 | 5.00 |
| 125 | 47.75 | 119.70 | 3.57 | 0.00 | 1475.16 | 5.00 |
| 126 | 38.25 | 112.10 | 1.07 | 1.29 | 1487.11 | 5.00 |
| 127 | 47.50 | 115.70 | 1.71 | 0.00 | 1489.22 | 5.00 |
| 128 | 39.00 | 108.50 | 3.36 | 1.14 | 1496.36 | 5.00 |
| 129 | 41.00 | 108.10 | 5.14 | 4.86 | 1496.74 | 5.00 |
| 130 | 40.25 | 110.80 | 11.04 | 0.86 | 1513.10 | 5.00 |
| 131 | 36.50 | 104.30 | 4.86 | 0.71 | 1521.40 | 5.00 |
| 132 | 50.25 | 117.70 | 0.29 | 0.00 | 1542.93 | 5.00 |
| 133 | 38.50 | 107.60 | 6.00 | 0.00 | 1552.84 | 5.00 |
| 134 | 31.00 | 94.50 | 3.61 | 0.64 | 1565.48 | 5.00 |
| 135 | 49.50 | 116.70 | 0.00 | 6.61 | 1579.71 | 5.00 |
| 136 | 41.00 | 108.10 | 7.71 | 5.71 | 1580.54 | 5.00 |
| 137 | 63.00 | 116.70 | 4.29 | 5.29 | 1594.05 | 5.00 |
| 138 | 46.50 | 112.40 | 0.14 | 3.43 | 1595.22 | 5.00 |
| 139 | 45.50 | 110.30 | 4.57 | 5.14 | 1604.54 | 5.00 |
| 140 | 45.00 | 110.70 | 2.00 | 1.29 | 1616.60 | 5.00 |
| 141 | 57.75 | 126.10 | 3.06 | 1.53 | 1621.34 | 5.00 |
| 142 | 53.80 | 123.90 | 4.29 | 4.57 | 1627.36 | 5.00 |
| 143 | 55.50 | 108.00 | 13.00 | 3.43 | 1652.53 | 5.00 |
| 144 | 45.50 | 108.90 | 15.43 | 3.86 | 1653.05 | 5.00 |
| 145 | 47.00 | 112.90 | 6.86 | 3.43 | 1661.32 | 5.00 |
| 146 | 41.00 | 108.90 | 9.21 | 0.00 | 1670.65 | 5.00 |
| 147 | 47.20 | 114.40 | 3.71 | 2.00 | 1681.05 | 5.00 |
| 148 | 47.00 | 114.10 | 5.93 | 7.43 | 1685.25 | 5.00 |
| 149 | 35.50 | 104.50 | 2.86 | 1.14 | 1686.05 | 5.00 |
| 150 | 48.25 | 111.70 | 0.86 | 1.29 | 1703.80 | 5.00 |
| 151 | 42.25 | 111.80 | 0.00 | 0.86 | 1721.98 | 5.00 |
| 152 | 36.25 | 104.60 | 2.29 | 1.14 | 1725.28 | 5.00 |
| 153 | 39.25 | 108.10 | 5.79 | 1.64 | 1729.69 | 5.00 |
| 154 | 38.00 | 107.60 | 19.14 | 0.43 | 1762.36 | 5.00 |
| 155 | 44.00 | 118.10 | 10.57 | 1.14 | 1763.84 | 5.00 |
| 156 | 42.25 | 107.10 | 6.00 | 1.14 | 1769.47 | 5.00 |
| 157 | 36.50 | 94.30 | 22.30 | 0.00 | 1860.29 | 5.00 |
| 158 | 39.25 | 105.60 | 0.86 | 2.14 | 1873.10 | 5.00 |
| 159 | 42.50 | 109.40 | 0.00 | 0.43 | 1875.67 | 5.00 |
| 160 | 40.00 | 105.80 | 2.29 | 3.14 | 1877.10 | 5.00 |
| 161 | 39.75 | 107.40 | 5.00 | 1.71 | 1879.66 | 5.00 |
| 162 | 43.00 | 107.50 | 0.57 | 2.29 | 1919.29 | 5.00 |
| 163 | 41.20 | 109.80 | 10.93 | 2.43 | 1941.62 | 5.00 |
| 164 | 39.00 | 110.50 | 4.64 | 4.71 | 1960.26 | 5.00 |
| 165 | 42.50 | 113.60 | 1.71 | 8.50 | 1988.63 | 5.00 |
| 166 | 41.75 | 111.30 | 4.71 | 3.57 | 2206.71 | 5.00 |
| 167 | 40.50 | 104.80 | 8.57 | 4.00 | 2285.65 | 5.00 |
| 168 | 43.75 | 111.70 | 7.71 | 4.00 | 2490.33 | 5.00 |
![]() Before discussing research questions involving means, let’s think about what it takes to convince us that a mean in a study is significantly different from a norm or population mean. If we want to know whether the mean energy intake in 2-year-old children in our practice is different from the mean in a national nutrition study, what evidence is needed to conclude that energy intake is really different in our group and not just a random occurrence? If the mean energy intake is much larger or smaller than the mean in the national nutrition study, such as the situation in Figure 5–1A, we will probably conclude that the difference is real. What if the difference is relatively moderate, as is the situation in Figure 5–1B?
Before discussing research questions involving means, let’s think about what it takes to convince us that a mean in a study is significantly different from a norm or population mean. If we want to know whether the mean energy intake in 2-year-old children in our practice is different from the mean in a national nutrition study, what evidence is needed to conclude that energy intake is really different in our group and not just a random occurrence? If the mean energy intake is much larger or smaller than the mean in the national nutrition study, such as the situation in Figure 5–1A, we will probably conclude that the difference is real. What if the difference is relatively moderate, as is the situation in Figure 5–1B?
What other factors can help us? Figure 5–1B gives a clue: The sample values vary substantially, compared with Figure 5–1A, in which there is less variation. A smaller standard deviation may lead to a real difference, even though the difference is relatively small. For the variability to be small, subjects must be relatively similar (homogeneous) and the method of measurement must be relatively precise. In contrast, if the characteristic measured varies widely from one person to another or if the measuring device is relatively crude, the standard deviations will be greater, and we will need to observe a greater difference to be convinced that the difference is real and not just a random occurrence.
Another factor is the number of patients included in the sample. Most of us have greater intuitive confidence in findings that are based on a larger rather than a smaller sample, and we will demonstrate the sound statistical reasons for this confidence.
To summarize, three factors play a role in deciding whether an observed mean differs from a norm: (1) the difference between the observed mean and the norm, (2) the amount of variability among subjects, and (3) the number of subjects in the study. We will see later in this chapter that the first two factors are important when we want to estimate the needed sample size before beginning a study.
The t test is used a great deal in all areas of science. The t distribution is similar in shape to the z distribution introduced in the previous chapter, and one of its major uses is to answer research questions about means. Because we use the t distribution and the t test in several chapters, we need a basic understanding of t.
The t test is sometimes called “Student’s t test” after the person who first studied the distribution of means from small samples in 1890. Student was really a mathematician named William Gosset who worked for the Guiness Brewery; he was forced to use the pseudonym Student because of company policy prohibiting employees from publishing their work. Gosset discovered that when observations come from a normal distribution, the means are normally distributed only if the true standard deviation in the population is known. When the true standard deviation is not known and researchers use the sample standard deviation in its place, the means are no longer normally distributed. Gosset named the distribution of means when the sample standard deviation is used the t distribution.
If you think about it, you will recognize that we almost always use samples instead of populations in medical research. As a result, we seldom know the true standard deviation and almost always use the sample standard deviation. Our conclusions are therefore more likely to be accurate if we use the t distribution rather than the normal distribution, although the difference between t and z becomes very small when n is greater than 30.
The formula (or critical ratio) for the t test has the observed mean (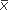 ) minus the hypothesized value of the population mean (μ) in the numerator, and the standard error of the mean in the denominator. The symbol μ stands for the true mean in the population; it is the Greek letter mu, pronounced “mew.” The formula for the t test is
) minus the hypothesized value of the population mean (μ) in the numerator, and the standard error of the mean in the denominator. The symbol μ stands for the true mean in the population; it is the Greek letter mu, pronounced “mew.” The formula for the t test is
![]() We know the standard normal, or z, distribution is symmetric with a mean of 0 and a standard deviation of 1. The t distribution is also symmetric and has a mean of 0, but its standard deviation is larger than 1. The precise size of the standard deviation depends on a complex concept related to the sample size, called degrees of freedom (df), which is related to the number of times sample information is used. Because sample information is used once to estimate the standard deviation, the t distribution for one group, it has n – 1 df.
We know the standard normal, or z, distribution is symmetric with a mean of 0 and a standard deviation of 1. The t distribution is also symmetric and has a mean of 0, but its standard deviation is larger than 1. The precise size of the standard deviation depends on a complex concept related to the sample size, called degrees of freedom (df), which is related to the number of times sample information is used. Because sample information is used once to estimate the standard deviation, the t distribution for one group, it has n – 1 df.
Because the t distribution has a larger standard deviation, it is wider and its tails are higher than those for the z distribution. As the sample size increases to 30 or more, the df also increase, and the t distribution becomes almost the same as the standard normal distribution, and either t or z can be used. Generally the t distribution is used in medicine, even when the sample size is 30 or greater, and we will follow that practice in this book. Computer programs, such as Visual Statistics (module on continuous distributions) or ConStats that allow for the plotting of different distributions, can be used to generate t distributions for different sample sizes in order to compare them, as we did in Figure 5–2.
When using the t distribution to answer research questions, we need to find the area under the curve, just as with the z distribution. The area can be found by using calculus to integrate a mathematical function, but fortunately we do not need to do so. Formerly, statisticians used tables (as we do when illustrating some points in this book), but today most of us use computer programs. Table A–3 in Appendix A gives the critical values for the t distribution corresponding to areas in the tail of the distribution equal to 0.10, 0.05, 0.02, 0.01, and 0.001 for two-tailed, or two-sided, tests (half that size for one-tailed tests or one-sided tests).
We assume that the observations are normally distributed in order to use the t distribution. When the observations are not normally distributed, a nonparametric statistical test, called the sign test, is used instead; see the section titled, “What to Do When Observations Are Not Normally Distributed.”
![]() Confidence intervals are used increasingly for research involving means, proportions, and other statistics in medicine, and we will encounter them in subsequent chapters. Thus, it is important to understand the basics. The general format for confidence intervals for one mean is
Confidence intervals are used increasingly for research involving means, proportions, and other statistics in medicine, and we will encounter them in subsequent chapters. Thus, it is important to understand the basics. The general format for confidence intervals for one mean is
The confidence coefficient is a number related to the level of confidence we want; typical values are 90%, 95%, and 99%, with 95% being the most common. Refer to Table A–3 to find the confidence coefficients. For 95% confidence, we want the value that separates the central 95% of the distribution from the 5% in the two tails; with 10 df this value is 2.228. As the sample size becomes very large, the confidence coefficient for a 95% confidence interval is the same as the z distribution, 1.96, as shown in the bottom line of Table A–3.
Recall from Chapter 4 that the standard error of the mean (SE) is the standard deviation divided by the square root of the sample size and is used to estimate how much the mean can be expected to vary from one sample to another. Using  as the observed (sample) mean, the formula for a 95% confidence interval for the true mean is
as the observed (sample) mean, the formula for a 95% confidence interval for the true mean is
where t stands for the confidence coefficient (critical value from the t distribution), which, as we saw earlier, depends on the df (which in turn depend on the sample size).
Using the data from Dennison and coworkers (1997) in Table 5–1, we discover that the mean is 5.97 oz/day and the standard deviation is 4.77. The df for the mean in a single group is n – 1, or 94 – 1 = 93 in our example. In Table A–3, the value corresponding to 95% confidence limits is about halfway between 2.00 for 60 df and 1.98 for 120 df, so we use 1.99. Using these numbers in the preceding formula, we get
or approximately 4.99 to 6.95 oz/day. We interpret this confidence interval as follows: in other samples of 2-year-old children, Dennison and coworkers (or other researchers) would almost always observe mean juice consumption different from the one in this study. They would not know the true mean, of course. If they calculated a 95% confidence interval for each mean, however, 95% of these confidence intervals would contain the true mean. They can therefore have 95% confidence that the interval from 4.99 to 6.95 oz/day contains the actual mean juice consumption in 2-year-old children. Using 4.99 to 6.95 oz/day to express the confidence interval is better than 4.99–6.95 oz/day, which can become confusing if the interval has negative signs.
Medical researchers often use error graphs to illustrate means and confidence intervals. Box 5–1 shows an error graph of the mean fruit juice consumption among 2-year-old children, along with the 95% confidence limits. You can replicate this analysis using the “Dennison” file on the CD-ROM [available only with the book] and the SPSS Explore procedure.
| One-Sample Test | ||||||
| Test value = 0 | ||||||
| 95% Confidence Interval of the Difference | ||||||
| t | df | Significance (2-tailed) | Mean Difference | Lower | Upper | |
| Juice | 12.129 | 93 | .000 | 5.9714 | 4.9938 | 6.9490 |
 | ||||||
There is nothing sacred about 95% confidence intervals; they simply are the ones most often reported in the medical literature. If researchers want to be more confident that the interval contains the true mean, they can use a 99% confidence interval. Will this interval be wider or narrower than the interval corresponding to 95% confidence?
Some investigators test hypotheses instead of finding and reporting confidence intervals. The conclusions are the same, regardless of which method is used. More and more, statisticians recommend confidence intervals because they actually provide more information than hypothesis tests. Some researchers still prefer hypothesis tests, possibly because tests have been used traditionally. We will return to this point after we illustrate the procedure for testing a hypothesis concerning the mean in a single sample.
As with confidence limits, the purpose of a hypothesis test is to permit generalizations from a sample to the population from which the sample came. Both statistical hypothesis testing and estimation make certain assumptions about the population and then use probabilities to estimate the likelihood of the results obtained in the sample, given these assumptions.
To illustrate hypothesis testing, we use the energy intake data from Dennison and coworkers (1997) in Table 5–1. We use these observations to test whether the mean energy intake in 2-year-olds in this study is different from the mean energy intake in the NHANES III data shown in Table 5–2, to be the norm. Another way to state the research question is: On average, do 2-year-old children in the sample studied by Dennison and coworkers have the different levels of energy intake as 2-year-olds in the NHANES III study?
| Dietary Variable | Our Study 2.0–2.9 years (n = 94) | NHANES IIIa 1.0–2.9 years (n = 424) | Our Study 5.0–5.9 years (n = 74) | NHANES IIIa 3.0–5.0 years (n = 425) |
|---|---|---|---|---|
| Energy (kcal) | 1242 ± 30b | 1286 ± 22 | 1549 ± 34 | 1573 ± 28 |
| Protein (g) | 43 ± 1.3 | 47 ± 0.9 | 53 ± 1.6 | 55 ± 1.2 |
| (% kcal) | 14.0 ± 0.2 | 14.7 ± 0.2 | 13.7 ± 0.2 | 14.1 ± 0.21 |
| Carbohydrate (g) | 169 ± 4.6 | 171 ± 3.3 | 211 ± 5.1 | 215 ± 4.0 |
| (% kcal) | 54.4 ± 0.6 | 53.9 ± 0.6 | 54.7 ± 0.6 | 55.3 ± 0.5 |
| Total fat (g) | 46 ± 1.3 | 49 ± 1.1 | 57 ± 1.6 | 58 ± 1.4 |
| (% kcal) | 33.2 ± 0.5 | 33.5 ± 0.4 | 33.0 ± 0.5 | 32.7 ± 0.4 |
| Saturated fat (g) | 19 ± 0.6 | 20 ± 0.5 | 23 ± 0.7 | 22 ± 0.6 |
| (% kcal) | 13.7 ± 0.3 | 13.8 ± 0.2 | 13.2 ± 0.3 | 12.5 ± 0.2 |
| Cholesterol | 155 ± 6.7 | 168 ± 70 | 173 ± 7.2 | 175 ± 7.2 |
| (mg/1000 kcal) | 126 ± 5.1 | 131c | 111 ± 4.1 | 111c |
![]() Statistical hypothesis testing seems to be the reverse of our nonstatistical thinking. We first assume that the mean energy intake is the same as in NHANES III (1286 kcal), and then we find the probability of observing mean energy intake equal to 1242 kcal in a sample of 94 children, given this assumption. If the probability is large, we conclude that the assumption is justified and the mean energy intake in the study is not statistically different from that reported by NHANES III. If the probability is small, however—such as 1 out of 20 (0.05) or 1 out of 100 (0.01)—we conclude that the assumption is not justified and that there really is a difference; that is, 2-year-old children in the Dennison and coworkers study have a mean energy intake different from those in NHANES III. Following a brief discussion of the assumptions we make when using the t distribution, we will use the Dennison and coworkers study to illustrate the steps in hypothesis testing.
Statistical hypothesis testing seems to be the reverse of our nonstatistical thinking. We first assume that the mean energy intake is the same as in NHANES III (1286 kcal), and then we find the probability of observing mean energy intake equal to 1242 kcal in a sample of 94 children, given this assumption. If the probability is large, we conclude that the assumption is justified and the mean energy intake in the study is not statistically different from that reported by NHANES III. If the probability is small, however—such as 1 out of 20 (0.05) or 1 out of 100 (0.01)—we conclude that the assumption is not justified and that there really is a difference; that is, 2-year-old children in the Dennison and coworkers study have a mean energy intake different from those in NHANES III. Following a brief discussion of the assumptions we make when using the t distribution, we will use the Dennison and coworkers study to illustrate the steps in hypothesis testing.
![]() For the t distribution or the t test to be used, observations should be normally distributed. Many computer programs, such as NCSS and SPSS, overlay a plot of the normal distribution on a histogram of the data. Often it is possible to look at a histogram or a box-and-whisker plot and make a judgment call. Sometimes we know the distribution of the data from past research, and we can decide whether the assumption of normality is reasonable. This assumption can be tested empirically by plotting the observations on a normal probability graph, called a Lilliefors graph (Conover, 1999, or using several statistical tests of normality. The NCSS computer program produces a normal probability plot as part of the Descriptive Statistics Report, which we illustrate in the section titled, “Mean Difference When Observations Are Not Normally Distributed” (see Box 5–2), and reports the results of several statistical tests. SPSS has a routine to test normality that is part of the Explore Plots option. It is always a good idea to plot data before beginning the analysis in case some strange values are present that need to be investigated.
For the t distribution or the t test to be used, observations should be normally distributed. Many computer programs, such as NCSS and SPSS, overlay a plot of the normal distribution on a histogram of the data. Often it is possible to look at a histogram or a box-and-whisker plot and make a judgment call. Sometimes we know the distribution of the data from past research, and we can decide whether the assumption of normality is reasonable. This assumption can be tested empirically by plotting the observations on a normal probability graph, called a Lilliefors graph (Conover, 1999, or using several statistical tests of normality. The NCSS computer program produces a normal probability plot as part of the Descriptive Statistics Report, which we illustrate in the section titled, “Mean Difference When Observations Are Not Normally Distributed” (see Box 5–2), and reports the results of several statistical tests. SPSS has a routine to test normality that is part of the Explore Plots option. It is always a good idea to plot data before beginning the analysis in case some strange values are present that need to be investigated.
| Tests of Assumptions about Difference Section | |||
|---|---|---|---|
| Assumption | Value | Probability | Decision (5%) |
| Skewness Normality | –3.8054 | 0.000142 | Reject normality |
| Kurtosis Normality | 2.8091 | 0.004968 | Reject normality |
| Omnibus Normality | 22.3724 | 0.000014 | Reject normality |
You may wonder why normality matters. What happens if the t distribution is used for observations that are not normally distributed? With 30 or more observations, the central limit theorem (Chapter 4) tells us that means are normally distributed, regardless of the distribution of the original observations. So, for research questions concerning the mean, the central limit theorem basically says that we do not need to worry about the underlying distribution with reasonable sample sizes. However, using the t distribution with observations that are not normally distributed and when the sample size is fewer than 30 can lead to confidence intervals that are too narrow. In this situation, we erroneously conclude that the true mean falls in a narrower range than is really the case. If the observations deviate from the normal distribution in only minor ways, the t distribution can be used anyway, because it is robust for nonnormal data. (Robustness means we can draw the proper conclusion even when all our assumptions are not met.)
Hypothesis Testing
We now illustrate the steps in testing a hypothesis and discuss some related concepts using data from the study by Dennison and coworkers.
![]() A statistical hypothesis is a statement of belief about population parameters. Like the term “probability,” the term “hypothesis” has a more precise meaning in statistics than in everyday use.
A statistical hypothesis is a statement of belief about population parameters. Like the term “probability,” the term “hypothesis” has a more precise meaning in statistics than in everyday use.
Step 1: State the research question in terms of statistical hypotheses. The null hypothesis, symbolized by H0, is a statement claiming that there is no difference between the assumed or hypothesized value and the population mean; null means “no difference.” The alternative hypothesis, which we symbolize by H1 (some textbooks use HA) is a statement that disagrees with the null hypothesis.
If the null hypothesis is rejected as a result of sample evidence, then the alternative hypothesis is concluded. If the evidence is insufficient to reject the null hypothesis, it is retained but not accepted per se. Scientists distinguish between not rejecting and accepting the null hypothesis; they argue that a better study may be designed in which the null hypothesis will be rejected. Traditionally, we therefore do not accept the null hypothesis from current evidence; we merely state that it cannot be rejected.
For the Dennison and coworkers study, the null and alternative hypotheses are as follows:
H0: The mean energy intake in 2-year-old children in the study, μ1, is not different from the norm (mean in NHANES III), μ0, written μ1 = μ0.
H1: The mean energy intake in 2-year-old children in the Dennison and coworkers study, μ1, is different from the norm (mean in NHANES III), μ0, written μ1 ≠ μ0. (Recall that μ stands for the true mean in the population.)
These hypotheses are for a two-tailed (or nondirectional) test: The null hypothesis will be rejected if mean energy intake is sufficiently greater than 1286 kcal or if it is sufficiently less than 1286 kcal. A two-tailed test is appropriate when investigators do not have an a priori expectation for the value in the sample; they want to know if the sample mean differs from the population mean in either direction.
A one-tailed (or directional) test can be used when investigators have an expectation about the sample value, and they want to test only whether it is larger or smaller than the mean in the population. Examples of an alternative hypothesis are H1: The mean energy intake in 2-year-old children in the Dennison and coworkers study, μ1, is larger than the norm (mean in NHANES III), μ0, sometimes written μ1 > μ0
or
H1: The mean energy intake in 2-year-old children in the Dennison and coworkers study, μ1, is not larger than the norm (mean in NHANES III), μ0, sometimes written as μ1 ≤ μ0.
A one-tailed test has the advantage over a two-tailed test of obtaining statistical significance with a smaller departure from the hypothesized value, because there is interest in only one direction. Whenever a one-tailed test is used, it should therefore make sense that the investigators really were interested in a departure in only one direction before the data were examined. The disadvantage of a one-tailed test is that once investigators commit themselves to this approach, they are obligated to test only in the hypothesized direction. If, for some unexpected reason, the sample mean departs from the population mean in the opposite direction, the investigators cannot rightly claim the departure as significant. Medical researchers often need to be able to test for possible unexpected adverse effects as well as the anticipated positive effects, so they most frequently choose a two-tailed hypothesis even though they have an expectation about the direction of the departure. A graphic representation of a one-tailed and a two-tailed test is given in Figure 5–3.
Figure 5–3.
Defining areas of acceptance and rejection in hypothesis testing using α = 0.05. A: Two-tailed or nondirectional. B: One-tailed or directional lower tail. C: One-tailed or directional upper tail. (Data, used with permission, from Dennison BA, Rockwell HL, Baker SL: Excess fruit juice consumption by preschool-aged children is associated with short stature and obesity. Pediatrics 1997;99:15–22. Graphs produced using the Visualizing Continuous Distributions module in Visual Statistics, a program published by McGraw-Hill Companies; used with permission.)
Step 2: Decide on the appropriate test statistic. Some texts use the term “critical ratio” to refer to test statistics. Choosing the right test statistic is a major topic in statistics, and subsequent chapters focus on which test statistics are appropriate for answering specific kinds of research questions.
We decide on the appropriate statistic as follows. Each test statistic has a probability distribution. In this example, the appropriate test statistic is based on the t distribution because we want to make inferences about a mean and do not know the population standard deviation. The t test is the test statistic for testing one mean; it is the difference between the sample mean and the hypothesized mean divided by the standard error.
Step 3: Select the level of significance for the statistical test. The level of significance, when chosen before the statistical test is performed, is called the alpha value, denoted by α (Greek letter alpha); it gives the probability of incorrectly rejecting the null hypothesis when it is actually true (and concluding there is a difference when there is not). This probability should be small, because we do not want to reject the null hypothesis when it is true. Traditional values used for α are 0.05, 0.01, and 0.001. We will use α = 0.05.
Step 4: Determine the value the test statistic must attain to be declared significant. This significant value is also called the critical value of the test statistic. Determining the critical value is simple (we already found it when we calculated a 95% confidence interval), but detailing the reasoning behind the process is instructive. Each test statistic has a distribution; the distribution of the test statistic is divided into an area of (hypothesis) acceptance and an area of (hypothesis) rejection. The critical value is the dividing line between the areas.
An illustration should help clarify the idea. The test statistic in our example follows the t distribution; α is 0.05; and a two-tailed test was specified. Thus, the area of acceptance is the central 95% of the t distribution, and the areas of rejection are the 2.5% areas in each tail (see Figure 5–3). From Table A–3, the value of t (with n – 1 or 94 – 1 = 93 df) that defines the central 95% area is between –1.99 and 1.99, as we found for the 95% confidence interval. Thus, the portion of the curve below –1.99 contains the lower 2.5% of the area of the t distribution with 93 df, and the portion above +1.99 contains the upper 2.5% of the area. The null hypothesis (that the mean energy intake of the group studied by Dennison and coworkers is equal to 1286 kcal as reported in the NHANES III study) will therefore be rejected if the critical value of the test statistic is less than –1.99 or if it is greater than +1.99.
In practice, however, almost everyone uses computers to do their statistical analyses. As a result, researchers do not usually look up the critical value before doing a statistical test. Although researchers need to decide beforehand the alpha level they will use to conclude significance, in practice they wait and see the more exact P value calculated by the computer program. We discuss the P value in the following sections.
Step 5: Perform the calculation. To summarize, the mean energy intake among the 94 two-year-old children studied by Dennison and coworkers was 1242 kcal with standard deviation 256 and standard error 26.4.a We compare this value with the assumed population value of 1286 kcal. Substituting these values in the test statistic yields
aWhere does the value of 26.4 come from? Recall from Chapter 4 that the standard error of the mean, SE, is the standard deviation of the mean, not the standard deviation of the original observations. We calculate the standard error of the mean by dividing the standard deviation by the square root of the sample size:
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree





