Key Concepts
 The choice of statistical methods depends on the research question, the scales on which the variables are measured, and the number of variables to be analyzed.
The choice of statistical methods depends on the research question, the scales on which the variables are measured, and the number of variables to be analyzed.
 Many of the advanced statistical procedures can be interpreted as an extension or modification of multiple regression analysis.
Many of the advanced statistical procedures can be interpreted as an extension or modification of multiple regression analysis.
 Many of the statistical methods used for questions with one independent variable have direct analogies with methods for multiple independent variables.
Many of the statistical methods used for questions with one independent variable have direct analogies with methods for multiple independent variables.
 The term “multivariate” is used when more than one independent variable is analyzed.
The term “multivariate” is used when more than one independent variable is analyzed.
 Multiple regression is a simple and ideal method to control for confounding variables.
Multiple regression is a simple and ideal method to control for confounding variables.
 Multiple regression coefficients indicate whether the relationship between the independent and dependent variables is positive or negative.
Multiple regression coefficients indicate whether the relationship between the independent and dependent variables is positive or negative.
 Dummy, or indicator, coding is used when nominal variables are used in multiple regression.
Dummy, or indicator, coding is used when nominal variables are used in multiple regression.
 Regression coefficients indicate the amount the change in the dependent variable for each one-unit change in the X variable, holding other independent variables constant.
Regression coefficients indicate the amount the change in the dependent variable for each one-unit change in the X variable, holding other independent variables constant.
 Multiple regression measures a linear relationship only.
Multiple regression measures a linear relationship only.
 The Multiple R statistic is the best indicator of how well the model fits the data—how much variance is accounted for.
The Multiple R statistic is the best indicator of how well the model fits the data—how much variance is accounted for.
 Several methods can be used to select variables in a multivariate regression.
Several methods can be used to select variables in a multivariate regression.
 Polynomial regression can be used when the relationship is curvilinear.
Polynomial regression can be used when the relationship is curvilinear.
 Cross-validation tell us how applicable the model will be if we used it in another sample of subjects.
Cross-validation tell us how applicable the model will be if we used it in another sample of subjects.
 A good rule of thumb is to have ten times as many subjects as variables.
A good rule of thumb is to have ten times as many subjects as variables.
 Analysis of covariance controls for confounding variables; it can be used as part of analysis of variance or in multiple regression.
Analysis of covariance controls for confounding variables; it can be used as part of analysis of variance or in multiple regression.
 Logistic regression predicts a nominal outcome; it is the most widely used regression method in medicine.
Logistic regression predicts a nominal outcome; it is the most widely used regression method in medicine.
 The regression coefficients in logistic regression can be transformed to give odds ratios.
The regression coefficients in logistic regression can be transformed to give odds ratios.
 The Cox model is the multivariate analogue of the Kaplan–Meier curve; it predicts time-dependent outcomes when there are censored observations.
The Cox model is the multivariate analogue of the Kaplan–Meier curve; it predicts time-dependent outcomes when there are censored observations.
 The Cox model is also called the proportional hazard model; it is one of the most important statistical methods in medicine.
The Cox model is also called the proportional hazard model; it is one of the most important statistical methods in medicine.
 Meta-analysis provides a way to combine the results from several studies in a quantitative way and is especially useful when studies have come to opposite conclusions or are based on small samples.
Meta-analysis provides a way to combine the results from several studies in a quantitative way and is especially useful when studies have come to opposite conclusions or are based on small samples.
 An effect size is a measure of the magnitude of differences between two groups; it is a useful concept in estimating sample sizes.
An effect size is a measure of the magnitude of differences between two groups; it is a useful concept in estimating sample sizes.
 The Cochrane Collection is a set of very well designed meta-analyses and is available at libraries and online.
The Cochrane Collection is a set of very well designed meta-analyses and is available at libraries and online.
 Several methods are available when the goal is to classify subjects into groups.
Several methods are available when the goal is to classify subjects into groups.
 Multivariate analysis of variance, or MANOVA, is analogous to using ANOVA when there are several dependent variables.
Multivariate analysis of variance, or MANOVA, is analogous to using ANOVA when there are several dependent variables.
Presenting Problems
In Chapter 8 we examined the study by Jackson and colleagues (2002) who evaluated the relationship between BMI and percent body fat. Please refer to that chapter for more details on the study. We found a significant relationship between these two measures and calculated a correlation coefficient of r = 0.73. These investigators knew, however, that variables other than BMI may also affect the relationship between BMI and percent body fat and developed separate models for men and women. We use their data in this chapter to illustrate two important procedures: multiple regression to control possible confounding variables, and polynomial regression to model the nonlinear relationship we noted in Chapter 8. Data are on the CD-ROM [available only with the book] in a file entitled “Jackson.”
Soderstrom and coinvestigators (1997) wanted to develop a model to identify trauma patients who are likely to have a blood alcohol concentration (BAC) in excess of 50 mg/dL. They evaluated data from a clinical trauma registry and toxicology database at a level I trauma center. Such patients might be candidates for alcohol and drug abuse and dependence treatment and intervention programs.
Data, including BAC, were available on 11,062 patients of whom approximately 71% were male and 65% were white. The mean age was 35 years with a standard deviation of 17 years. Type of injury was classified as unintentional, typically accidental (78.2%), or intentional, including suicide attempts (21.8%). Of these patients, 3180 (28.7%) had alcohol detected in the blood, and 91.2% of those patients had a BAC in excess of 50 mg/dL. Among the patients with a BAC > 50, percentages of men and whites did not differ appreciably from the entire sample; however, the percentage of intentional injuries in this group was higher (28.9%). We use a random sample of data provided by the investigators to illustrate the calculation and interpretation of the logistic model, the statistical method they used to develop their predictive model. Data are in a file called “Soderstrom” on the CD-ROM [available only with the book].
In the previous chapter we used data from a study by Crook and colleagues (1997) to illustrate the Kaplan–Meier survival analysis method. These investigators studied the correlation between both the pretreatment prostate-specific antigen (PSA) and posttreatment nadir PSA levels in men with localized prostate cancer who were treated using external beam radiation therapy. The Gleason histologic scoring system was used to classify tumors on a scale of 2 to 10. Please refer to that Chapter 9 for more details. The investigators wanted to examine factors other than tumor stage that might be associated with treatment failure, and we use observations from their study to describe an application of the Cox proportional hazard model. Data on the patients are given in the file entitled “Crook” on the CD-ROM [available only with the book].
The use of central venous catheters to administer parenteral nutrition, fluids, or drugs is a common medical practice. Catheter-related bloodstream infections (CR-BSI) are a serious complication estimated to occur in about 200,000 patients each year. Many studies have suggested that impregnation of the catheter with the antiseptic chlorhexidine/silver sulfadiazine reduces bacterial colonization, but only one study has shown a significant reduction in the incidence of bloodstream infections.
It is difficult for physicians to interpret the literature when studies report conflicting results about the benefits of a clinical intervention or practice. As you now know, studies frequently fail to find significance because of low power associated with small sample sizes. Traditionally, conflicting results in medicine are dealt with by reviewing many studies published in the literature and summarizing their strengths and weaknesses in what are commonly called review articles. Veenstra and colleagues (1999) used a more structured method to combine the results of several studies in a statistical manner. They applied meta-analysis to 11 randomized, controlled clinical trials, comparing the incidence of bloodstream infection in impregnated catheters versus nonimpregnated catheters, so that overall conclusions regarding efficacy of the practice could be drawn. The section titled “Meta-Analysis” summarizes the results.
Purpose of the Chapter
The purpose of this chapter is to present a conceptual framework that applies to almost all the statistical procedures discussed so far in this text. We also describe some of the more advanced techniques used in medicine.
![]() The previous chapters illustrated statistical techniques that are appropriate when the number of observations on each subject in a study is limited. For example, a t test is used when two groups of subjects are studied and the measure of interest is a single numerical variable—such as in Presenting Problem 1 in Chapter 6, which discussed differences in pulse oximetry in patients who did and did not have a pulmonary embolism(Kline et al, 2002). When the outcome of interest is nominal, the chi-square test can be used—such as the Lapidus et al (2002) study of screening for domestic violence in the emergency department (Chapter 6 Presenting Problem 3). Regression analysis is used to predict one numerical measure from another, such as in the study predicting insulin sensitivity in hyperthyroid women (Gonzalo et al, 1996; Chapter 7 Presenting Problem 2).
The previous chapters illustrated statistical techniques that are appropriate when the number of observations on each subject in a study is limited. For example, a t test is used when two groups of subjects are studied and the measure of interest is a single numerical variable—such as in Presenting Problem 1 in Chapter 6, which discussed differences in pulse oximetry in patients who did and did not have a pulmonary embolism(Kline et al, 2002). When the outcome of interest is nominal, the chi-square test can be used—such as the Lapidus et al (2002) study of screening for domestic violence in the emergency department (Chapter 6 Presenting Problem 3). Regression analysis is used to predict one numerical measure from another, such as in the study predicting insulin sensitivity in hyperthyroid women (Gonzalo et al, 1996; Chapter 7 Presenting Problem 2).
Alternatively, each of these examples can be viewed conceptually as involving a set of subjects with two observations on each subject: (1) for the t test, one numerical variable, pulse oximetry, and one nominal (or group membership) variable, development of pulmonary embolism; (2) for the chi-square test, two nominal variables, training in domestic violence and screening in the emergency department; (3) for regression, two numerical variables, insulin sensitivity and body mass index. It is advantageous to look at research questions from this perspective because ideas are analogous to situations in which many variables are included in a study.
To practice viewing research questions from a conceptual perspective, let us reconsider Presenting Problem 1 in Chapter 7 by Woeber (2002). The objective was to determine whether differences exist in serum free T4 concentrations in patients who had thyroiditis with normal serum TSH values and not taking l-T4 replacement, had normal TSH values and were taking l-T4 replacement therapy, or had normal thyroid and serum TSH levels. The research question in this study may be viewed as involving a set of subjects with two observations per subject: one numerical variable, serum free T4 concentrations, and one ordinal (or group membership) variable, thyroid status, with three categories. If only two categories were included for thyroid status, the t test would be used. With more than two groups, however, one-way analysis of variance (ANOVA) is appropriate.
Many problems in medicine have more than two observations per subject because of the complexity involved in studying disease in humans. In fact, many of the presenting problems used in this text have multiple observations, although we chose to simplify the problems by examining only selected variables. One method involving more than two observations per subject has already been discussed: two-way ANOVA. Recall that in Presenting Problem 2 in Chapter 7 insulin sensitivity was examined in overweight and normal weight women with and without hyperthyroid disease (Gonzalo et al, 1996). For this analysis, the investigators classified women according to two nominal variables (weight status and thyroid status, both measured as normal or higher than normal) and one numerical variable, insulin sensitivity. (Although both weight and thyroid level are actually numerical measures, the investigators transformed them into nominal variables by dividing the values into two categories.)
If the term independent variable is used to designate the group membership variables (eg, development of pulmonary embolism or not), or the X variable (eg, blood pressure measured by a finger device), and the term dependent is used to designate the variables whose means are compared (eg, pulse oximetry), or the Y variable (eg, blood pressure measured by the cuff device), the observations can be summarized as in Table 10–1. (For the sake of simplicity, this summary omits ordinal variables; variables measured on an ordinal scale are often treated as if they are nominal.) Data from several of the presenting problems are available on the CD-ROM [available only with the book], and we invite you to replicate the analyses as you go through this chapter.
| Independent Variable | Dependent Variable | Method |
|---|---|---|
| Nominal | Nominal | Chi-square |
| Nominal (binary) | Numerical | t testa |
| Nominal (more than two values) | Numerical | One-way |
| ANOVAa | ||
| Nominal | Numerica (censored) | Actuarial methods |
| Numerical | Numerical | Regressionb |
![]() Statistical techniques involving multiple variables are used increasingly in medical research, and several of them are illustrated in this chapter. The multiple-regression model, in which several independent variables are used to explain or predict the values of a single numerical response, is presented first, partly because it is a natural extension of the regression model for one independent variable illustrated in Chapter 8. More importantly, however, all the other advanced methods except meta-analysis can be viewed as modifications or extensions of the multiple-regression model. All except meta-analysis involve more than two observations per subject and are concerned with explanation or prediction.
Statistical techniques involving multiple variables are used increasingly in medical research, and several of them are illustrated in this chapter. The multiple-regression model, in which several independent variables are used to explain or predict the values of a single numerical response, is presented first, partly because it is a natural extension of the regression model for one independent variable illustrated in Chapter 8. More importantly, however, all the other advanced methods except meta-analysis can be viewed as modifications or extensions of the multiple-regression model. All except meta-analysis involve more than two observations per subject and are concerned with explanation or prediction.
![]() The goal in this chapter is to present the logic of the different methods listed in Table 10–2 and to illustrate how they are used and interpreted in medical research. These methods are generally not mentioned in traditional introductory texts, and most people who take statistics courses do not learn about them until their third or fourth course. These methods are being used more frequently in medicine, however, partly because of the increased involvement of statisticians in medical research and partly because of the availability of complex statistical computer programs. In truth, few of these methods would be used very much in any field were it not for computers because of the time-consuming and complicated computations involved. To read the literature with confidence, especially studies designed to identify prognostic or risk factors, a reasonable acquaintance with the methods described in this chapter is required. Few of the available elementary books discuss multivariate methods. One that is directed toward statisticians is nevertheless quite readable (Chatfield, 1995); Katz (1999) is intended for readers of the medical literature and contains explanations of many of topics we discuss in this chapter (Dawson, 2000), as does Norman and Streiner (1996).
The goal in this chapter is to present the logic of the different methods listed in Table 10–2 and to illustrate how they are used and interpreted in medical research. These methods are generally not mentioned in traditional introductory texts, and most people who take statistics courses do not learn about them until their third or fourth course. These methods are being used more frequently in medicine, however, partly because of the increased involvement of statisticians in medical research and partly because of the availability of complex statistical computer programs. In truth, few of these methods would be used very much in any field were it not for computers because of the time-consuming and complicated computations involved. To read the literature with confidence, especially studies designed to identify prognostic or risk factors, a reasonable acquaintance with the methods described in this chapter is required. Few of the available elementary books discuss multivariate methods. One that is directed toward statisticians is nevertheless quite readable (Chatfield, 1995); Katz (1999) is intended for readers of the medical literature and contains explanations of many of topics we discuss in this chapter (Dawson, 2000), as does Norman and Streiner (1996).
| Independent Variables | Dependent Variable | Method(s) |
|---|---|---|
| Nominal | Nominal | Log-linear |
| Nominal and numerical | Nominal (binary) | Logistic regression |
| Nominal and numerical | Nominal (2 or more categories) | Logistic regression |
| Discriminant analysisa | ||
| Cluster analysis | ||
| Propensity scores | ||
| CART | ||
| Nominal | Numerical | ANOVAa |
| MANOVAa | ||
| Numerical | Numerical | Multiple regressiona |
| Nominal and numerical | Numerical (censored) | Cox propotional hazard model |
| Confounding factors | Numerical | ANCOVAa |
| MANOVAa | ||
| GEEa | ||
| Confounding factors | Nominal | Mantel–Haenszel |
| Numerical only | Factor analysis |
![]() Before we examine the advanced methods, however, a comment on terminology is necessary. Some statisticians reserve the term “multivariate” to refer to situations that involve more than one dependent (or response) variable. By this strict definition, multiple regression and most of the other methods discussed in this chapter would not be classified as multivariate techniques. Other statisticians, ourselves included, use the term to refer to methods that examine the simultaneous effect of multiple independent variables. By this definition, all the techniques discussed in this chapter (with the possible exception of some meta-analyses) are classified as multivariate.
Before we examine the advanced methods, however, a comment on terminology is necessary. Some statisticians reserve the term “multivariate” to refer to situations that involve more than one dependent (or response) variable. By this strict definition, multiple regression and most of the other methods discussed in this chapter would not be classified as multivariate techniques. Other statisticians, ourselves included, use the term to refer to methods that examine the simultaneous effect of multiple independent variables. By this definition, all the techniques discussed in this chapter (with the possible exception of some meta-analyses) are classified as multivariate.
Multiple Regression
Simple linear regression (Chapter 8) is the method of choice when the research question is to predict the value of a response (dependent) variable, denoted Y, from an explanatory (independent) variable X. The regression model is
For simplicity of notation in this chapter we use Y to denote the dependent variable, even though Y′, the predicted value, is actually given by this equation. We also use a and b, the sample estimates, instead of the population parameters, β0 and β1, where a is the intercept and b the regression coefficient. Please refer to Chapter 8 if you’d like to review simple linear regression.
![]() The extension of simple regression to two or more independent variables is straightforward. For example, if four independent variables are being studied, the multiple regression model is
The extension of simple regression to two or more independent variables is straightforward. For example, if four independent variables are being studied, the multiple regression model is
where X1 is the first independent variable and b1 is the regression coefficient associated with it, X2 is the second independent variable and b2 is the regression coefficient associated with it, and so on. This arithmetic equation is called a linear combination; thus, the response variable Y can be expressed as a (linear) combination of the explanatory variables. Note that a linear combination is really just a weighted average that gives a single number (or index) after the X’s are multiplied by their associated b’s and the bX products are added. The formulas for a and b were given in Chapter 8, but we do not give the formulas in multiple regression because they become more complex as the number of independent variables increases; and no one calculates them by hand, in any case.
The dependent variable Y must be a numerical measure. The traditional multiple-regression model calls for the independent variables to be numerical measures as well; however, nominal independent variables may be used, as discussed in the next section. To summarize, the appropriate technique for numerical independent variables and a single numerical dependent variable is the multiple regression model, as indicated in Table 10–2.
Multiple regression can be difficult to interpret, and the results may not be replicable if the independent variables are highly correlated with each other. In the extreme situation, two variables that are perfectly correlated are said to be collinear. When multicollinearity occurs, the variances of the regression coefficients are large so the observed value may be far from the true value. Ridge regression is a technique for analyzing multiple regression data that suffer from multicollinearity by reducing the size of standard errors. It is hoped that the net effect will be to give more reliable estimates. Another regression technique, principal components regression, is also available, but ridge regression is the more popular of the two methods.
Jackson and colleagues (2002) (Presenting Problem 1) wanted to study the way in which sex, age, and race affect the relationship between BMI and percent body fat. We provide some basic information on these variables in Table 10–3 and see the study included 121 black females, 238 white females, 81 black men, and 215 white men.
| Report | |||||
|---|---|---|---|---|---|
| Gender | Race 2 | Age | BMI | PCTFAT | |
| Female | Black | Mean | 32.7770 | 28.1380 | 35.997 |
| N | 121 | 121 | 121 | ||
| Standard deviation | 11.35229 | 6.14086 | 8.756 | ||
| White | Mean | 34.4032 | 24.8182 | 29.971 | |
| N | 238 | 238 | 238 | ||
| Standard deviation | 13.79910 | 4.91353 | 9.8447 | ||
| Total | Mean | 33.8551 | 25.9371 | 32.002 | |
| N | 359 | 359 | 359 | ||
| Standard deviation | 13.03256 | 5.57608 | 9.9349 | ||
| Male | Black | Mean | 34.2526 | 26.9269 | 22.944 |
| N | 81 | 81 | 81 | ||
| Standard deviation | 11.97843 | 4.83454 | 7.3195 | ||
| White | Mean | 36.4834 | 26.5334 | 22.963 | |
| N | 215 | 215 | 215 | ||
| Standard deviation | 15.06562 | 4.66455 | 9.0302 | ||
| Total | Mean | 35.8730 | 26.6411 | 22.958 | |
| N | 296 | 296 | 296 | ||
| Standard deviation | 14.30226 | 4.70670 | 8.5839 | ||
| Total | Black | Mean | 33.3687 | 27.6524 | 30.763 |
| N | 202 | 202 | 202 | ||
| Standard deviation | 11.60057 | 5.67188 | 10.4632 | ||
| White | Mean | 35.3905 | 25.6322 | 26.645 | |
| N | 453 | 453 | 453 | ||
| Standard deviation | 14.43550 | 4.86781 | 10.0846 | ||
| Total | Mean | 34.7670 | 26.2552 | 27.915 | |
| N | 655 | 655 | 655 | ||
| Standard deviation | 13.64747 | 5.20919 | 10.3710 | ||
![]() Table 10–4 shows the regression equation to predict percent body fat (see the bold values). Focusing initially on the Regression Equation Section, we see that all the variables are statistically significantly related to percent body fat.
Table 10–4 shows the regression equation to predict percent body fat (see the bold values). Focusing initially on the Regression Equation Section, we see that all the variables are statistically significantly related to percent body fat.
| Multiple Regression Report | |||
|---|---|---|---|
| Run Summary Section | |||
| Parameter | Value | Parameter | Value |
| Dependent variable | PCTFAT | Rows processed | 655 |
| Number independent variables | 4 | Rows filtered out | 0 |
| Weight variable | None | Rows with X’s missing | 0 |
| R2 | 0.8042 | Rows with weight missing | 0 |
| Adj R2 | 0.8030 | Rows with Y missing | 0 |
| Coefficient of variation | 0.1649 | Rows used in estimation | 655 |
| Mean square error | 21.18832 | Sum of weights | 655.000 |
| Square root of MSE | 4.603077 | Completion status | Normal completion |
| Ave Abs Pct Error | 19.089 | ||
The first variable is a numerical variable, age, with regression coefficient, b, of 0.1603, indicating that greater age is associated with higher percent body fat. The second variable, BMI, is also numerical; the regression coefficient of 1.3710 indicates that patients with higher BMI also have higher percent body fat, which certainly makes sense.
![]() The third variable, sex, is a binary variable having two values. For regression models it is convenient to code binary variables as 0 and 1; in the Jackson example, females have a 0 code for sex, and males have a 1. This procedure, called dummy or indicator coding, allows investigators to include nominal variables in a regression equation in a straightforward manner. The dummy variables are interpreted as follows: A subject who is male has the code for males, 1, multiplied by the regression coefficient for sex, 1.3710, resulting in an additional 1.3710 points being added to his percent body fat. The decision of which value is assigned 1 and which is assigned 0 is an arbitrary decision made by the researcher but can be chosen to facilitate interpretations of interest to the researcher.
The third variable, sex, is a binary variable having two values. For regression models it is convenient to code binary variables as 0 and 1; in the Jackson example, females have a 0 code for sex, and males have a 1. This procedure, called dummy or indicator coding, allows investigators to include nominal variables in a regression equation in a straightforward manner. The dummy variables are interpreted as follows: A subject who is male has the code for males, 1, multiplied by the regression coefficient for sex, 1.3710, resulting in an additional 1.3710 points being added to his percent body fat. The decision of which value is assigned 1 and which is assigned 0 is an arbitrary decision made by the researcher but can be chosen to facilitate interpretations of interest to the researcher.
The final variable is race, also dummy coded, with 0 for black and 1 for white. The regression coefficient is negative and indicates that white patients have 0.9161 subtracted from their percent body fat. The intercept itself is –8.3748, meaning that the predicted percent body fat is reduced by this amount after including all variables in the equation. The regression coefficients can be used to predict percent body fat by multiplying a given patient’s value for each independent variable X by the corresponding regression coefficient b and then summing to obtain the predicted percent body fat.
![]() Regression coefficients are interpreted differently in multiple regression than in simple regression. In simple regression, the regression coefficient b indicates the amount the predicted value of Y changes each time X increases by 1 unit. In multiple regression, a given regression coefficient indicates how much the predicted value of Y changes each time X increases by 1 unit, holding the values of all other variables in the regression equation constant—as though all subjects had the same value on the other variables. For example, predicted percent body fat is increased by 0.1603 for increase of 1 year in patient, assuming all other variables are held constant. This feature of multiple regression makes it an ideal method to control for baseline differences and confounding variables, as we discuss in the section titled “Controlling for Confounding.”
Regression coefficients are interpreted differently in multiple regression than in simple regression. In simple regression, the regression coefficient b indicates the amount the predicted value of Y changes each time X increases by 1 unit. In multiple regression, a given regression coefficient indicates how much the predicted value of Y changes each time X increases by 1 unit, holding the values of all other variables in the regression equation constant—as though all subjects had the same value on the other variables. For example, predicted percent body fat is increased by 0.1603 for increase of 1 year in patient, assuming all other variables are held constant. This feature of multiple regression makes it an ideal method to control for baseline differences and confounding variables, as we discuss in the section titled “Controlling for Confounding.”
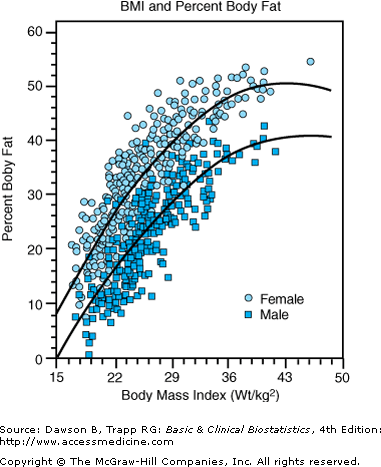
![]() It bears repeating that multiple regression measures only the linear relationship between the independent variables and the dependent variable, just as in simple regression. In the Jackson study, the authors examined the scatterplot between BMI and percent body fat, which we have reproduced in Figure 10–1. The figure indicates a curvilinear relationship, and investigators decided to transform BMI by taking its natural logarithm. They developed four models for females and males separately to examine the cumulative effect of including variables in the regression equation; results are reproduced in Table 10–5. Model I includes only ln BMI and the intercept; model II adds in the age, model III the race, and model IV interactions between ln BMI with race and age. The rationale for including interactions is the same as discussed in Chapter 7, namely that they wanted to know whether the relationship between ln BMI and percent body weight was the same for all levels of race or age.
It bears repeating that multiple regression measures only the linear relationship between the independent variables and the dependent variable, just as in simple regression. In the Jackson study, the authors examined the scatterplot between BMI and percent body fat, which we have reproduced in Figure 10–1. The figure indicates a curvilinear relationship, and investigators decided to transform BMI by taking its natural logarithm. They developed four models for females and males separately to examine the cumulative effect of including variables in the regression equation; results are reproduced in Table 10–5. Model I includes only ln BMI and the intercept; model II adds in the age, model III the race, and model IV interactions between ln BMI with race and age. The rationale for including interactions is the same as discussed in Chapter 7, namely that they wanted to know whether the relationship between ln BMI and percent body weight was the same for all levels of race or age.
| Female Models | Male Models | |||||||
|---|---|---|---|---|---|---|---|---|
| Variable | I | II | III | IV | I | II | III | IV |
| Intercept | 107.22a | 102.01a | 97.11a | 82.83a | 111.13a | 103.94a | 104.21a | 149.24a |
| In BMI | 43.05a | 39.96a | 38.67a | 34.43a | 41.04a | 37.31a | 37.35a | 51.31a |
| Age | 0.14a | 0.15a | 0.14a | 0.14a | 0.14a | 1.47a | ||
| Raceb | –1.63a | –26.02a | –0.23 | |||||
| Race x In BMI | 7.48a | |||||||
| Age x ln BMI | –0.41a | |||||||
| r2 | 0.78a | 0.80 | 0.81a | 0.82a | 0.67a | 0.72a | 0.72a | 0.73a |
| r2Δ | 0.01a | 0.01a | 0.01a | 0.05a | 0.00 | 0.01a | ||
| s.e.e. (% fat) | 4.7 | 4.4 | 4.3 | 4.3 | 4.9 | 4.6 | 4.6 | 4.5 |
Figure 10–1.
Plot illustrating the nonlinear relationship between BMI and percent body fat. (Data, used with permission, from Jackson AS, Stanforth PR, Gagnon J, Rankinen T, Leon AS, Rao DC, et al: The effect of sex, age, and race on estimating percentage body fat from body mass index: The Heritage Family Study. Int J Obes Relat Metab Disord 2002;26:789–796. Analysis produced using NCSS; used with permission.)
Table 10–6 shows the output from NCSS for model III for female subjects; it contains a number of features to discuss. In the upper half of the table, note the columns headed by t value and probability level. Both the t test and the F test can be used to determine whether a regression coefficient is different from zero, or the t distribution can be used to form confidence intervals for each regression coefficient. Remember that even though the P values are sometimes reported as 0.000, there is always some probability, even if it is very small. Many statisticians believe, and we agree, that it is more accurate to report P < 0.001.
| Regression Equation Section | ||||||
|---|---|---|---|---|---|---|
| Independent Variable | Regression Coefficient b(i) | Standard Error Sb(i) | T-Value to test H0:B(i)=0 | Prob Level | Reject H0 at 5%? | Power of Test at 5% |
| Intercept | –97.1096 | 4.0314 | –24.088 | 0.0000 | Yes | 1.0000 |
| Log_BMI | 38.6724 | 1.2684 | 30.490 | 0.0000 | Yes | 1.0000 |
| Age | 0.1510 | 0.0190 | 7.938 | 0.0000 | Yes | 1.0000 |
| Race | –1.6308 | 0.5125 | –3.182 | 0.0016 | Yes | 0.8875 |
Most authors present regression coefficients that can be used with individual subjects to obtain predicted Y values. But the size of the regression coefficients cannot be used to decide which independent variables are the most important, because their size is also related to the scale on which the variables are measured, just as in simple regression. For example, in Jackson and colleagues’ study, the variable race was coded 1 if white and 0 if black, and the variable age was coded as the number of years of age at the time of the first data collection. Then, if race and age are equally important in predicting subsequent depression, the regression coefficient for race would be much larger than the regression coefficient for age so that the same amount would be added to the prediction of percent body weight. These regression coefficients are sometimes called unstandardized; they cannot be used to draw conclusions about the importance of the variable, but only whether the relationship or with the dependent variable Y is positive or negative.a One way to eliminate the effect of scale is to standardize the regression coefficients. Standardization can be done by subtracting the mean value of X and dividing by the standard deviation before analysis, so that all variables have a mean of 0 and a standard deviation of 1. Then it is possible to compare the magnitudes of the regression coefficients and draw conclusions about which explanatory variables play an important role. It is also possible to calculate the standardized regression coefficients after the regression model has been developed.b The larger the standardized coefficient, the larger the value of the t statistic. Standardized regression coefficients are often referred to as beta (β) coefficients. The major disadvantage of standardized regression coefficients is that they cannot readily be used to predict outcome values. The lower half of Table 10–6 contains the standardized regression coefficients in the far right column for the variables used to percent body fat in Jackson and colleagues’ study. Using the standardized coefficients in Table 10–6, can you determine which variable, age or race, has more influence in predicting subsequent depression? If you chose age, you are correct, because the absolute value of its standardized coefficient is larger, 0.1981, compared with –0.0777 for race.
aTechnically it is possible for the regression coefficient and the correlation to have different signs. If so, the variable is called a moderator variable; it affects the relationship between the dependent variable and another independent variable.
bThe standardized coefficient = the unstandardized coefficient multiplied by the standard deviation of the X variable and divided by the standard deviation of the Y variable: βj = bj (SDX/SDY).
![]() Multiple R is the multiple-regression analogue of the Pearson product moment correlation coefficient r. It is also called the coefficient of multiple determination, but most authors use the shorter term. As an example, suppose percent body fat is calculated for each person in the study by Jackson and colleagues; then, the correlation between predicted percent body fat and the actual percent body fat is calculated. This correlation is the multiple R. If the multiple R is squared (R2), it measures how much of the variation in the actual depression score is accounted for by knowing the information included in the regression equation. The term R2 is interpreted in exactly the same way as r2 in simple correlation and regression, with 0 indicating no variance accounted for and 1.00 indicating 100% of the variance accounted for. Recall that in simple regression, the correlation between the actual value Y of the dependent variable and the predicted value, denoted Y′, is the same as the correlation between the dependent variable and the independent variable; that is, rY′Y = rXY. Thus, R and R2 in multiple regression play the same role as r and r2 in simple regression. The statistical test for R and R2, however, uses the F distribution instead of the t distribution.
Multiple R is the multiple-regression analogue of the Pearson product moment correlation coefficient r. It is also called the coefficient of multiple determination, but most authors use the shorter term. As an example, suppose percent body fat is calculated for each person in the study by Jackson and colleagues; then, the correlation between predicted percent body fat and the actual percent body fat is calculated. This correlation is the multiple R. If the multiple R is squared (R2), it measures how much of the variation in the actual depression score is accounted for by knowing the information included in the regression equation. The term R2 is interpreted in exactly the same way as r2 in simple correlation and regression, with 0 indicating no variance accounted for and 1.00 indicating 100% of the variance accounted for. Recall that in simple regression, the correlation between the actual value Y of the dependent variable and the predicted value, denoted Y′, is the same as the correlation between the dependent variable and the independent variable; that is, rY′Y = rXY. Thus, R and R2 in multiple regression play the same role as r and r2 in simple regression. The statistical test for R and R2, however, uses the F distribution instead of the t distribution.
The computations are time-consuming, and fortunately, computers do them for us. Jackson and colleagues included R2 in Table 10–5 (although they used lowercase r2); it was 0.81 for model III (and is also shown in the NCSS output in Table 10–4). After ln BMI, age, and race are entered into the regression equation, R2 = 0.81 indicates that more than 80% of the variability in percent body fat is accounted for by knowing patients’ BMI, age, and race. Because R2 is less than 1, we know that factors other than those included in the study also play a role in determining a person’s percent body fat.
![]() The primary purpose of Jackson and colleagues in their study of BMI and percent body fat was explanation; they used multiple regression analysis to learn how specific characteristics confounded the relationship between BMI and percent body fat. They also wanted to know how the characteristics interacted with one another, such as gender and race. Some research questions, however, focus on the prediction of the outcome, such as using the regression equation to predict of percent body fat in future subjects.
The primary purpose of Jackson and colleagues in their study of BMI and percent body fat was explanation; they used multiple regression analysis to learn how specific characteristics confounded the relationship between BMI and percent body fat. They also wanted to know how the characteristics interacted with one another, such as gender and race. Some research questions, however, focus on the prediction of the outcome, such as using the regression equation to predict of percent body fat in future subjects.
Deciding on the variables that provide the best prediction is a process sometimes referred to as model building and is exemplified in Table 10–5. Selecting the variables for regression models can be accomplished in several ways. In one approach, all variables are introduced into the regression equation, called the “enter” method in SPSS and used in the multiple regression procedure in NCSS. Then, especially if the purpose is prediction, the variables that do not have significant regression coefficients are eliminated from the equation. The regression equation may be recalculated using only the variables retained because the regression coefficients have different values when some variables are removed from the analysis.
Computer programs also contain routines to select an optimal set of explanatory variables. One such procedure is called forward selection. Forward selection begins with one variable in the regression equation; then, additional variables are added one at a time until all statistically significant variables are included in the equation. The first variable in the regression equation is the X variable that has the highest correlation with the response variable Y. The next X variable considered for the regression equation is the one that increases R2 by the largest amount. If the increment in R2 is statistically significant by the F test, it is included in the regression equation. This step-by-step procedure continues until no X variables remain that produce a significant increase in R2. The values for the regression coefficients are calculated, and the regression equation resulting from this forward selection procedure can be used to predict outcomes for future subjects. The increment in R2 was calculated by Jackson and colleagues; it is shown as r2Δ in Table 10–5.
A similar backward elimination procedure can also be used; in it, all variables are initially included in the regression equation. The X variable that would reduce R2 by the smallest increment is removed from the equation. If the resulting decrease is not statistically significant, that variable is permanently removed from the equation. Next, the remaining X variables are examined to see which produces the next smallest decrease in R2. This procedure continues until the removal of an X variable from the regression equation causes a significant reduction in R2. That X variable is retained in the equation, and the regression coefficients are calculated.
When features of both the forward selection and the backward elimination procedures are used together, the method is called stepwise regression (stepwise selection). Stepwise selection is commonly used in the medical literature; it begins in the same manner as forward selection. After each addition of a new X variable to the equation, however, all previously entered X variables are checked to see whether they maintain their level of significance. Previously entered X variables are retained in the regression equation only if their removal would cause a significant reduction in R2. The forward versus backward versus stepwise procedures have subtle advantages related to the correlations among the independent variables that cannot be covered in this text. They do not generally produce identical regression equations, but conceptually, all approaches determine a “parsimonious” equation using a subset of explanatory variables.
Some statistical programs examine all possible combinations of predictor values and determine the one that produces the overall highest R2, such as All Possible Regression in NCSS. We do not recommend this procedure, however, and suggest that a more appealing approach is to build a model in a logical way. Variables are sometimes grouped according to their function, such as all demographic characteristics, and added to the regression equation as a group or block; this process is often called hierarchical regression; see exercise 7 for an example. The advantage of a logical approach to building a regression model is that, in general, the results tend to be more stable and reliable and are more likely to be replicated in similar studies.
![]() Polynomial regression is a special case of multiple regression in which each term in the equation is a power of X. Polynomial regression provides a way to fit a regression model to curvilinear relationships and is an alternative to transforming the data to a linear scale. For example, the following equation can be used to predict a quadratic relationship:
Polynomial regression is a special case of multiple regression in which each term in the equation is a power of X. Polynomial regression provides a way to fit a regression model to curvilinear relationships and is an alternative to transforming the data to a linear scale. For example, the following equation can be used to predict a quadratic relationship:
If a linear and cubic term do not provide an adequate fit, a cubic term, a fourth-power term, and so on, can also be included until an adequate fit is obtained.
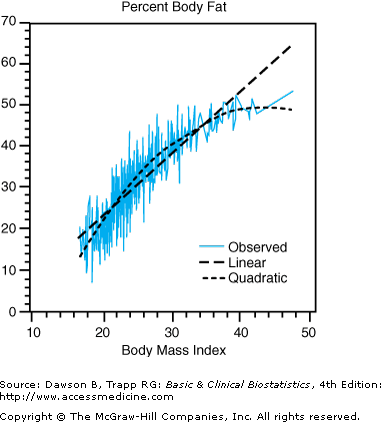
Jackson and colleagues (2002) used polynomial regression to fit separate curves for men and women, illustrated in Figure 10–1. Two approaches to polynomial regression can be used. The first method calculates squared terms, cubic terms, and so on; these terms are then entered one at a time using multiple regression. Another approach is to use a program that permits curve fitting, such as the regression curve estimation procedure in SPSS. We used the SPSS procedure to fit a quadratic curve of BMI to percent body fat for women. The regression equation was:
A plot is produced by SPSS is given in Figure 10–2.