BIOSTATISTICS

Lawrence A. Frazee, PharmD, BCPS, and Mate M. Soric, PharmD, BCPS

CASE

A new antihypertensive agent, appesartan, has been tested in a large randomized, double-blind, placebo-controlled trial consisting of patients at high risk for myocardial infarction. The primary endpoint was cardiovascular death. F.M. has been asked to review the literature supporting the use of appesartan and is having difficulty understanding the statistics involved in the trial.

WHY IT’S ESSENTIAL

The practice of evidence-based medicine depends on the interpretation and application of the results of clinical trials. Without empirical evidence from well-designed clinical trials, decisions about whether a therapy is safe and effective can be made based only on anecdotal experience. Biostatistics is the mathematical science that describes observations made during experimentation, helps us to decide whether observed differences are likely to be real, and allows us to describe the magnitude of benefit and harm so that rational therapy decisions can be made. It is important for you to have a basic understanding of biostatistics when evaluating medical literature throughout the APPE rotations and beyond.

SUMMARIZING DATA

Before any statistical test can be performed, the aggregate data from any trial must be summarized. Being able to describe the data allows you to choose the appropriate statistical test and report results in an easy-to-understand way.

Types of Data

In general, outcome data are described as categorical, ordinal, or continuous. Categorical variables with only two possible categories are referred to as binomial data. Sex is an example of a binomial variable, and mortality is an example of a binomial outcome. A categorical variable with more than two possible outcomes (such as race or ethnicity) is a nominal variable. In either case, a categorical variable has no inherent order.

QUICK TIP

Being able to identify the type of data in a trial is vital to ensuring the proper statistical tests are used for analysis.

Ordinal variables have an inherent order, but the specific number has no mathematical meaning. A common example is a 10-point pain scale in which a score of 10 is higher than a score of 9. With this type of data, however, the differences between two numbers on the scale are not necessarily equal, meaning the difference between a 1 and 2 may not be the same as the difference between a 9 and 10.

Continuous data are data that come in the form of any numerical value (as opposed to discrete categories). This category is further subdivided into interval and ratio data. Temperature on the Celsius scale is an example of an interval variable because a difference of 1°C has the same meaning along the entire scale but the definition of zero is arbitrary. Because of this, a ratio cannot be calculated to express the relationship between outcomes measured on a continuous interval scale. Because 0°C does not mean “no temperature,” one cannot say that 50°C is twice as much temperature as 25°C. Conversely, a continuous variable that is measured on a scale with a nonarbitrary value of zero is a ratio variable. The Kelvin scale for measuring temperature is an example of a continuous ratio scale because it contains an absolute zero value. Mass is also an example of a ratio variable because a value of 0 grams does, indeed, mean no mass. Outcomes on this scale can be expressed as a ratio because 50 grams is twice as much mass as 25 grams.

CASE QUESTION

Categorize each of the following variables from the appesartan trial as a binomial, nominal, ordinal, interval, or ratio variable: concomitant use of a beta-blocker, blood pressure reduction, quality-of-life score based on a Likert scale, cardiac survival, recruitment site.

Sometimes data collected on an ordinal or continuous scale can be expressed in a categorical way. For example, a placebo-controlled trial of a new diabetes medicine could present the average change in hemoglobin A1c from baseline with the new medicine compared with placebo. If the average change in hemoglobin A1c with the new medicine was –2.3 points, we know that some patients achieved a greater reduction while some achieved a smaller one. But what if the investigators are not interested in the average change in hemoglobin A1c as much as how many subjects reach the goal hemoglobin A1c of 7%? The study could be designed to report the proportion of patients who reach their goal with the new medicine compared to placebo, thus presenting continuous data on a categorical scale. In fact, most large comparative clinical trials measure outcomes on a categorical scale.

CASE QUESTION

One of the secondary endpoints in the appesartan trial is reduction in systolic blood pressure. How could this continuous outcome be converted into a categorical outcome?

Descriptive Statistics

Before a statistical test can be performed, descriptive statistics must be used to summarize the central tendency of the data. For categorical data, the most straightforward descriptive statistic is the proportion of subjects that fall into each category. When the scale has only two categories (yes or no), there is usually only one proportion reported. For example, a study that has mortality as an outcome will report the proportion of patients in each group that died because this is a binomial outcome (patients either died or survived).

For ordinal and continuous data, an expression of central tendency is needed to describe the outcome. The mean (average) has the advantage of being well suited for mathematical manipulation but is also easily influenced by outliers if the data are not normally distributed. The median, on the other hand, is the value for which half of the data points are below and half are above. The median has the advantage of not being as influenced by outliers but is not as easy to manipulate mathematically. Lastly, the mode is the value that occurs most often in a data set.

The mean is the most common and useful expression of central tendency for continuous data. There are, however, circumstances when the mean may not be appropriate, especially if the data are not normally distributed. It is not uncommon for studies to report the length of hospital stay as a median rather than a mean due to outliers that could skew the results. For ordinal data, such as a pain scale, the median is the most appropriate expression of central tendency, although it is not uncommon to see these outcomes expressed as a mean.

ESTABLISHING STATISTICAL SIGNIFICANCE

Two processes limit our ability to draw conclusions from clinical trials—bias and chance. Bias is a systematic error that tends to skew results in one particular and predictable direction, whereas chance is, by definition, a random process. There are several types of bias to be aware of when evaluating the literature, but one of the more common types is selection bias. Most common in observational studies, selection bias occurs when patients end up in a particular group based on something other than the variable being studied. An example might be an observational study designed to assess the incidence of tachycardia in patients with acute asthma treated with one of two different beta agonists. If prescribers are more likely to select one particular beta agonist in patients who present with baseline tachycardia (perhaps because of a belief that it causes fewer beta-mediated side effects), it will be difficult to determine whether any observed difference in heart rate after treatment is due to treatment selection or patient selection. Performing statistical tests on the results of a strongly biased clinical trial will do nothing to eliminate bias. If a trial is biased to produce results in one direction, it is likely that our statistical tests will demonstrate statistical difference in that direction because there is a true difference between the groups. The problem is that the difference observed is likely due to something other than the variable under study. The primary method to minimize bias is through rigorous trial design. Prospective randomized group assignment and blinding are two of the most common methodologies employed in this regard.

QUICK TIP

Although clinicians must always be on the lookout for bias, the potential for bias does not necessarily mean that it is present, nor does it mean that the bias is actually skewing the results to a significant degree.

Despite our best efforts at selecting a study population and assigning individuals to treatment groups in an unbiased way, there is still a possibility that the group will differ from the population as a whole. This is often referred to as random sampling error and is due to chance. There are two general approaches used to assess the effect of chance on observed outcomes. The first approach is called hypothesis testing and produces the well-known “P value.” The second approach is called estimation and is represented by the point estimate and confidence interval.

CASE QUESTION

F.M. has noted that, despite the randomized trial design, the two groups used in the appesartan trial were significantly different with regard to smoking status. What type of error has been identified?

Hypothesis Testing

The proper statistical test allows the clinician to determine with a certain level of confidence whether the observed difference between groups is real or due to random chance. Before we get into the specifics of hypothesis testing, it is important to understand some of the assumptions that underlie statistical testing in biomedical research. Perhaps the best way to understand this is with an example from jurisprudence.

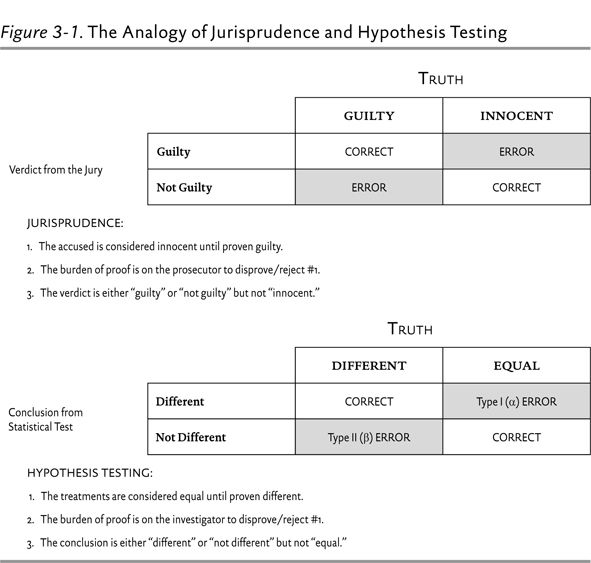
The phrases “innocent until proven guilty” and that guilt must be proven “beyond a reasonable doubt” are most likely familiar to anyone who has seen an episode of Law and Order. Where do such phrases come from, and how do they relate to statistical testing? In the American legal system, when a person is accused of a crime, the accused is assumed to be innocent and the prosecutor must prove that he or she is guilty. If the prosecutor is not able to do this, then the defendant cannot be found guilty. The assumption of innocence is intentional because it is borne out of a culture that values freedom. No system will come to the true conclusion 100% of the time, so it must be asked if it is better to convict an innocent person or to acquit a guilty person. Because we place a high value on freedom, the American legal system is designed so that the burden of proof is on the prosecutor. If the amount and magnitude of the evidence is enough to prove the defendant guilty beyond a reasonable doubt, then the jury will return a verdict of “guilty.” If there is reasonable doubt regarding the guilt of the defendant, the jury will return a verdict of “not guilty.” Notice that in this system, either the defendant is guilty or the jury is unable to say that the defendant is guilty. The jury cannot say that he or she is innocent.

This example is very instructive for understanding hypothesis testing. Biomedical researchers want to be as sure as possible that a treatment is truly effective. They would rather take the chance of saying that an effective treatment is not effective than say that an ineffective treatment is effective. The assumption is that there is no difference in the outcome under study between the study treatment group and the control group (innocent until proven guilty). The burden of proof is on the investigator to prove that the study treatment is more effective than the comparator. If the statistical test shows that the difference between groups is real beyond a reasonable doubt, the investigator will conclude that the treatments are statistically different. If this cannot be shown beyond a reasonable doubt, the investigator must conclude that they are not different. In a classic superiority trial, where the study treatment is compared to placebo or standard treatment, this is accomplished by attempting to disprove the null hypothesis (H₀). The null hypothesis posits that there is no difference in the outcome being studied between groups. If the outcome is mortality and two treatments (A and B) are being compared, then the null hypothesis would be that mortality in treatment group A is equal to mortality in treatment group B. The study is then designed with the goal of disproving, or rejecting, the null hypothesis. This is analogous to assuming that the defendant is innocent and then going to trial to try to disprove or reject this hypothesis. Figure 3-1 illustrates the comparison between hypothesis testing and jurisprudence.

Avoiding Error

Type I Error

As shown in Figure 3-1, there are four possible conclusions in hypothesis testing, two of them correct and two of them incorrect. A type I error is made when a statistical test concludes that two treatments are different when there really is no difference—analogous to convicting an innocent person. The probability of making a type I error is given by the P value.

Let’s consider the example of a study that compared the beta-blocker bisoprolol to placebo to reduce postoperative 30-day mortality in high-risk patients undergoing noncardiac vascular surgery.¹ Investigators reported that the incidence of cardiac death at 30 days was 3.4% in the bisoprolol group and 17% in the placebo group, with a reported P value of 0.02. The absolute treatment difference between groups is 13.6% (17 minus 3.4), but what is the likelihood that this difference is real and not due to selecting higher-risk patients in the placebo group by random chance? The answer is the P value.

The null hypothesis in this study was that the 30-day mortality would be the same in the bisoprolol and placebo groups, resulting in an absolute treatment difference of zero. The P value represents a 2% probability that the mortality difference observed (13.6%) would have been obtained when the null hypothesis (mortality difference of 0%) was, in fact, true. In other words, there is a 2% chance that a type I error was made. In biomedical research, we are willing to accept up to a 5% probability of making a type I error, although this is a completely arbitrary value.

CASE QUESTION

Patients who used appesartan had a mortality rate of 80 out of 1,000 (8%), compared with 100 out of 1,000 (10%) in the placebo group. The corresponding

Stay updated, free articles. Join our Telegram channel

Join