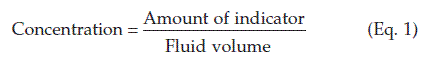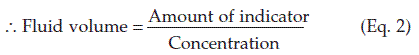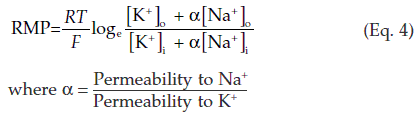Chapter 1 Basic principles and cell physiology
The physiology of the body is often described in terms of the homeostatic mechanisms which control the cellular environment. Cell function also relies on an adequate energy supply and the appropriate integration of the activities of the different cells within the body through efficient signalling mechanisms, both electrical and chemical. The cell membrane is very important in many of these functions since it forms a barrier between the intracellular and extracellular environments across which important molecules must be transported. The properties of the membranes of excitable cells also account for the generation of action potentials, and many of the receptors which recognize specific chemical messengers are membrane bound.
1.1 Cells, systems and homeostasis
At the end of this section you should be able to:
Cell structure
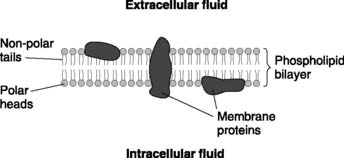
Although cells from different organs show considerable differences in shape (morphology) and function, all cells share some general characteristics. Each is bounded by a cell membrane (or plasma membrane) which separates the aqueous solution inside the cell (the cytoplasm or intracellular fluid) from the aqueous solution outside (the extracellular fluid). These two fluids have very different ionic compositions (see Section 5.1) and these differences are more easily maintained because ions cannot readily cross the double layer (bilayer) of phospholipids in the plasma membrane (Fig. 1). These are oriented with their hydrophilic heads adjacent to the aqueous solutions on either side, while their hydrophobic tails form a fatty core. Membrane proteins move about within the two-dimensional confines of the lipid layer (the fluid mosaic model of the membrane).
Membranes also delimit a number of subcellular units known as organelles. These include:
Body fluid compartments
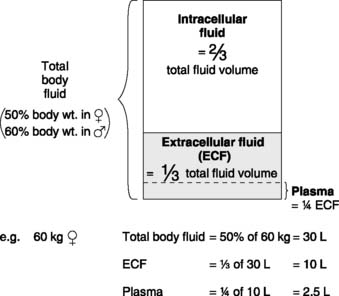
The body contains many different aqueous solutions, which may be classified into a series of fluid compartments depending on their location (Fig. 2). The main subdivision is between intracellular and extracellular fluids. The extracellular compartment represents all fluid not inside cells, including the plasma component of blood, aqueous humour in the eye, synovial fluid in joints and cerebrospinal fluid within the central nervous system. The largest single extracellular subcompartment, however, consists of the interstitial fluid, which lies in the connective tissue matrix surrounding most body cells. It is normally this fluid which is in direct contact with the cell membrane and controlling interstitial conditions is vital for normal cell function. Much of this control is achieved by the continuous circulation of blood through the cardiovascular system. The rate of blood flow to any region and the plasma concentrations of different solutes greatly influence the cellular environment since, with the exception of plasma proteins, water and solutes move freely between plasma and the interstitium.
Volume measurement by indicator (dye) dilution methods
The volume of a given fluid compartment, e.g., the extracellular fluid volume, is usually estimated indirectly using an indicator substance. If a known quantity of indicator becomes evenly distributed through that compartment, measurement of the final concentration of indicator allows the volume of fluid to be calculated using Equation 2 below.
For these reasons different indicators are appropriate when estimating the volume of different fluid spaces within the body.
Extracellular fluid volume
Extracellular fluid volume is not easily measured and different indicators give different results in a given subject. Substances which have been used include radioactive sodium, radioactive bromide, the polysaccharide inulin, and sucrose. Mean values are about 10–15 L. The plasma volume represents about 25% of the extracellular space and, since there is free exchange of fluid across the capillary wall, any increase or decrease in extracellular fluid volume will be reflected by a parallel change in plasma volume. This means that mechanisms which affect the total extracellular fluid volume will also alter the plasma and, therefore, blood volumes, e.g., renal fluid reabsorption (Section 5.4).
Homeostasis
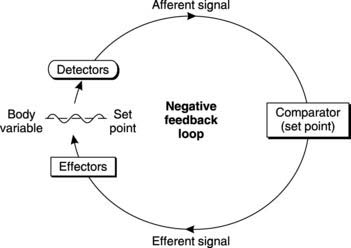
The following general elements are present in all homeostatic control systems (Fig. 3).
In such a system, any deviation of the variable away from its normal (set) value stimulates responses which reduce that deviation. This is referred to as negative feedback control and is an important element of homeostasis. The overall effect is to maintain a constant environment but often a phenomenon known as hunting is observed in which the controlled variable oscillates around a fixed mean value rather than remaining exactly at the set point (Fig. 3).
Homeostatic regulation of body temperature
Temperature detectors (thermoreceptors) monitor both the core temperature (the regulated variable) and the peripheral temperature (a separate but relevant variable). The afferent inputs go to an integrating centre (the thermoregulatory centre) in the hypothalamus of the brain, which compares core temperature with the set point of 37°C. If these differ, outgoing nerve signals activate a number of effector systems which alter the rates of heat production and heat loss.
In hot conditions the rate of heat loss can be greatly accelerated by:
1 2 Energy sources in the cell
Body cells require energy to carry out mechanical work (e.g., in muscle cells), to transport ions or molecules against concentration gradients (e.g., ion pumps) and for the synthesis of complex molecules. These active processes are ultimately fuelled by the energy released through the breakdown of carbohydrate, fat and protein from our diet. The initial series of reactions in the breakdown of glucose is referred to as glycolysis and does not require O2 (anaerobic metabolism). This leads to the formation of lactic acid and produces small amounts of adenosine triphosphate (ATP), the main source of usable energy within the cell. In the presence of O2 (aerobic conditions), however, intramitochondrial enzymes catalyse the complete catabolism of the products of glycolysis, releasing much greater amounts of ATP and generating CO2 and water as byproducts (Section 4.7). Whereas glycolysis leads to a net production of two molecules of ATP per glucose molecule, oxidative metabolism can produce an additional 34–36 ATP molecules. Subsequent hydrolysis of the high-energy phosphate bonds in ATP by ATPase enzymes makes energy available for the active processes of the cell.
1.3 Transport across cell membranes
At the end of this section you should be able to:
There is a constant traffic across cell membranes, supplying O2 and substrate molecules for intracellular metabolism and removing CO2, waste substances and active products. A variety of transport mechanisms are involved.
Diffusion
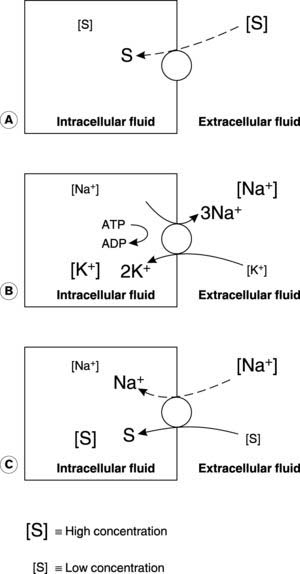
Membrane permeability to the solute. The plasma membrane is selectively permeable to fatty and small nonpolar molecules which dissolve in the membrane lipid. Thus, fatty acids, steroid hormones, O2 and CO2 all diffuse readily into cells. The permeability to water-soluble (lipid-insoluble) ions and large polar molecules such as proteins, however, is generally low. Certain ions can diffuse across the cell membrane much more readily (i.e., they are more permeant) than their lipid solubility would predict. This is because of membrane proteins which bridge the lipid barrier and provide an easier route for ion diffusion. These may take the form of carrier molecules, which bind to the ion and then move it across the membrane by changing conformation, or they may provide fluid-filled channels through which the ions can pass (Section 1.4). The roles of both these types of molecule are considered in more detail later in the chapter. Specific carriers and channels are selective for different kinds of ion and so membrane permeability to a given ion may differ widely from cell to cell, depending on which proteins are present.
Molecular weight of the diffusing substance. Small molecules diffuse more rapidly.
Osmosis
The osmotic properties of a solution can be described in several ways.
Tonicity is a biological term relating to the actual effect of a solution on living cells, specifically erythrocytes. A solution may be:
Carrier-mediated transport
Carrier proteins in the cell membrane bind to a specific substrate and then undergo some conformational change. As a result, the substrate is transported across the membrane and released on the other side. The rate of transport increases as the substrate concentration increases, but the maximum rate of transport (Vmax) is dependent on the density of carriers in a given cell, since all transport sites will be occupied above a certain substrate concentration (Fig. 4). This is referred to as saturation. Substrate specificity and saturation are two hallmarks of carrier-mediated transport, whether it is passive (facilitated diffusion) or active.
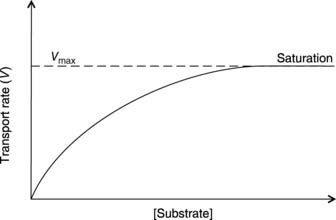
Fig. 4 The rate of transport as a function of substrate concentration for carrier-mediated transport.
Facilitated diffusion
The energy driving facilitated diffusion is the substrate concentration gradient, so this is a passive process, i.e., no additional energy input is required. Movement across the membrane is, nevertheless, dependent on the availability of transport or carrier proteins (Fig. 5). Cellular absorption of glucose from the extracellular fluid is one example.
Active transport
Primary active transport uses the energy released by hydrolysis of ATP, e.g., to transport Na+ out of the cell and K+ into the cell against their electrochemical gradients (the Na+/K+ ATPase, or Na+/K+ pump: Fig. 5).
Secondary active transport uses the energy released during the passive movement of one substance down its electrochemical gradient to transport another substance against a concentration gradient (Fig. 5). For example, sodium cotransport systems couple Na+ diffusion into intestinal cells with the absorption of glucose from the gut lumen (Section 7.4). Absorption can continue even if the concentration of glucose is higher inside the cell than outside. Although the cotransport step itself does not require an external energy source, such systems ultimately depend on active pumping of Na+ back into the extracellular space by Na+/K+ ATPase to maintain the normal Na+ diffusion gradient into the cell.
Vesicular transport
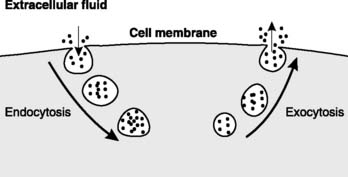
Vesicular transport depends on the transport of substances within membrane-bound vesicles. Limitations on transport resulting from large molecular size and low membrane permeability can be circumvented since the vesicle contents never physically cross the membrane. Endocytosis involves the invagination of a portion of plasma membrane into the cell, which forms a vesicle containing extracellular fluid and near membrane molecules. In exocytosis a vesicle from within the cell fuses with the membrane, releasing its contents to the extracellular fluid (Fig. 6). Exocytosis is particularly important in the release of glandular secretions and chemical transmitters.
1.4 Electrical signals and excitable cells
At the end of this section you should be able to:
Resting membrane potential
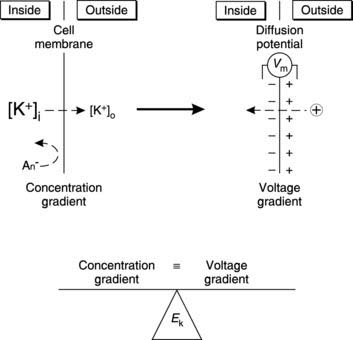
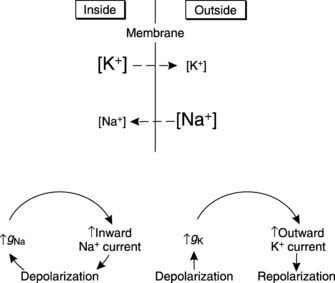
Electrical recordings from nerves show that there is a potential difference of about 70 mV across the cell membrane with the inside negative with respect to the outside. We say that the resting membrane potential is −70 mV. This can be explained by the fact that the cell membrane separates two solutions with different ionic concentrations and is not equally permeable to all the ions involved. As a result, a diffusion potential is generated across the membrane.
Diffusion potentials and equilibrium potentials
Suppose we start with zero electrical potential across the cell membrane (Fig. 7). The concentration of K+ is higher inside the cell than outside and the membrane is permeable to K+, so K+ diffuses outwards. Permeability is selective, however, and the large intracellular anions cannot follow K+. Consequently, an imbalance of charge builds up across the membrane producing a potential difference, with the inside negative with respect to the outside. This is a diffusion potential. The voltage gradient opposes further diffusion of the positive K+ ions, making it more and more difficult for them to leave the cell. The diffusion potential will increase until an equilibrium state is achieved in which the concentration gradient is exactly balanced by the opposing voltage gradient. The potential difference under these conditions is known as the equilibrium potential for K+ (EK). This depends on the ratio of [K+] on either side of the membrane and can be calculated using the Nernst equation:
where R = ideal gas constant, T = absolute (or thermodynamic) temperature (°C + 273K), F = Faraday’s constant and z = ionic valency (+1 for K+).
If we apply this equation to a nerve cell, the concentration of K+ is much higher inside the cell than outside and the calculated value for EK is approximately −90 mV. The measured value of the resting membrane potential (−70 mV) is more positive than this, so it cannot be explained solely in terms of the diffusion potential generated by K+. In fact other ions can also cross the membrane, particularly Na+. The concentration gradient for Na+ is in the opposite direction to K+ (Fig. 9, below) and the calculated value for ENa is approximately +65 mV. The Na+ gradient tends to make the membrane potential more positive than it would otherwise be, but because the resting membrane is much more permeable to K+ than Na+, the resting potential is much closer to EK than ENa. One equation which takes account of the involvement of both K+ and Na+ in determining the resting membrane potential (RMP) is:
Electrogenic ion pumps
Any current flowing across the cell membrane will affect its potential, and one possible source of such currents is the ionic pump which maintains the normal transmembrane concentration gradients. The Na+/K+ ATPase pumps 3Na+ out of the cell for every 2K+ transported in (Fig. 5). This imbalance means that current flows from the inside to the outside of the membrane during active pumping. Such systems are said to be electrogenic and can affect the resting membrane potential. In this case, the net loss of positive charge from inside the cell makes the membrane potential more negative than it would otherwise be. Although this is probably not an important mechanism in determining the resting membrane potential in nerve and striated muscle, it may make a significant contribution in some smooth muscles.
Action potentials
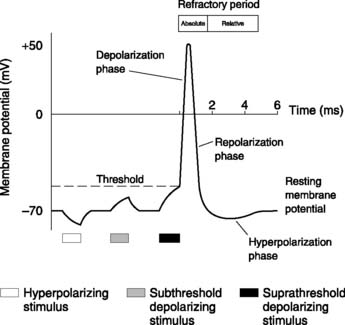
If a nerve cell is stimulated by injecting (positive) electric current, the membrane potential becomes less negative (Fig. 8). We say the membrane potential has reduced (because the magnitude of the potential difference is reduced even though it is less negative) or that the membrane has been depolarized. With small stimuli (subthreshold), the membrane potential simply returns to normal after the stimulus ceases. If, however, the membrane is depolarized to a certain level, known as the threshold potential, the nerve itself generates a series of changes in the potential, known as an action potential. Action potentials are a feature of nerves and muscles, and it is the ability to generate these characteristic electrical signals which typifies excitable tissues.
Action potential properties
Action potentials demonstrate a number of important properties.
Generation of an action potential
The mechanisms responsible for action potential production depend on two main features:
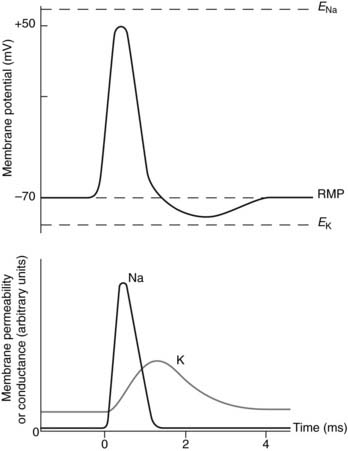
Applying these ideas to nerve action potentials, the resting K+ permeability of the membrane is greater than that to Na+, but any depolarizing stimulus leads to a rapid increase in Na+ permeability. In electrical terms there is an increase in the sodium conductance (gNa). Sodium ions will diffuse into the cell, driven by the high Na+ concentration outside the cell and drawn by the negative charge inside (i.e., by the electrochemical gradient for Na+ which is directed into the cell). The resulting inward sodium current (INa) depolarizes the membrane further setting up a positive feedback loop (Fig. 9). This accounts for the rapid depolarization phase of the action potential. At its peak, the potential comes quite close to ENa because the high Na+ permeability makes it the dominant ion affecting the membrane potential at this time (Fig. 10).
Sodium conductance does not remain high but rapidly falls back to a low level, even though the membrane is depolarized. At the same time the potassium conductance (gK) starts to rise (Fig. 9). This is also a voltage-dependent event induced by membrane depolarization, but it develops more slowly than the changes in gNa. The result is an increase in outward potassium current (IK) driven by the large electrochemical gradient for K+ which exists near the peak of the action potential, when the membrane is very positive relative to EK. This current repolarizes the membrane (Fig. 10). Potassium conductance remains high for some time after the membrane potential has returned to resting levels, causing hyperpolarization as the membrane is driven closer than normal to EK (Fig. 10). Conductance then falls back to normal, and the membrane returns to the resting potential.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree