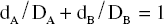WHAT IS SYNERGY?

The term ‘synergy’ is now used very widely, and mainly inaccurately, to describe any kind of positive interaction between drugs. In pharmacology the term has a specific definition, but is often misapplied in practice. Whether an effect can truly be described as synergy, or is merely addition, is rarely established and evidence to prove it conclusively in herbal medicines is sparse. The opposite, antagonism, meaning ‘working against’, is a reduction in the overall expected effect. Put simply, both antagonism and synergism can be defined in relation to an additivity expectation, which can be calculated from the potency of individual mixture components. Synergism is an effect larger than additive, whereas antagonism is smaller than additive. There are two ways of calculating additivity expectations: dose addition and also independent action.

Interactions can also involve a potentiation of effects. The terms ‘synergism’, ‘additivity’ and ‘antagonism’ are applied to combinations where all components induce the effect of interest, whereas the term ‘potentiation’ should be applied where one or several ‘inactive’ compounds enhance or exacerbate the effect of other actives.

Synergy and other interactions can take place between the constituents of a single extract as well as in a mixture of herbs. Medical herbalists have always insisted that better results are obtained with whole plant extracts and combinations of these rather than with isolated compounds. TCM, in particular, uses complicated recipes and it has sometimes been thought that the inclusion of some herbs was unnecessary, but the rationale for such combinations is gaining increasing acceptance. A TCM herbal treatment for eczema was the subject of a clinical trial of 37 young patients (M. P. Sheehan and J. D. Atherton, Br. J. Dermatol., 1992, 126: 179–184), and investigations were carried out to identify the ‘active constituent(s)’ of the mixture. However, a programme of pharmacological tests failed to find a single active herb or compound: it was the herbal mixture that was so effective (J. D. Phillipson, reported in European Phytotelegram, 1994, 6: 33–40).

MEASURING SYNERGY

Although the idea of synergy is easy to understand, the measurement of it is more problematic. It is fairly straightforward to identify synergy when one of the agents is inactive and a combination of this with an active agent produces an effect greater than that observed for the active alone (although this is more correctly termed potentiation), but difficulties in measurement arise when more than one (and there might easily be several) are active. Various methods for calculation have been devised over the years, but the following are now thought to be the most useful:

PREDICTION OF EFFECTS

Synergy is deemed present if the total effect of a combination is greater than would be predicted on the basis of expected additive effects of the mixture. Such additivity expectations can be derived from dose addition or independent action. Often, anticipated additivity is calculated by simply adding up the effects of individual mixture components, but this method can produce paradoxical and erroneous results and is therefore deemed unreliable (A. Kortenkamp and R. Altenburger, 1998; see legend for Fig. 7.1). The opposite applies for antagonism, which is observed less than would have been predicted.

Fig. 7.1 An analysis of combination effects using the isobole method. A, Hypothetical dose–response curves for compounds A and B, and an equimolar mixture of A+B. An effect of 50 is produced by 10 (arbitrary) dose units of A or 100 dose units of B. The combination A+B yields this effect at 5 dose units (2.5 dose units A, 2.5 dose units B). Note that the curves for the individual compounds are dissimilar. B, Diagram showing isoboles for effect level ‘50’ derived from Fig. 7.1A. The solid line (additivity isobole) joining 10 dose units on the A axis and 100 dose units on the B axis describes combinations of A and B that are expected to yield an effect level of ‘50’, if the interaction between A and B is additive. For example, this should be the case with 7.5 dose units A plus 25 dose units B (point 1 on the additivity line), 5 dose units A plus 50 dose units B (point 2) or 2.5 dose units A plus 75 dose units B (point 3). However, the dose–response curves in Fig. 7.1A show that a combination of 2.5 dose units A and 2.5 dose units B is sufficient to produce this effect. Therefore a point below the additivity line is seen, yielding a concave-up isobole. It can be concluded that A and B interact with each other in a way that exacerbates their toxicity (synergism). Conversely, A and B antagonized each other if, e.g., 5 dose units of A plus 75 dose units of B were necessary to produce an effect level of 50 (open square 4). In this case, a point above the additivity line would appear, producing a concave-down isobole. C, Diagram showing isoboles for effect level ‘25’ derived from Fig. 7.1A

(From A. Kortenkamp and R. Altenburger 1998 Synergisms with mixtures of xenoestrogens: a re-evaluation using the methods of isoboles. Science of the Total Environment 221(1): 59–73, with permission.)

THE ISOBOLE METHOD

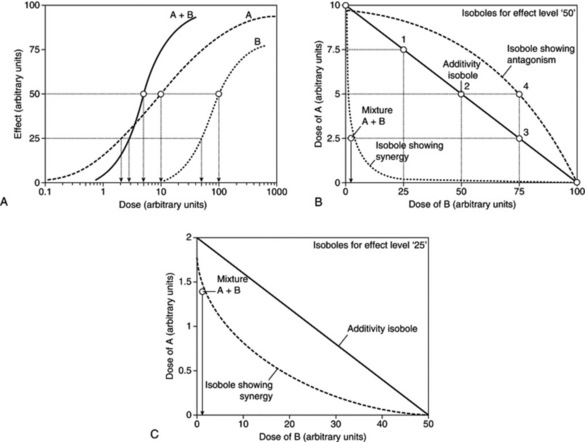
The isobole method is an application of dose addition. It is unequivocal proof of synergy because it is independent of any knowledge of mechanisms and applies under most conditions. It makes no assumptions about the behaviour of each agent and is applicable to multiple components of up to three constituents, so can be applied to the analysis of effects in herbal mixtures. The isobole method uses graphs constructed to show curves (isoboles) describing combinations of two compounds, A and B, which produce the same specified action – which can be any measurable effect (Fig. 7.1A,B). The axes of the graph (Fig. 7.1B) represent doses of the two compounds on a linear scale. A line joining the iso-effective doses A and B of the single agents predicts the combinations of A and B that will yield the same effect, provided the interaction between A and B is only additive. This is the ‘additivity line’, in which case, there is no interaction between the two agents and they could be considered to be behaving like dilutions of each other.

For additivity (zero interaction), the relationship can be expressed algebraically by the equation of Berenbaum (Pharmacol. Rev., 1989 41, 93–141; see Further reading):

However, if synergy occurs, then smaller amounts are needed to produce the effect (i.e. the effect of the combination exceeds expectation) and the equation becomes d_A / D_A + d_B / D_B < 1, and the isobole is said to be ‘concave-up’. The opposite applies for antagonism, and the equation becomes d_A / D_A + d_B/D_B > 1, producing a ‘concave-down’ isobole. It is actually possible to have synergy at a particular dose combination with antagonism at a different combination, and this would be reflected in the isobole. The position of isoboles varies depending on the effect level chosen for analysis (see Fig. 7.1B,C).

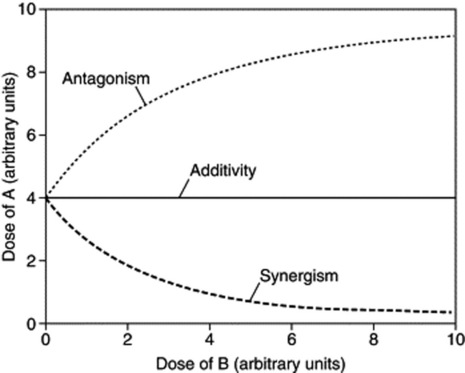
The isobole method can also be applied to mixtures in which only one of the two agents is active; in effect ‘potentiation’. In this case, the iso-effective dose of the agent lacking activity can be regarded as being infinitely large, so the additivity isobole runs parallel to the respective dose axis. Synergism will again yield a concave-up isobole and antagonism a concave-down isobole, as shown in Fig. 7.2.

Fig. 7.2 The three types of combination effect for a mixture of an effective agent A and an ineffective compound B. When there is no interaction between A and B, the isobole is a straight line parallel to the dose axis of B (additivity). If there is a synergistic interaction, an isobole deviating towards the B axis is seen: in the presence of B smaller doses of A are sufficient to produce a predetermined effect. When there is antagonism, the isobole deviates away from the B axis. In this case, the presence of B requires higher doses of A to yield the same effect as in the absence of B.

(From: A. Kortenkamp and R. Altenburger 1998 Synergisms with mixtures of xenoestrogens: a re-evaluation using the methods of isoboles. Science of the Total Environment 221(1): 59–73, with permission.)