Fig. 1
General scheme for Monte Carlo simulation of FRAP on nuclear proteins. Overview of th e COMPARTMENTS that can be defined in the script language. The nucleus is represented as an ellipsoid; the laser double cone is a dedicated compartment that also contains values representing local laser intensities which are stored in a text file that is translated by the program into a 3-D array. (a) Schematic drawing of a cell nucleus (ellipsoid ) containing randomly distributed COMPLEXES (spheres ). Random Brownian motion (inset ) is simulated on the basis of the Einstein–Smoluchowski equation (see text). (b) Simulation of binding to randomly distributed immobile target sites in the DNA (inset ) is simulated by evaluating a chance to bind or to release based on simple binding kinetics, where the ratio between on- and off-rate constants (k on and k off ) equals the ratio between the number of immobile and mobile molecules. (c) Photobleaching is simulated by evaluating a chance to get bleached based on the intensity profile of the laser beam. (Figure adapted from [3])
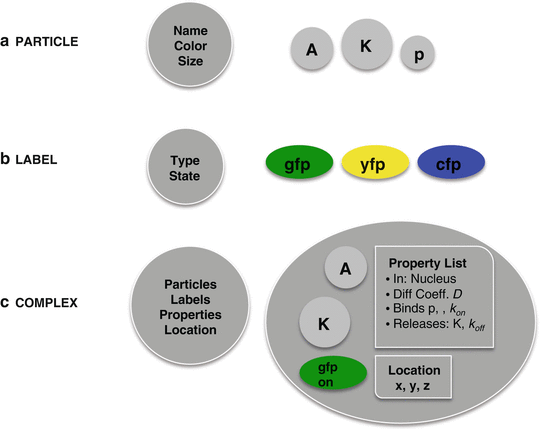
Fig. 2
Overview of the different components in the simulation. (a) PARTICLES are the basic building blocks from which complexes are created. They represent, for instance, proteins, phosphates, or DNA but only acquire properties when added to a complex. (b) LABELS are similar to particles in that they have to be added in a complex. Labels have a reserved name (gfp, yfp, or cfp) and have one property, representing the state of their fluorescent behavior: on, dark, or bleached. (c) COMPLEXES are composed of particles and (optional) labels. When formed, they acquire a property list from a blueprint composed on the basis of the user-defined rules in the script language (see text). They also have x-, y-, and z-coordinates representing their location
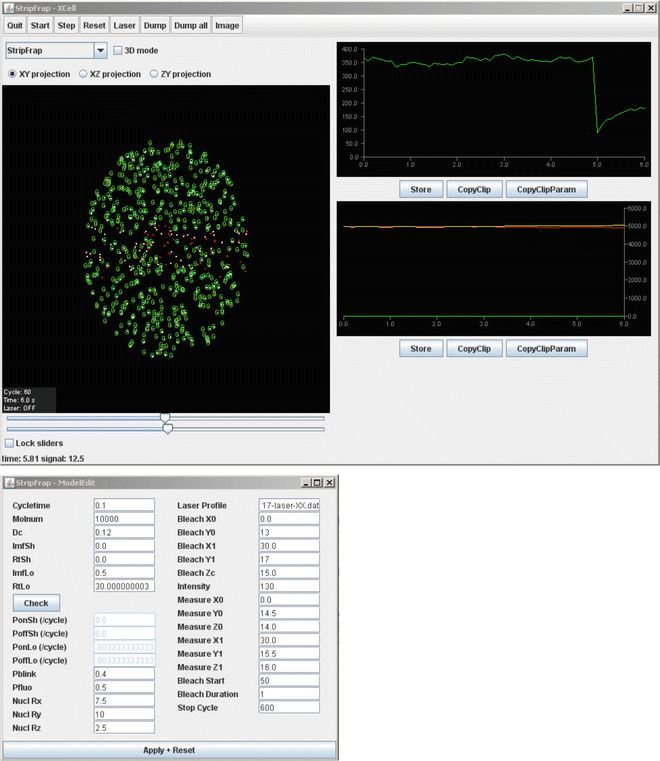
Fig. 3
Graphical interface of the Monte Carlo simulation. The user interface contains two windows; the top window contains the visualization of the COMPLEXES, either fluorescent (red dot with green G) or nonfluorescent (red dot only) and bound (red dot with white dot) or freely mobile (red dot). The two graphs show the number of fluorescent COMPLEXES in the measured strip (FRAP curve) (top) and the sizes of the mobile (red curve), shortly bound (green curve), and long-bound (yellow curve) population in time. The buttons enable export of numerical data in text files. The lower window is used to modify the parameters of the model using indicated variables, including diffusion coefficient (Dc) and binding properties (both short (Sh) and long (Lo) immobile fractions) of the molecules. The binding parameters are set as immobile fractions (Imf) with corresponding residence times (Rt). The software automatically calculates the corresponding probabilities of binding (P on ) or release (P off ). Depending on the fluorophore used in FRAP analysis, the blinking parameters (P blink and P fluo ) should be adjusted. Furthermore, general parameters like nuclear position and size (Nucl), the laser profile for FRAP analysis, and the position and size of the bleached (Bleach) and measured (Measure) areas, in addition to the bleach intensity and duration in cycles, the length of the prebleach period, and the total length of the FRAP curve can be adjusted
The core program is implemented in a straightforward and easily maintainable manner. It translates the user-defined scripts imported through the user interface and sends output to that interface. The program goes through cycles representing small time steps, usually in the order of 10–100 ms. In each cycle, the behavior of each molecule present at that time is simulated by generating random numbers on the basis of which a decision is taken whether the molecule performs specific actions. These decisions are based on probability distributions related to the events happening to the molecule or the actions taken by it. The underlying algorithms dealing with this are described in detail below, where we present the script language, in which compartments, molecules, labels, and their properties are defined. In the user interface, the simulations are visualized, graph and text output relevant for the simulated system is provided, and a number of model-related parameters can be modified by the user (Fig. 3).
3.2.1 Script Language
In order to provide a versatile modelling environment that can be used without the need to write new or modify existing program code, an intuitive script language was developed. The script language consists of a list of definitions of PARTICLES (e.g., proteins, phosphates, DNA), LABELS (gfp, yfp, cfp), COMPLEXES (combinations of particles), and COMPARTMENTS (e.g., nucleus, cytoplasm, laser cone), as well as a series of rules by which specific properties are assigned to the defined complexes. Rules like BIND and RELEASE or ADD and REMOVE define which molecules interact, including corresponding rate constants (k on and k off ), which are translated in the program to probabilities that are evaluated on the basis of numbers generated by a random generator. When the script is translated, the program adds all rules assigned to a specific complex in a property list which serves as a blueprint that is read when the specific complex is actually formed at the start or during the simulation (Fig. 2).
Below, the script language will be explained together with the most important algorithms used in the simulation in the context of the script definition or rule being discussed.
3.2.2 Script Definitions
COMPARTMENT(<NAME>, Compartment type, Fill-file.txt, Parameter list).
Compartments are predefined volumes, which are specified by their reserved-type name followed by a number of parameters that depend on the compartment type. Simple volumes like rectangular boxes (Box) or ellipsoids (Ellipsoid) require the x-, y-, and z-coordinates of their centers and diameters. The laser cone and bleach area (Bleach area) are special volumes that in addition to center and size coordinates, require specification of a formalized text file which contains a table with laser intensities at different positions in the laser.
EXCLUDE( compartment1 , compartment2 );
Compartments like the cytoplasm that contains other compartments like the nucleus are defined by defining two ellipsoids and then exclude the smaller from the larger.
Examples:
COMPARTMENT(nucleus, Ellipsoid, 0,0,0,10,15,5).
COMPARTMENT(cytoplasm, Ellipsoid, 0,0,0,20,20,7).
EXCLUDE(nucleus, cytoplasm).
COMPARTMENT (stripbleach, Bleach area, Laserprofile40X-1.3.txt, 0,0,0,20,1).
PARTICLE (<name>, Colour, Shape, Size).
PARTICLES (Fig. 2a) are the basic building blocks representing units from which COMPLEXES (described below) can be constructed. Particles have a user-defined name, for reference in defining complexes, as well as drawing instructions for visualization in the user interface. The most basic complex contains one particle (see Note 1 ).
Examples:
PARTICLE(transcriptionfactorX, RED, 2).
PARTICLE(kinaseY, RED, 2).
PARTICLE(phosphate, BLUE, 1).
PARTICLE(promotersequence, WHITE, 1).
COMPLEX(particle 1 -particle 2 -…-particle N, Compartment).
COMPLEXES (Fig 2c) consist of user-defined combinations of particles, which are specified by the particle names (see above) separated by hyphens. All possible combinations of particles that exist at the start of the simulation or that may form during the simulation have to be defined. The simplest complex consists of a single particle. The compartment in which the complex is present is the only property defined here. Mobility and interaction properties are assigned by the rules explained in the next section.
Examples
Complexes formed during phosphorylation:
COMPLEX(factorX, nucleus).
COMPLEX(kinaseY, nucleus).
COMPLEX(factorX-kinaseY, nucleus).
COMPLEX(phosphate-factorX-kinaseY, nucleus).
COMPLEX(phosphate-factorX, nucleus).
ADDLABEL(Label, complex).
One or more LABELS (Fig. 2b) can be added to complexes. Currently, three fluorescent labels are supported in the program, gfp, yfp, and cfp. Labels are different from particles in that they have one property of their own (whereas particles have no properties when not in a complex), i.e., they can be in three states: on state, dark state, and bleached. Fluorescent labels are different from particles in that they do not alter the complex property list.
CREATECOMPLEXES (complex, copy number, compartment);
Here, the number of copies of a specific complex present at the start of the simulation is specified. Note that only after this definition, actual complexes are formed. When complexes are created, their property list is read from a blueprint that was composed from the rules specified for each complex type while the script was read.
Example:
CREATECOMPLEXES (A, 10,000, nucleus).
3.2.3 Script Rules
Rules assign properties to COMPLEXES. When the script is read, the blueprint property list of each defined complexes is (which after complex definition contains one property, the compartment it is in) built up from properties derived from the rules (see also Fig. 3).
MOVE(complex, Diffusion Coefficient, Compartment).
The MOVE rule adds a diffusion coefficient to the complex blueprint property list. In the simulation, diffusion is simulated on the basis of the Einstein–Smoluchowski equation which defines the mean square displacement MSD of a pool of particles as MSD = 2nDt, where D is the diffusion coefficient, t is time, and n is the number of dimensions in which the particles diffuse. In the simulation core program, 3-D diffusion of individual complexes is simulated by moving each complex in x-, y-, and z-direction, over a distance obtained by generating a random number R from a uniform distribution, and subsequently computing G(R) where G is a cumulative inverse Gaussian distribution with μ = 0 and σ2 = 2Dt (see Note 2 ).
Anomalous diffusion can be simulated by using the ADD and REMOVE rule described below, adding and removing a (virtual) particle, with high on- and off-rate constants. The definitions and rules needed are described in an example below, where the ADD and REMOVE rules are described.
BIND(complex 1 , complex 2, Compartment, rate constant, ).
RELEASE(complex 1 , complex1-complex 2 , rate constant, Compartment).
The BIND rule assigns the property that complexes may bind to each other when they collide, and in which compartment this property is valid. A rate constant, k on , is specified in s−1. The chance of binding upon collision between complexes is derived by the program dependent on the duration of the simulated time step. In a relatively simple binding algorithm, the user-specified rate constant and the distance between two molecules under consideration together determine the chance that the two actually bind. We applied two different strategies for calculating the binding chance. In the first simple approach, the binding chance derived from k on is applied when the distance between two molecules is smaller than a user-defined threshold. In a second more complex approach, the chance of collision is retrieved from a 3-D look-up table that gives the chance that two molecules with diffusion coefficients D1 and D2 collide when they are at distance d. The chance in each table cell (D1, D2, d) was estimated by performing a large number of MC simulations at very small time steps of 0.1 ms, for each table cell, and counting the times the two molecules collide, i.e., come closer than 1 nm.
The RELEASE rule assigns the property to a complex that part of the complex may detach and in which compartment this property is valid. The rate constant, k off , is specified here in s−1 and translated by the program to the actual chance per simulated time step.
Examples:
BIND (A, B, nucleus, 0.01).
RELEASE (A, A-B, nucleus, 0.01).
ADD (complex 1 , complex 2 , rate constant, compartment).
REMOVE (complex 1 , complex 2 , rate constant, compartment).
ADD and REMOVE are similar to BIND and RELEASE, with the very important difference that added or removed complexes do not exist independently in the simulation, but are created by ADD, and taken up in the complex, or destroyed by REMOVE. The rate constant is therefore in both cases in s−1, that is, independent of concentration. ADD and REMOVE rules can and should be used only when variations in spatial distribution and concentration of the added or removed complex are negligible during the simulation, i.e., when its concentration is in excess compared to the complex it is added to or removed from, and no local depletion or accumulation occurs. This is, for instance, useful for abundant phosphates or other small compounds.
Examples
Addition of a phosphate by a kinase and removal by a phosphatase:
ADD (phosphate, txnfactorX-KinaseY, nucleus, 0.5).
REMOVE (phosphate, txnfactorX-phosphate-PhosphataseY, nucleus, 0.5).
Simulation of anomalous diffusion:
ADD (anomdiffparticle, A, nucleus, 0.9).
REMOVE (anomdiffparticle, A-anomdiffparticle, nucleus, 0.9).
MOVE (A, 5, nucleus).
MOVE (A-anomdiffparticle, 0.01, nucleus).
BLEACH (start time, stop time, label, bleach area).
If a molecule contains a fluorescent label, this label can be bleached by a laser. We have implemented two approaches to define the laser intensity profile of the laser. In a simple approach, a theoretical intensity distribution was used based on a Gaussian distribution of intensities. In a second approach, the laser profile was experimentally determined by photobleaching a homogeneous fluorescent test slide with a focused stationary laser beam and measuring the bleach intensities at different optical sections spaced 1 μm. These values were then translated to laser intensities. Bleaching will take place during the simulation between the specified start and stop times in the bleach area defined in the definition section. For example:
COMPARTMENT (spotbleach, Bleach area, Laserfile.txt, 0,0,0).
BLEACH (100,101, gfp, spotbleach).
bleaches a spot at (0, 0, 0), usually the center of an ellipsoid representing the nucleus, during two simulated time steps.
3.3 Simulation of FRAP and FRET Assays
The simulation software was originally developed to quantitatively analyze FRAP applied to proteins in the cell nucleus. In addition, it provides a useful tool to study the influence of experimental conditions like the shape and size of the volume in which the proteins under surveillance reside as well as of the shape, size, and position of the bleach area. These two applications will be studied in the next two sections. In a third section, we will demonstrate the combination of acceptor photobleaching FRET and FRAP, which generates highly complex data.
3.3.1 FRAP Simulation, Fitting Experimental Data
There are basically three ways to fit simulation-generated FRAP curves to a given experimental curve:
1.
Trial-and-error interactive search (Fig. 4). This approach requires some experience with the specific FRAP method. For instance, in a strip-FRAP experiment applied to the cell nucleus, which we routinely apply, one can start comparing an inactive situation, for instance, a non-DNA-binding mutant androgen receptor (AR) with an active situation, the activated wild-type AR. Then assume that the inactive molecules are freely mobile and try to fit with models of free diffusion (Fig. 4b). Then, when fitting the active situation, fix the best fitting diffusion coefficient and introduce an immobile fraction. This fraction can initially be estimated roughly, by checking how far recovery has proceeded at the time the freely mobile protein is fully recovered. The residence time can initially be estimated by checking time until full recovery (Fig. 4a).
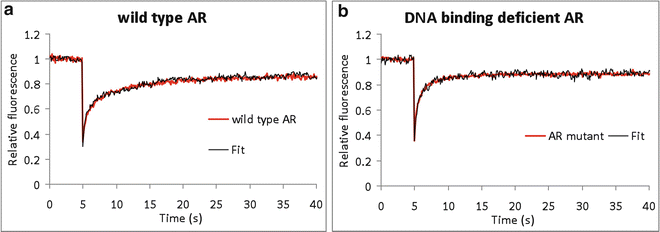

Fig. 4
Applications of FRAP in biological model systems. Two examples of the use of FRAP simulation of nuclear proteins (a, b), the androgen receptor (AR) (a) with its DNA-binding deficient mutant (b). (a) Like most nuclear proteins, the transcription factor AR shows a high mobility and in addition to transient immobilizations. The wild-type AR curve was best fitted to a curve representing a Dc of 1.9 μm2/s and fraction of 35 % of the ARs immobilized for 8 s. This immobilization is due to DNA binding as is shown by a FRAP analysis of (b), a DNA-binding deficient AR, which fitted best to a scenario of freely mobile molecules (Dc = 1.9 μm2/s). Experimental curves are red; simulated curves are black. The fit was performed by interactive trial-and-error modelling
2.




Creating a large database in which all parameters to be fitted are systematically varied. We have extensively applied this approach in many studies investigating a variety of nuclear model systems [24–34]. Briefly, the experimenter first provides a number of fixed parameters, including the experimentally derived size of the nuclei, the FRAP approach, and the lens used for photobleaching and recording. Then a database is created where diffusion and DNA-binding properties (on- and off-rate constants) are systematically varied. Note that usually the rate constants are translated to intuitively better understandable immobile fraction and residence time (cf. Fig. 1b). In some cases, we also fitted a second pair of on- and off-rate constants representing short immobilization events [31, 33, 35]. When the database is created, a set of 20–50 simulated curves that fit best to the experimental curve are generated. In practice, there will be two or sometimes more different scenarios represented of which usually only one is realistic in the view of the system under surveillance. From the 5–10 best fitting curves, the diffusion and binding parameters are then averaged and considered best estimates.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


