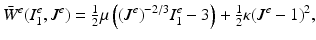is a one-to-one (bijective) mapping [4, 12, 19]
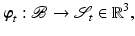
(1)
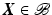from the reference configuration 
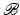onto positions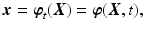
(2)
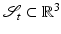at time t ∈ [0, T]. A fundamental measure of deformation is the deformation gradient [19]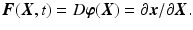
(3)
![$$\displaystyle{ J(\boldsymbol{X}) =\det [F(\boldsymbol{X})]> 0. }$$
” src=”/wp-content/uploads/2016/10/A321864_1_En_4_Chapter_Equ4.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(4)</DIV></DIV><br />
<DIV></DIV><br />
<DIV class=Para>Deformation due to swelling or shrinking can be introduced by considering a (fictitious) stress-free intermediate configuration <SPAN id=IEq8 class=InlineEquation><IMG alt=](/wp-content/uploads/2016/10/A321864_1_En_4_Chapter_IEq8.gif)
between the initial configuration 
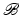and the deformed configuration 
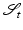(Fig. 1). This concept was first developed by Flory and Rehner [7] for swelling of polymers [5] and is similar to that used for metal plasticity [19], thermal expansion [11] and biological growth [18]. The total deformation 
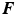can be separated into elastic 
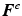and swelling deformation 
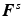by a local multiplicative decomposition of the form [2, 11, 18]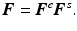
(5)
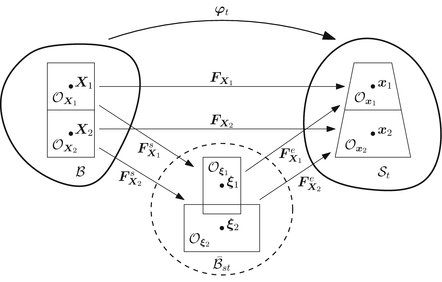
Fig. 1
Multiplicative decomposition of the deformation gradient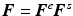 
for the motion of two adjacent material points 
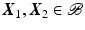to the spatial positions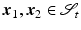 
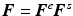for the motion of two adjacent material points 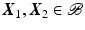to the spatial positions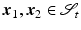 It should be understood that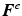 
and 
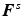are not proper gradients and that the intermediate configuration is incompatible in a global sense as indicated by the overlapping neighbourhoods 
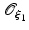and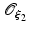 
of the points 
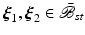(Fig. 1) [13, 19]. Conceptually, the multiplicative decomposition can be thought of as the disassembly of a finite element mesh (the initial undeformed configuration) and the subsequent application of the local volumetric deformation due to swelling on the individual elements. Unless the swelling deformation is homogeneous, this intermediate configuration will be incompatible at the boundaries between elements and the elements will no longer “fit together” (more precisely, the intermediate configuration is not a proper configuration because—except for the special case of homogeneous swelling—a bijective mapping between the material particles and 
does not exist [6]). Compatibility of the final (deformed) configuration is enforced by reassembling the mesh using the nodal connectivity of the elements. For a formal exposition of the geometrical details, the reader is referred to [6, 12, 13].
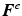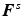and are not proper gradients and that the intermediate configuration is incompatible in a global sense as indicated by the overlapping neighbourhoods 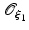and 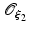of the points 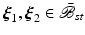(Fig. 1) [13, 19]. Conceptually, the multiplicative decomposition can be thought of as the disassembly of a finite element mesh (the initial undeformed configuration) and the subsequent application of the local volumetric deformation due to swelling on the individual elements. Unless the swelling deformation is homogeneous, this intermediate configuration will be incompatible at the boundaries between elements and the elements will no longer “fit together” (more precisely, the intermediate configuration is not a proper configuration because—except for the special case of homogeneous swelling—a bijective mapping between the material particles and 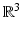does not exist [6]). Compatibility of the final (deformed) configuration is enforced by reassembling the mesh using the nodal connectivity of the elements. For a formal exposition of the geometrical details, the reader is referred to [6, 12, 13].For isotropic swelling the swelling deformation gradient can be written as
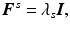
where λ s is the isotropic swelling stretch and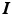 
is the identity tensor. The elastic deformation gradient can then be expressed simply as
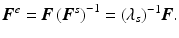
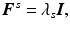
(6)
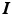is the identity tensor. The elastic deformation gradient can then be expressed simply as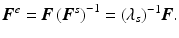(7)
The total Lagrangian (TL) formulation of the finite element method uses rotation invariant measures of strain (Green–Lagrange strain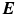 
) and stress (second Piola–Kirchhoff stress 
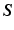) that are calculated with respect to the initial (undeformed) reference configuration 
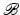[3, 4]. The deformations 
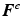and 
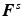satisfy the invertibility and impenetrability of matter requirements so that the usual push-forward and pull-back operations can be performed to obtain the stress measures with respect to the configurations 
, 
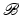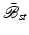and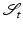 
[13]. For convenience, the (effective) elastic second Piola–Kirchhoff stress 
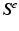is introduced by the push-forward of 
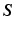onto the relaxed intermediate configuration 
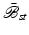scaled by the volume ratio J s . The (total) second Piola–Kirchhoff stress with respect to the initial reference configuration 
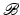can then be expressed as
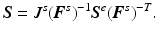
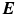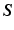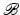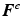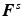) and stress (second Piola–Kirchhoff stress ) that are calculated with respect to the initial (undeformed) reference configuration [3, 4]. The deformations and satisfy the invertibility and impenetrability of matter requirements so that the usual push-forward and pull-back operations can be performed to obtain the stress measures with respect to the configurations 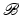, 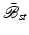and 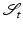[13]. For convenience, the (effective) elastic second Piola–Kirchhoff stress 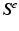is introduced by the push-forward of 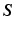onto the relaxed intermediate configuration 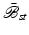scaled by the volume ratio J s . The (total) second Piola–Kirchhoff stress with respect to the initial reference configuration 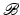can then be expressed as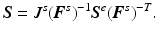(8)
In practice, when using hyperelastic materials with the TL formulation of the FE method,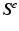 
is computed using invariants of the elastic deformation gradient 
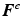, whereas the nodal forces are usually computed using 
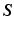and the total deformation gradient 
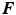with respect to the initial reference configuration [3, 4]. This enables the swelling behaviour to be included entirely within the material constitutive model. Standard element formulations can then be used to calculate the element nodal forces and displacements in the usual manner. The Cauchy stress can be obtained using the inverse Piola transformation
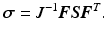
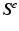is computed using invariants of the elastic deformation gradient 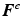, whereas the nodal forces are usually computed using 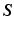and the total deformation gradient 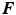with respect to the initial reference configuration [3, 4]. This enables the swelling behaviour to be included entirely within the material constitutive model. Standard element formulations can then be used to calculate the element nodal forces and displacements in the usual manner. The Cauchy stress can be obtained using the inverse Piola transformation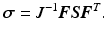(9)
2.2 Constitutive Material Model
At low strain rates the mechanical behaviour of soft tissues can be characterised using a hyperelastic constitutive law [22]. Viscoelastic effects are ignored due to the relatively slow loading speed involved with soft tissue swelling (on the order of a few hours).
Hyperelastic materials are characterised by the existence of a strain energy function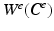 
that relates the deformation to the second Piola–Kirchhoff stress
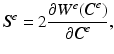
where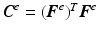 
is the elastic right Cauchy–Green deformation tensor [4]. For hyperelastic materials that are isotropic with respect to the initial, unstressed configuration the strain energy density 
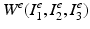can be expressed in terms of the principal invariants 
, 
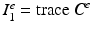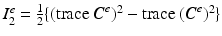and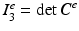 
[4]. The classical (incompressible) neo-Hookean model with strain energy density 
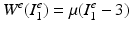is based on the assumption that the deformation is isochoric (J e = 1). To account for (slight) compressibility of the material we use the modified strain energy density [24]
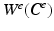that relates the deformation to the second Piola–Kirchhoff stress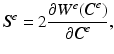(10)
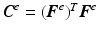is the elastic right Cauchy–Green deformation tensor [4]. For hyperelastic materials that are isotropic with respect to the initial, unstressed configuration the strain energy density 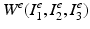can be expressed in terms of the principal invariants 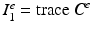, 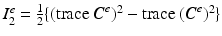and 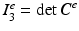[4]. The classical (incompressible) neo-Hookean model with strain energy density 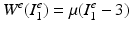is based on the assumption that the deformation is isochoric (J e = 1). To account for (slight) compressibility of the material we use the modified strain energy density [24]
