12
Accuracy of measurement
Consider the following statement:
The dispensary is 15.342 metres long
In the 15.342 metres, the last figure, 2, is in the millimetres column and so the length of the dispensary in millimetres is 15 342. It is unlikely that anyone would want to know the length of the room to that degree of accuracy and it is also unlikely that the measurements could be made to that degree of accuracy without very specialised equipment. The figure 2 is likely to be unnecessary and may also be misleading, implying that the measurement is more accurate than it really is.
Sometimes we need to express numbers ‘to the nearest’. For example, if we need the above dispensary length to the nearest centimetre, the result would be 1534 cm. Its length to the nearest metre would be 15 metres. This ‘to the nearest’ approach brings us to the technique of rounding.
Rounding numbers
Rounding is used to make numbers more convenient or smaller so that numbers are easier to work with, especially if you are trying to work the answers out in your head. However, rounded numbers are only approximate and so an exact answer, generally, cannot be obtained using rounded numbers.
In order to round a number we look, normally, at the last figure or figures:
If the number ends in 1 to 4, then the number is converted to the next lower number that ends in 0. For example, 54 rounded to the nearest 10 becomes 50.
If the number ends in 5 to 9, then the number is converted to the next higher number ending in 0. For example, 58 rounded to the nearest 10 becomes 60.
Rounded numbers are used to get an answer that is close to the exact answer, but is unlikely to be the exact number. For example, if we need to add together 199 and 2254, then by rounding each number to the nearest 10:
199 becomes 200 and
2254 becomes 2250
The total of the two rounded numbers is 2450 compared with the total of the unrounded numbers, which is 2453.
The technique of rounded numbers is used to reduce a number with several figures to one with fewer figures or to reduce a number with a large number of figures after the decimal place to a more convenient or manageable size.
Significant figures
Converting the dispensary length from nearest metres (15) to nearest centimetres gives a length of 1500 centimetres. In this number, the 1 means one thousand, the 5 means five hundreds, but the 00 does not mean 0 tens and 0 units. The 00 means that the number of tens and the number of units are not stated. The zeros are there to act as spacers so that the 1 appears in the thousands column and the 5 appears in the hundreds column. As the 1 and the 5 mean what they say, they are significant figures. The two zeros are not significant figures.
Note: if a number is stated in the form 0.340 (rather than 0.34) and we are not told to what degree of accuracy the number is stated, the zero to the right of the 4 would be interpreted as indicating that there are no thousandths and that the number was correct to the nearest thousandth. There would be three significant figures. This way of expressing numbers is used to convey the degree of precision required in weights and measurements (see later).
Correcting to fewer significant figures
In order to correct 33.62 to two significant figures, we consider the first three significant figures. Using the rounding technique, 33.62 corrected to two significant figures is 34.
Similarly, in order to correct 33.42 to two significant figures, we consider the first three significant figures. Using the rounding technique, 33.42 corrected to two significant figures is 33.
Correcting to a certain number of decimal places
The method used is similar to that described above to deal with correction to a certain number of significant figures and again involves the rounding technique.
Look at the figure in the column to the right of the last decimal place required. If the figure is 4 or less, it and any digits to the right of it are deleted. If the digit is a 5 or higher, the digit of the last decimal place is increased by 1 and any digits to the right are deleted.
Accuracy in arithmetic calculations
If all the values involved in a calculation are exact then it will be possible to calculate the exact value of the result. If, however, some of the values involved in a calculation are inexact and have been stated to a certain number of significant figures, a decision needs to be made as to how many figures of the result are likely to be significant.
If the arithmetic operations involve addition and/or subtraction, then the rule applied states that the result should be rounded to the precision of the least precise approximate number involved. For example, assume in the following calculation that all numbers have been rounded and so are approximate.
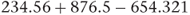
The apparent result is 456.739. This result is to three decimal places. However, if we look at the three original numbers, the least precise is 876.5 because it is expressed only to one decimal place. If we apply the rule, then the result should be expressed and rounded to one decimal place, i.e. 456.7.
If the arithmetic operations involve multiplication and/or division, the rule is to find the number in the calculation that has the least number of significant figures, and to round the result to that number of significant figures. For example, assume in the following calculation that all the numbers have been rounded and so are approximate.
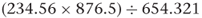
The apparent result using a calculator is 314.206 3911. If we look at the three original numbers, the one with the least number of significant figures is 876.5 with four significant figures. If we apply the rule the result should be expressed and rounded to four significant figures, 314.2.
However, be aware that the actual number of reliable significant figures could be even smaller. Throughout a calculation, numbers should be retained to more significant figures than those required in the final result and correcting to the required number of significant figures should be carried only out at the end of the calculation.
Errors built up in arithmetic calculations
When, because of measuring difficulties, numbers are stated as estimates to a certain number of significant figures, errors are introduced. Further errors are built up when calculations are carried out and, if there is a need to keep a close check on the extent of the errors, it is possible to do so by finding lower and upper bounds for the possible values of the result.
As an example of this approach, consider the expression:
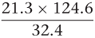
where each number is rounded and stated correct to one decimal place.
| 21.349 corrected to three significant figures becomes 21.3 |
| 21.312 corrected to three significant figures becomes 21.3 |
| 21.273 corrected to three significant figures becomes 21.3 |
| 21.251 corrected to three significant figures becomes 21.3 |
Thus, we can see that any number in the interval from 21.25 to 21.35 (but not including the number 21.35) will be represented by the number 21.3 after correction to three significant figures. So in using 21.3 there is a possible error of up to 0.09. Similarly, 124.6 represents any number in the interval from 124.55 to 124.65 and 32.4 represents any number in the interval from 32.35 to 32.45.
When 21.3 is multiplied by 124.6, the smallest value that can be obtained is the one achieved by multiplying the smallest value represented by 21.3 by the smallest value represented by 124.6, i.e. 21.25 × 124.55, giving 2646.6875. The smallest value of the result will be obtained by dividing 2646.6875 by the largest value represented by 32.4, i.e. 32.45, giving 81.562 018.
When 21.3 is multiplied by 124.6, the largest value that can be obtained is the one achieved by multiplying the largest value represented by 21.3 by the largest value represented by 124.6, i.e. 21.35 × 124.65, giving 2661.2775. The largest value of the result will be obtained by dividing 2661.2775 by the smallest value represented by 32.4, i.e. 32.35, giving 82.265 147.
We have found lower and upper limits of 81.562 018 and 82.265 147 for the result of the calculation. Using a calculator to evaluate the expression, the result is 81.912 963. Each of these three values becomes 82 when corrected to two significant figures. Applying the rule stated above, values 21.3 and 32.4 are those involved in the calculation that have the least number of significant figures. Correcting the calculator result to the same number of significant figures gives 81.9, but we see that there is a possible error of about 0.35, so the third figure is in doubt. This supports the warning expressed earlier that the actual number of reliable significant figures may be smaller than that provided by the rule.
Accuracy in weighing/measuring for pharmaceutical tests and assays
The European Pharmacopoeia (EP) gives instructions for dealing with accuracy and precision. In tests and assays, the stated quantity to be taken is approximate, but the amount actually used is accurately weighed and the result is calculated from this exact quantity. In addition, the amount actually weighed may deviate by not more than 10% from that stated. The EP also gives instructions for quantities weighed or measured, which must have an accuracy commensurate with the indicated degree of precision. For example, in the case of weighing, the precision corresponds to plus or minus 5 units after the last figure stated, thus 0.25 g is to be interpreted as 0.245 g to 0.255 g. This is an example of rounding. The degree of precision is implied by the number of significant figures.
Use the following information to complete Examples 12.12, 12.13 and 12.14.
The EP states that erythromycin ethyl succinate should contain not more than 3.0% water determined on 0.300 g by semi-micro determination of water and not more than 0.3% of sulfated ash determined on 1.0 g.



