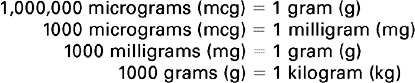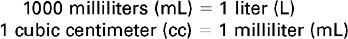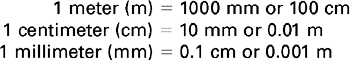Metric and Household Measurements
LEARNING OBJECTIVES
On completion of the materials provided in this chapter, you will be able to perform computations accurately by mastering the following mathematical concepts:
1 Recalling the metric measures of weight, volume, and length
2 Computing equivalents within the metric system by using a proportion
3 Recalling approximate equivalents between metric and household measures
4 Computing equivalents between the metric and household systems of measure by using a proportion
METRIC MEASUREMENTS
The metric system has become the system of choice for dealing with the weights and measures involved in the calculation of drug dosages. This is a result of its accuracy and simplicity because it is based on the decimal system. The use of decimals tends to eliminate errors made when working with fractions. Therefore all answers within the metric system need to be expressed as decimals, not as fractions.
Certain prefixes identify the multiples of 10 that are being used. The four most commonly used prefixes of the metric system involved with the calculation of drug dosages are the following:
These prefixes may be used with any of the base units of weight (gram), volume (liter), or length (meter). The nurse most often uses the following list of metric measures (Box 6-1). Memorize all the entries in the list.
BOX 6-1
Metric Measure of Weight
Metric Measure of Volume
Metric Measure of Length
Sometimes, to compute drug dosages, the nurse must convert a metric measure to an equivalent measure within the system. This may be done easily by using a proportion.
EXAMPLE: 300 mg equals how many grams?
a. On the left side of the proportion, place what you know to be an equivalent between milligrams and grams. From the preceding chart we know that there are 1000 mg in 1 g. Therefore the left side of the proportion would be
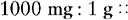
b. The right side of the proportion is determined by the problem and by the abbreviations used on the left side of the proportion. Only two different abbreviations may be used in a single proportion. The abbreviations must also be in the same position on the right as they are on the left.
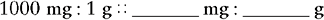
From the problem we know we have 300 mg.
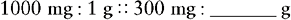
We need to find the number of grams 300 mg equals, so we use the symbol x to represent the unknown. Therefore the full proportion would be
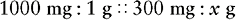
c. Rewrite the proportion without using the abbreviations.
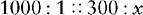
d. Solve for x by multiplying the means and extremes. Write the answer as a decimal, since the metric system is based on decimals.
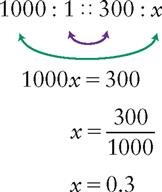
e. Label your answer, as determined by the abbreviation placed next to x in the original proportion.
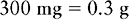
EXAMPLE 1: 2.5 L equals how many milliliters?
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
