METHODS OF CALCULATION
Objectives
Before drug dosage can be calculated, units of measurement must be converted to one system. If the drug is ordered in grams and comes in milligrams, then grams are converted to milligrams or milligrams are converted to grams.
Four methods for calculating drug dosages include basic formula, ratio and proportion, fractional equation, and dimensional analysis. The ratio and proportion and fractional equation methods are similar. For drugs that require individualized dosing, body weight and body surface area are used. When body weight and body surface area calculations are used, one of the first four methods for calculation is necessary to determine the amount of drug needed from the container.
At some institutions, the nurse orders enough medication doses for a designated period. If the order requires 2 tablets, qid (4 times a day) for 5 days, then the number of tablets needed would be 2 tablets × 4 times a day × 5 days = 40 tablets.
DRUG CALCULATION
The four methods as mentioned for drug calculations are (1) basic formula, (2) ratio and proportion, (3) fractional equation, and (4) dimensional analysis (factor labeling).
Method 1: Basic Formula
The following formula is often used to calculate drug dosages. The basic formula (BF) is the most commonly used method, and it is easy to remember.
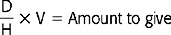
D or desired dose: drug dose ordered by physician or health care providers (HCPs).
H or on-hand dose: drug dose on label of container (bottle, vial, ampule)
V or vehicle: form and amount in which the drug comes (tablet, capsule, liquid)
EXAMPLES
PROBLEM 1: Order: erythromycin (ERY-TAB) 0.5 g, po, q8h.
Drug available:

a. Both the dosage of the drug ordered and the dosage on the bottle are in the metric system; however, the units of measurement are different. Conversion is needed. To convert grams to milligrams, move the decimal point three spaces to the right (see Chapter 1: Systems Used for Drug Administration):
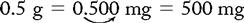
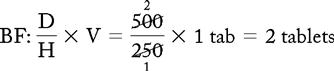
Answer: erythromycin 0.5 g = 2 tablets
PROBLEM 2: Order: 0.5 g of ampicillin (Principen), po, bid.
Drug available:

a. The unit of measurement that is ordered and the unit on the bottle are in the same system but in different units; therefore, conversion of units within the same system must be done first. To convert grams to milligrams, move the decimal point three spaces to the right (see Chapter 1, Systems Used for Drug Administration):
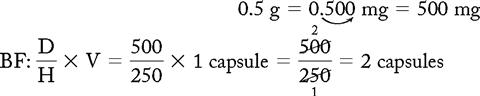
Answer: ampicillin (Principen) 0.5 g = 2 capsules
PROBLEM 3: Order: phenobarbital 120 mg, STAT.
Drug available: phenobarbital 30 mg per tablet.
a. Conversion of unit of measurement is NOT needed for both are of the same unit, milligrams.
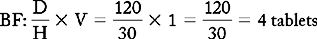
Answer: phenobarbital 120 mg = 4 tablets
PROBLEM 4: Order: meperidine (Demerol) 35 mg, IM, STAT.
Drug available:

a. Conversion is not needed, because both are of the same unit of measurement.
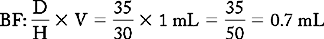
Answer: meperidine (Demerol) 35 mg = 0.7 mL
Method 2: Ratio and Proportion
Ratio and proportion (RP) is the oldest method used for calculating dosage problems:

EXAMPLES
PROBLEM 1: Order: erythromycin (ERY-TAB) 0.5 g, po, q8h.
Drug available:

a. To convert grams to milligrams, move the decimal point three spaces to the right (see Chapter 1 “Systems Used for Drug Administration”):
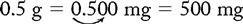
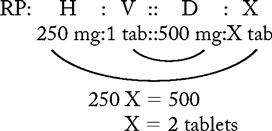
Answer: erythromycin 0.5 g = 2 tablets
Note: With RP, the ratio on the left (milligrams to tablets) has the same relation as the ratio on the right (milligrams to tablets); the only difference is values.
PROBLEM 2: Order: aspirin (ASA) 650 mg, PRN.
Drug available: aspirin 325 mg per tablet.

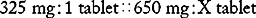
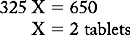
Answer: aspirin 650 mg = 2 tablets
PROBLEM 3: Order: amoxicillin 75 mg, po, qid.
Drug available:
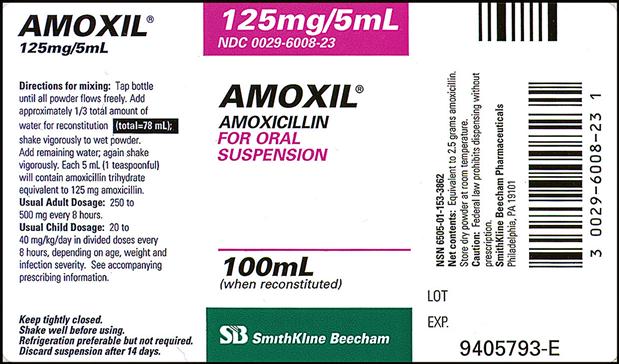
125 X = 375
X = 3 mL
Answer: amoxicillin 75 mg = 3 mL
PROBLEM 4: Order: meperidine (Demerol) 60 mg, IM, STAT.
Drug available:

a. Conversion is not needed; the same unit of measurement is used.
100 mg:1 mL::60 mg:X mL
100 X = 60
X = 0.6 mL
Answer: meperidine (Demerol) 60 mg = 0.6 mL
Method 3: Fractional Equation
The fractional equation (FE) method is similar to RP, except it is written as a fraction.
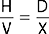
H: the dosage on hand or in the container
V: the vehicle or the form in which the drug comes (tablet, capsule, liquid)
Cross multiply and solve for X.
EXAMPLES
PROBLEM 1: Order: kanamycin sulfate (Kantrex) 1 g, po, q6h × 3 days.
Drug available:

a. Convert grams to milligrams. Move the decimal point three spaces to the right.
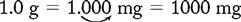
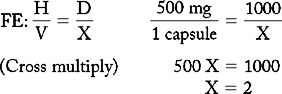
Answer: kanamycin 1 g = 2 capsules
PROBLEM 2: Order: valproic acid (Depakene) 100 mg, po, tid.
Drug available: valproic acid (Depakene) 250 mg/5 mL suspension.
a. No unit conversion is needed.
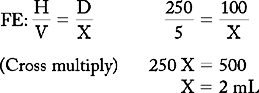
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


