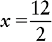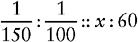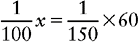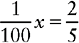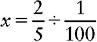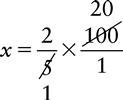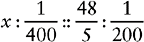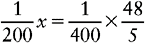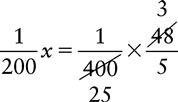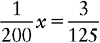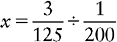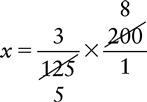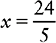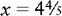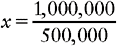Proportions
Proportions
LEARNING OBJECTIVES
On completion of the materials provided in this chapter, you will be able to perform computations accurately by mastering the following mathematical concepts:
1 Solving simple proportion problems
2 Solving proportion problems involving fractions, decimals, and percents
Most problems concerning drug dosage can be solved by a proportion problem, whether it involves fractions, decimals, or percents. If a proportion problem contains any combination of fractions, decimals, or percents, all forms within the problem must be converted to either fractions or decimals.
Study the introductory material on proportions. The process for the calculation of proportion problems is listed in steps. Memorize the steps before beginning the work sheet. Complete the work sheet at the end of this chapter, which provides for extensive practice in the manipulation of proportions. Check your answers. If you have difficulties, go back and review the necessary steps. When you feel ready to evaluate your learning, take the first posttest. Check your answers. An acceptable score as indicated on the posttest signifies that you are ready for the next chapter. An unacceptable score signifies a need for further study before taking the second posttest.
![]() A proportion consists of two ratios of equal value. The ratios are connected by a double colon (::), which symbolizes the word as.
A proportion consists of two ratios of equal value. The ratios are connected by a double colon (::), which symbolizes the word as.
2 : 3 :: 4 : 6
Read the above proportion: “Two is to three as four is to six.”
The first and fourth terms of the proportion are the extremes. The second and third terms are the means.
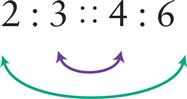
2 and 6 are the extremes
3 and 4 are the means
A helpful way to remember the correct location of the extremes and means is
E = The end of the problem
M = The middle of the problem
In a proportion the product of the means equals the product of the extremes because the ratios are of equal value. This principle may be used to verify your answer in a proportion problem.
3× 4 = 12, product of the means
2 × 6 = 12, product of the extremes
If three terms in the proportions are known and one term is unknown, an x is inserted in the space for the unknown term.
2 : 3 :: 4 : x
SOLVING A SIMPLE PROPORTION PROBLEM
4. Divide the product of the known terms by the number next to x. The quotient will be the value of x.
Proportion Problem Involving Whole Numbers
Proportion Problem Involving Fractions
Proportion Problem Involving Decimals
EXAMPLE: 0.4 : 0.8 :: 0.25 : x
Proportion Problem Involving Fractions and Percents
EXAMPLE:
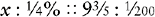
Convert ¼% to a proper fraction and 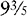 to an improper fraction. Then rewrite the proportion using these fractions.
to an improper fraction. Then rewrite the proportion using these fractions.
Proportion Problem Involving Decimals and Percents
EXAMPLE: 0.3% : 1.8 :: x : 14.4
Proportion Problem Involving Numerous Zeros
EXAMPLE: 250,000 : x :: 500,000 : 4