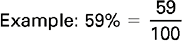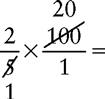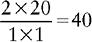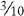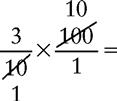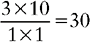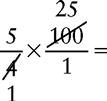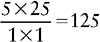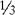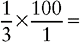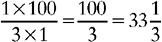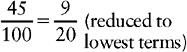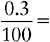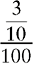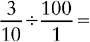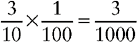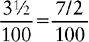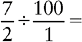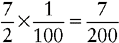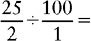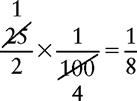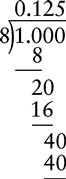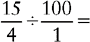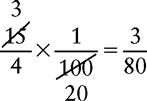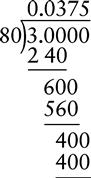Percents
LEARNING OBJECTIVES
On completion of the materials provided in this chapter, you will be able to perform computations accurately by mastering the following mathematical concepts:
1 Changing a fraction or decimal to a percent
2 Changing a percent to a fraction or decimal
3 Changing a percent containing a fraction to a decimal
4 Finding what percent one number is of another
Study the introductory material on percents. The processes for the calculation of percent problems are listed in steps. Memorize the steps for each calculation before beginning the work sheet. Complete the work sheet at the end of this chapter, which provides for extensive practice in the manipulation of percents. Check your answers. If you have any difficulty, go back and review the steps for that type of calculation. When you feel ready to evaluate your learning, take the first posttest. Check your answers. An acceptable score as indicated on the posttest signifies that you are ready for the next chapter. An unacceptable score signifies a need for further study before taking the second posttest.
A percent is a third way of showing a fractional relationship. Fractions, decimals, and percents can all be converted from one form to the others. Conversions of fractions and decimals are discussed in Chapter 2. A percent indicates a value equal to the number of hundredths. Therefore when a percent is written as a fraction, the denominator is always 100. The number beside the percent sign (%) becomes the numerator.
ALERT
CHANGING A FRACTION TO A PERCENT
EXAMPLE 1:
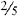
CHANGING A DECIMAL TO A PERCENT
CHANGING A PERCENT TO A FRACTION
2. Write the remaining number as the fraction’s numerator.
3. Write 100 as the denominator. (The denominator will always be 100.)
CHANGING A PERCENT TO A DECIMAL
2. Divide the remaining number by 100 (by moving the decimal point two places to the left).
3. Express the quotient as a decimal. Place a zero before the decimal if there are no whole numbers.
CHANGING A PERCENT CONTAINING A FRACTION TO A DECIMAL
2. Change the mixed number to an improper fraction.
3. Divide by 100. Remember, the denominator of all whole numbers is 1.
5. Divide the numerator by the denominator, expressing the quotient as a decimal.
