Decimals

LEARNING OBJECTIVES

On completion of the materials provided in this chapter, you will be able to perform computations accurately by mastering the following mathematical concepts:

1 Reading and writing decimal numbers

2 Determining the value of decimal fractions

3 Adding, subtracting, multiplying, and dividing decimals

4 Rounding decimal fractions to an indicated place value

5 Multiplying and dividing decimals by 10 or a power of 10

6 Multiplying and dividing decimals by 0.1 or a multiple of 0.1

7 Converting a decimal fraction to a proper fraction

8 Converting a proper fraction to a decimal fraction

Study the introductory material for decimals. The processes for the calculation of decimal problems are listed in steps. Memorize the steps for each calculation before beginning the work sheet. Complete the work sheet at the end of this chapter, which provides for extensive practice in the manipulation of decimals. Check your answers. If you have difficulties, go back and review the steps for that type of calculation. When you feel ready to evaluate your learning, take the first posttest. Check your answers. An acceptable score as indicated on the posttest signifies that you are ready for the next chapter. An unacceptable score signifies a need for further study before you take the second posttest.

Decimals are used in the metric system of measurement. Nurses use the metric system in the calculation of drug dosages. Therefore it is essential for nurses to be able to manipulate decimals easily and accurately.

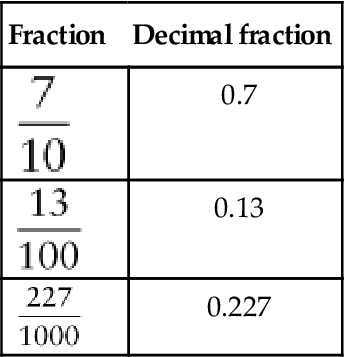
Each decimal fraction consists of a numerator that is expressed in numerals; a decimal point placed so that it designates the value of the denominator; and the denominator, which is understood to be 10 or some power of 10. In writing a decimal fraction, always place a zero to the left of the decimal point so that the decimal point can readily be seen. The omission of the zero may result in a critical medication error. Some examples are as follows:

Fraction	Decimal fraction
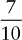710	0.7
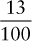13100	0.13
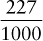2271000	0.227

Decimal numbers include an integer (or whole number), a decimal point, and a decimal fraction. The value of the combined integer and decimal fraction is determined by the placement of the decimal point. Whole numbers are written to the left of the decimal point, and decimal fractions to the right. Figure 2-1 illustrates the place occupied by the numeral that has the value indicated.

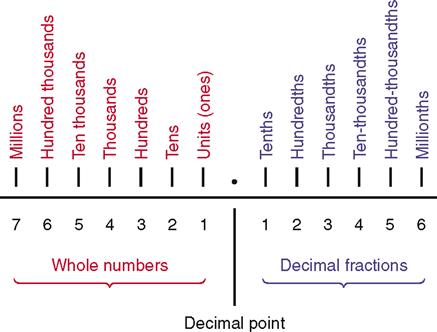
READING DECIMAL NUMBERS

The reading of a decimal number is determined by the place value of the integers and decimal fractions.

1. Read the whole number.

2. Read the decimal point as “and” or “point.”

3. Read the decimal fraction.

EXAMPLES:	0.4	four tenths
	0.86	eighty-six hundredths
	3.659	three and six hundred fifty-nine thousandths
	182.0012	one hundred eighty-two and twelve ten-thousandths
	9.47735	nine and forty-seven thousand seven hundred thirty-five hundred-thousandths

DETERMINING THE VALUES OF DECIMAL FRACTIONS

1. Place the numbers in a vertical column with the decimal points in a vertical line.

2. Add zeros on the right in the decimal fractions to make columns even.

3. The largest number in a column to the right of the decimal point has the greatest value.

4. If two numbers in a column are of equal value, examine the next column to the right, and so on.

5. The smallest number in the column to the right of the decimal point has the least value. If two numbers in the first column are of equal value, examine the second column to the right, and so on.

EXAMPLE 1: Of the following fractions (0.623, 0.841, 0.0096, 0.432), which has the greatest value? the least value?

0.841 has the greatest value; 0.0096 has the least value.

NOTE: In mixed numbers the values of both the integer and the fraction are considered.

EXAMPLE 2: Which decimal number (0.4, 0.25, 1.2, 1.002) has the greatest value? the least value?

1.2 has the greatest value; 0.25 has the least value.

ADDITION AND SUBTRACTION OF DECIMALS

1. Write the numerals in a vertical column with the decimal points in a straight line.

2. Add zeros as needed to complete the columns.

3. Add or subtract each column as indicated by the symbol.

4. Place the decimal point in the sum or difference directly below the decimal points in the column.

5. Place a zero to the left of the decimal point in a decimal fraction.

EXAMPLE 1: Add: 14.8 + 6.29 + 3.028

14.8006.290+ 3.02824.118¯

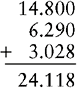
EXAMPLE 2: Subtract: 5.163 − 4.98

5.163– 4.9800.183¯

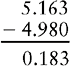
MULTIPLICATION OF DECIMALS

1. Place the shorter group of numbers under the longer group of numbers.

2. Multiply.

3. Add the number of places to the right of the decimal point in the multiplicand and the multiplier (i.e., the numbers being multiplied). The sum determines the placement of the decimal point within the product.

4. Count from right to left the value of the sum and place the decimal point.

EXAMPLE 1: 0.19 × 0.24

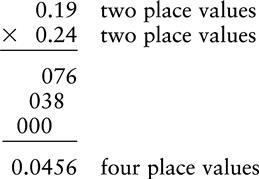
EXAMPLE 2: 0.459 × 0.52

EXAMPLE 3: 8.265 × 4.36

EXAMPLE 4: 160.41 × 3.527

Multiplying a Decimal by 10 or a Power of 10 (100, 1000, 10,000, 100,000)

1. Move the decimal point to the right the same number of places as there are zeros in the multiplier.

2. Zeros may be added as indicated.

EXAMPLE 1:

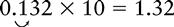
EXAMPLE 2:

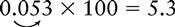
EXAMPLE 3:

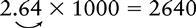
EXAMPLE 4:

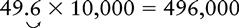
Multiplying a Whole Number or Decimal by 0.1 or a Multiple of 0.1 (0.01, 0.001, 0.0001, 0.00001)

1. Move the decimal point to the left the same number of spaces as there are numbers to the right of the decimal point in the multiplier.

2. Zeros may be added as indicated.

EXAMPLE 1:

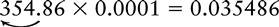
EXAMPLE 2:

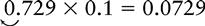
EXAMPLE 3:

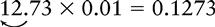
EXAMPLE 4:

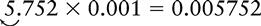
ROUNDING A DECIMAL FRACTION

1. Find the number to the right of the place value desired.

2. If the number is 5, 6, 7, 8, or 9, add 1 to the number in the place value desired and drop the rest of the numbers.

3. If the number is 0, 1, 2, 3, or 4, remove all numbers to the right of the desired place value.

EXAMPLE 1: Round the following decimal fractions to the nearest tenth.

a.	0.268
	0.2)68	6 is the number to the right of the tenth place. Therefore 1 should be added to the number 2 and the 68 dropped.
	0.3	correct answer
b.	4.374
	4.3)74	7 is the number to the right of the tenth place. Therefore 1 should be added to the number 3 and the 74 dropped.
	4.4	correct answer
c.	5.723
	5.7)23	2 is the number to the right of the tenth place. Therefore all numbers to the right of the tenth place should be removed.
	5.7	correct answer

EXAMPLE 2: Round the following decimal fractions to the nearest hundredth.

a.	0.876
	0.87)6	6 is the number to the right of the hundredths place. Therefore 1 should be added to the number 7 and the 6 dropped.
	0.88	correct answer
b.	2.3249
	2.32)49	4 is the number to the right of the hundredths place. Therefore all numbers to the right of the hundredths place should be removed.
	2.32	correct answer

EXAMPLE 3: Round the following decimal fractions to the nearest thousandth.

a.	3.1325
	3.132)5	5 is the number to the right of the thousandths place. Therefore 1 should be added to the number 2 and the 5 dropped.
	3.133	correct answer
b.	0.4674
	0.467)4	4 is the number to the right of the thousandths place. Therefore all numbers to the right of the thousandths place should be removed.
	0.467	correct answer

Rounding numbers helps to estimate values, compare values, have more realistic and workable numbers, and spot errors. Decimal fractions may be rounded to any designated place value.