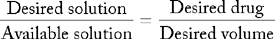COMMUNITY
Objectives
• Identify the problems with conversion of metric to household measure.
• Name the components of a solution.
• List three methods of preparing a solution.
• Describe three ways solutions are labeled.
• State the formula used for calculating a solution of a desired concentration.
• State the formula used for calculating a weaker solution from a stronger solution.
• Identify the types of devices used for home infusion therapy.
• Determine daily fluid intake for an adult and a febrile adult.
• Describe the importance of body mass index (BMI) in health assessment.
Although the metric system is widespread in the clinical area, the home setting generally does not have the devices of metric measure. This becomes a problem when liquid medication is prescribed in metric measure for the home patient. Measuring spoons and syringes with metric measurements are available in pharmacies, and families should be encouraged to purchase them. If metric devices are not available, the community nurse should be able to assist the patient in converting metric to household measure.
Preparation of solutions in the home setting may involve conversion between the metric and household systems. Solutions used in the home setting can be used for oral fluid replacement, topical application, irrigation, or disinfection. Although the majority of the solutions are commercially available, solutions that can be prepared in the home can be effective and less costly than the premixed items.
When commercially prepared drugs are too concentrated for the patient’s use and must be diluted, it is necessary to calculate the strength of the solution to meet the therapeutic need as prescribed by the physician. Knowledge of solution preparation and metric-household conversion can be a useful skill for the community nurse.
METRIC TO HOUSEHOLD CONVERSION
When changing from metric to household measure, use the ounce from the apothecary system as an intermediary, because there is no clear conversion between the two systems.
The conversion factors for volume are:
Ounces to milliliters: multiply ounces × 29.57 or 30
Milliliters to ounces: multiply milliliters × 0.034
The conversion factors for weight are:
Ounces to grams: multiply ounces × 28.35
Grams to ounces: multiply grams × 0.035
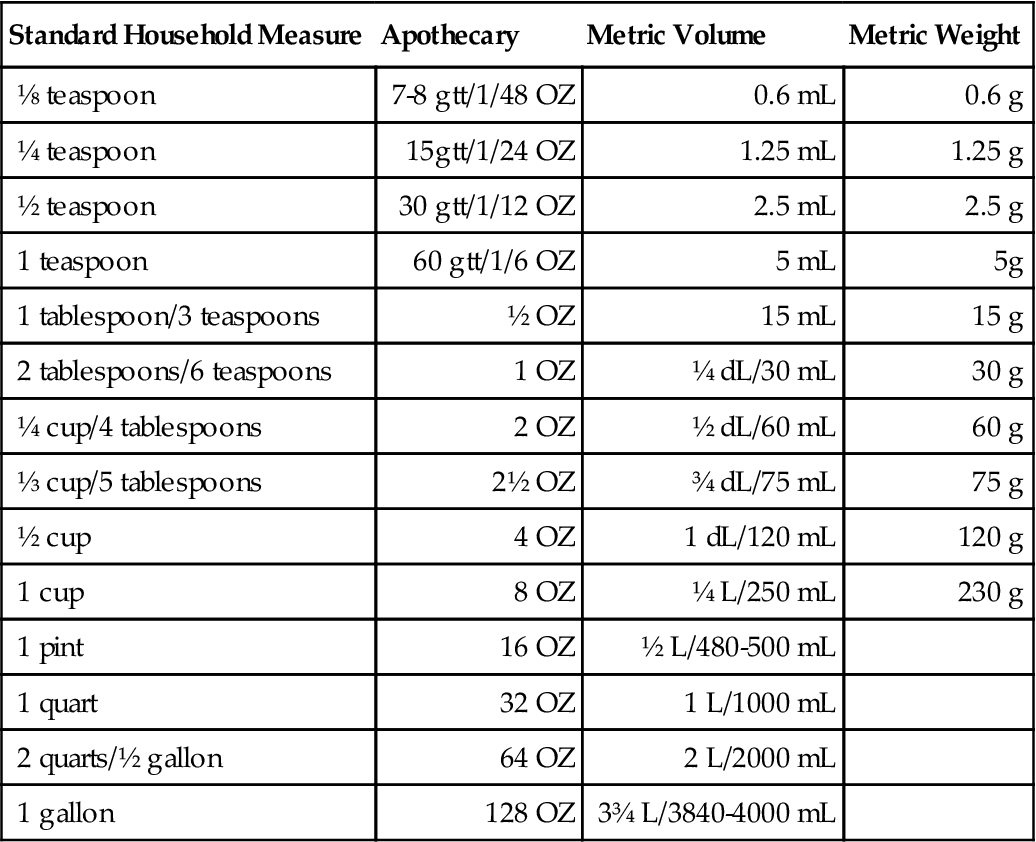
Note that weight and volume measures differ in the metric system. The properties of crystals, powders, and other solids account for the differences more so than the liquids. Also, as liquid measures increase in volume, there are greater discrepancies between metric and standard household measure. Table 15-1 shows the current approximate equivalents. Deciliters and liters are also included with the volume measurements. These terms will be seen more commonly as the use of the metric system increases. Although conversion charts are helpful guides, a metric measuring device would be optimal for drug administration. Standard household measuring devices should be used instead of tableware if a metric device is not available.
TABLE 15-1
Household to Metric Conversions (Approximate)
| Standard Household Measure | Apothecary | Metric Volume | Metric Weight |
| ⅛ teaspoon | 7-8 gtt/1/48 OZ | 0.6 mL | 0.6 g |
| ¼ teaspoon | 15gtt/1/24 OZ | 1.25 mL | 1.25 g |
| ½ teaspoon | 30 gtt/1/12 OZ | 2.5 mL | 2.5 g |
| 1 teaspoon | 60 gtt/1/6 OZ | 5 mL | 5g |
| 1 tablespoon/3 teaspoons | ½ OZ | 15 mL | 15 g |
| 2 tablespoons/6 teaspoons | 1 OZ | ¼ dL/30 mL | 30 g |
| ¼ cup/4 tablespoons | 2 OZ | ½ dL/60 mL | 60 g |
| ⅓ cup/5 tablespoons | 2½ OZ | ¾ dL/75 mL | 75 g |
| ½ cup | 4 OZ | 1 dL/120 mL | 120 g |
| 1 cup | 8 OZ | ¼ L/250 mL | 230 g |
| 1 pint | 16 OZ | ½ L/480-500 mL | |
| 1 quart | 32 OZ | 1 L/1000 mL | |
| 2 quarts/½ gallon | 64 OZ | 2 L/2000 mL | |
| 1 gallon | 128 OZ | 3¾ L/3840-4000 mL |
PRACTICE PROBLEMS 
I METRIC TO HOUSEHOLD CONVERSION
Answers can be found on pages 331 to 333.
Use Table 15-1 to convert metric to household measure.
1. Bismuth subsalicylate 15 mL every hour up to 120 mL in 24 hr.
_________________________________
2. Ceclor 5 mL four times per day.
_________________________________
3. Tylenol elixir 1.25 mL every 6 hours as necessary for temperature greater than 102° F.
_________________________________
4. Maalox 30 mL after meals and at bedtime.
_________________________________
5. Neo-Calglucon 7.5 mL three times per day.
_________________________________
6. Gani-Tuss NR liquid 10 mL, q6h, prn.
_________________________________
7. Castor oil 60 mL at bedtime.
_________________________________
Use Table 15-1 for conversions.
8. Metamucil 5 g in 1 glass of water every morning.
_________________________________
9. Dilantin-30 pediatric suspension 10 mL twice per day.
_________________________________
10. Homemade pediatric electrolyte solution:
H2O 1 L, boiled ____________________
Sugar 30 g ____________________
Salt 1.5 g ____________________
Lite salt 2.5 g ____________________
Baking soda 2.5 g ____________________
H2O 500 mL boiled ____________________
Table salt 5 mL ____________________
Baking soda 5 mL ____________________
12. Magic mouthwash:
Benadryl 50 mg/10 mL ____________________
Maalox 10 mL ____________________
13. Gastrointestinal cocktail for gastric upset:
Belladonna/phenobarbital elixir, 10 mL ____________________
Maalox, 30 mL ____________________
PREPARING A SOLUTION OF A DESIRED CONCENTRATION
All solutions contain a solute (drug) and a solvent (liquid). Solutions can be mixed three different ways:
1. Weight to weight: Involves mixing the weight of a given solute with the weight of a given liquid.
EXAMPLE
5 g sugar with 100 g H2O
This type of preparation is used in the pharmaceutical setting and is the most accurate. Scales for weight to weight preparation are not usually found in the home setting.
EXAMPLE
10 g of salt in 1 L of H2O
or
⅓ oz of salt in 1 qt of H2O
Again, a scale is needed for this preparation.
3. Volume to volume: Means that a given volume of solution is mixed with a given volume of solution.
EXAMPLE
10 mL of hydrogen peroxide 3% in 1 dL H2O
or
2 T of hydrogen peroxide 3% in ½ c H2O
Preparation of solutions volume to volume is commonly used in both clinical and home settings.
After a solution is prepared, the strength can be expressed numerically in three different ways:
With a ratio, the first number is the solute and the second number is the solvent. In a fraction, the numerator is the solid and the denominator is the liquid. A solution labeled by percentage indicates the amount of solute in 100 mL of liquid. All pharmaceutically prepared solutions use the metric system, and the ratio, fraction, and percentages are interpreted in grams per milliliter.
Changing a Ratio to Fractions and Percentages
Change a ratio to a percentage or a fraction by setting up a proportion using the following variables:
Known drug : Known volume :: Desired drug : Desired volume
A proportion can also be set up like a fraction:
REMEMBEREXAMPLE
Change acetic acid 1 : 20 to a percentage
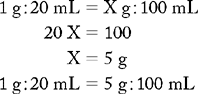
Note: In percentage, the volume of liquid is 100 mL.
The ratio can be expressed as a fraction, 5 g/100 mL, or as a percentage, 5%. Another method of changing a ratio to a percentage involves finding a multiple of 100 for volume (denominator), then multiplying both terms by that multiple.
PRACTICE PROBLEMS 
II PREPARING A SOLUTION OF A DESIRED CONCENTRATION
Answers can be found on pages 333 and 334.
Change the following ratios to fractions and percentages.
1. 4 : 1
2. 2 : 1
3. 1 : 50
4. 1 : 3
5. 1 : 1000
6. 1 : 10,000
7. 1 : 4
8. 1 : 5000
9. 1 : 200
10. 1 : 10
In the previous problems, grams per milliliter is the unit of measure used for preparing solutions. Scales for measuring grams are rarely found in the clinical area or the home environment. Volume (in milliliters) is the common measurement of drugs for administration. Drugs that are powders, crystals, or liquids are measured in graduated measuring cups with metric, apothecary, or household units. The milliliter, although a volume measure, can be substituted for a gram, a measure of mass, because at 4° C, 1 mL of water weighs 1 g. Mass and volume differ with the type of substance; thus grams and milliliters are not exact equivalents in all instances, but they can be accepted as approximate values for preparation of solutions.
Calculating a Solution From a Ratio
To obtain a solution from a ratio, use the proportion or fraction method.
EXAMPLES
PROBLEM 1: Prepare 500 mL of a 1 : 100 vinegar-water solution for a vaginal douche.
Known drug : Known volume :: Desired drug : Desired volume
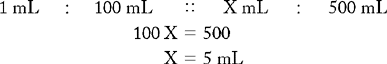
or
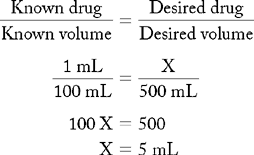
ANSWER: 5 mL of vinegar added to 500 mL of water is a 1 : 100 vinegar-water solution.
Note: Five milliliters did not increase the volume of the solution by a large amount. When volume and volume solutions are mixed, the total amount of desired volume should not be exceeded. Therefore it is important to determine the volume of desired drug first, then remove that volume from the appropriate amount of solvent (solution). When mixing the solution, begin with the desired drug and add the premeasured solvent. This process ensures that the solution has an accurate concentration.
PROBLEM 2: Prepare 100 mL of a 1 : 4 hydrogen peroxide 3% and normal saline mouthwash.
Known drug : Known volume :: Desired drug : Desired volume
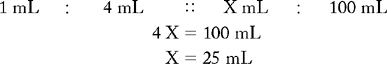
25 mL of hydrogen peroxide 3% is the amount of desired drug. To calculate the amount of normal saline, use the following formula:
Desired volume − Desired drug = Desired solvent
100 mL − 25 mL = 75 mL
ANSWER: 75 mL of saline and 25 mL of hydrogen peroxide 3% make 100 mL of a 1 : 4 mouthwash.
Calculating a Solution From a Percentage
To obtain a solution from a percentage, use the same formula with either the proportion or fraction method.
EXAMPLE
Prepare 1000 mL of a 0.9% NaCl solution.
Known drug : Known volume :: Desired drug : Desired volume
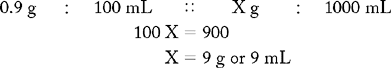
ANSWER: 9 g or 9 mL of NaCl in 1000 mL makes a 0.9% NaCl solution.
PREPARING A WEAKER SOLUTION FROM A STRONGER SOLUTION
When a situation requires the preparation of a weaker solution from a stronger solution, the amount of desired drug must be determined. The known variables are the desired solution, the available or on-hand solution, and the desired volume. The formula can be set up with the strength of the solutions expressed in either ratio or percentage. The proportion method or the fractional method can be used to solve the problem. The first ratio or fraction, the desired solution (weaker solution), is the numerator, and the available or on-hand solution (stronger solution) is the denominator.
Desired solution : Available solution :: Desired drug : Desired volume
