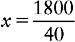Oral Dosages
LEARNING OBJECTIVES
On completion of the materials provided in this chapter, you will be able to perform computations accurately by mastering the following mathematical concepts:
1 Converting all measures within the problem to equivalent measures in one system of measurement
3 Using a proportion to solve problems of oral dosages of medications measured in milliequivalents
4 Using the stated formula as an alternative method of solving oral-drug dosage problems
Oral drugs are preferred for administration of medications because they are easy to take and convenient for the patient. Oral medications are absorbed through the gastrointestinal tract; therefore the skin is not interrupted. Oral medications may be more economical because the production cost is usually lower than for other forms of medication.
Oral medications are absorbed primarily in the small intestine. Because of the differences in absorption factors, they might not be as effective as other forms of medication. Some oral medications are irritating to the alimentary canal and must be given with meals or a snack. Others may be harmful to the teeth and should be taken through a straw or feeding tube.
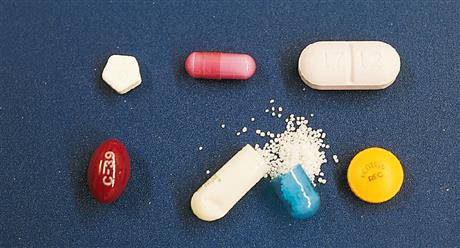
Oral medications are supplied in a variety of forms (Figure 13-1). The most common form is a tablet. Tablets come in many colors, sizes, and shapes. A tablet is produced from a drug powder. The tablet may be grooved for ease in administering only a fraction of the whole tablet. Some tablets are scored into halves, and others are divided into fourths (Figure 13-2).
If a patient has difficulty swallowing pills, some pills may be crushed using a mortar and pestle or a device that is specifically made for crushing pills (Figure 13-3). Before crushing any medication in pill form, verify the medication can be crushed. Some medications, such as those that are enteric coated or sustained or extended release, should not be crushed.
ALERTOral medications may also be supplied in capsule form. A capsule is a hard or soft gelatin that houses a powder, liquid, or granular form of a specific medicine(s). Capsules are produced in a variety of sizes and colors (Figure 13-4). Capsules cannot be divided or crushed.
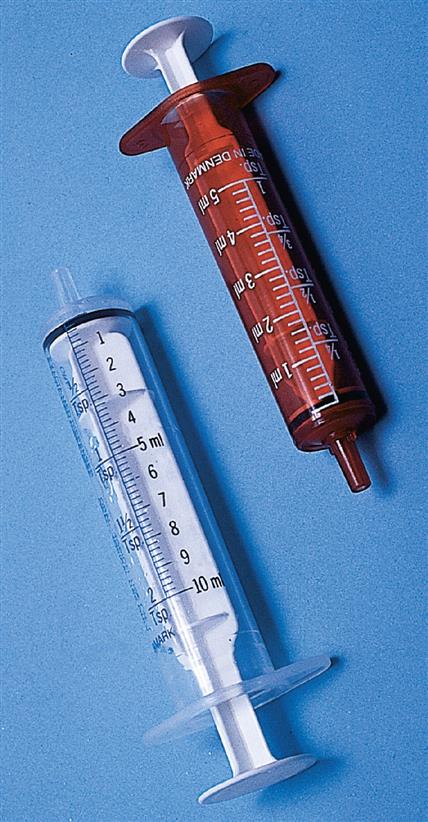
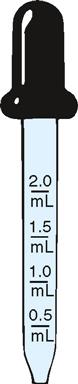
Oral medications may also be administered in liquid form such as an elixir or an oral suspension. Oral liquid medications can be measured with a medication cup, oral syringe (syringe without the needle attached), or dropper (Figures 13-5 to 13-7).
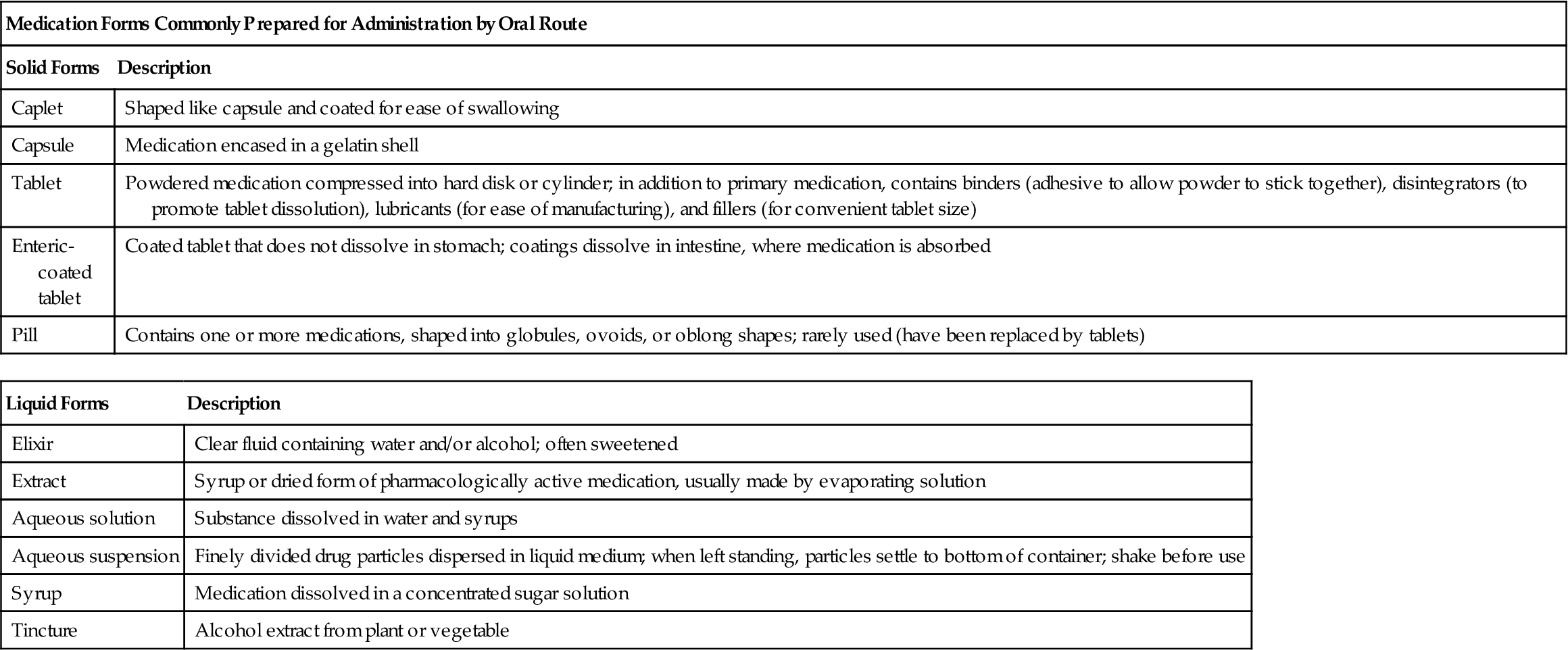
ALERTTable 13-1 describes the forms of a variety of medications.
TABLE 13-1
| Medication Forms Commonly Prepared for Administration by Oral Route | |
| Solid Forms | Description |
| Caplet | Shaped like capsule and coated for ease of swallowing |
| Capsule | Medication encased in a gelatin shell |
| Tablet | Powdered medication compressed into hard disk or cylinder; in addition to primary medication, contains binders (adhesive to allow powder to stick together), disintegrators (to promote tablet dissolution), lubricants (for ease of manufacturing), and fillers (for convenient tablet size) |
| Enteric-coated tablet | Coated tablet that does not dissolve in stomach; coatings dissolve in intestine, where medication is absorbed |
| Pill | Contains one or more medications, shaped into globules, ovoids, or oblong shapes; rarely used (have been replaced by tablets) |
| Liquid Forms | Description |
| Elixir | Clear fluid containing water and/or alcohol; often sweetened |
| Extract | Syrup or dried form of pharmacologically active medication, usually made by evaporating solution |
| Aqueous solution | Substance dissolved in water and syrups |
| Aqueous suspension | Finely divided drug particles dispersed in liquid medium; when left standing, particles settle to bottom of container; shake before use |
| Syrup | Medication dissolved in a concentrated sugar solution |
| Tincture | Alcohol extract from plant or vegetable |
Modified from Potter PA, Perry AG: Fundamentals of nursing, ed 7, St Louis, 2009, Mosby.
Oral Dosages Involving Capsules and Tablets: Proportion Method
Sometimes the physician’s order is in one strength of measurement, and the drug is supplied in another strength of measurement. It is therefore necessary to convert one of the measurements so that they are both in the same strength of measurement. After this is done, another proportion will be written to calculate the actual drug dosage.
EXAMPLE 1: The physician orders ampicillin 0.5 g po four times a day. The drug is supplied in 250-mg capsules. How many capsules will the nurse administer? _______
The physician’s order is in grams and the drug is supplied in milligrams. The order and the supplied drug must be in the same strength of measurement because only two different abbreviations can be used in each proportion. Therefore first convert 0.5 g to milligrams.
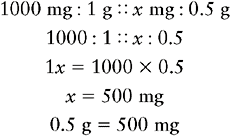
Now that the order and the supplied drug are in the same strength of measurement, a proportion may be written to calculate the amount of the drug to be given.
b. 250 mg : 1 capsule ::_______ mg : _______ capsule
250 mg : 1 capsule :: 500 mg : x capsule
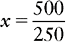
e. x = 2 capsules. Therefore to give 0.5 g of the medication, the nurse will administer 2 capsules.
How many capsules will be given in 1 day? _______
The drug is to be given four times a day.
b. 2 capsules : 1 dose :: _______ capsules : _______ dose
2 capsules : 1 dose :: x capsules : 4 doses
EXAMPLE 2: The physician orders aspirin 975 mg po four times a day. Aspirin 325-mg tablets are available. How many tablets will the nurse administer? _______
a. On the left side of the proportion place what you know or have available. In this example, each tablet contains 325 mg. So the left side of the proportion is
1 tablet : 325 mg ::
b. The right side of the proportion is determined by the physician’s order and the abbreviations used on the left side of the proportion. Only two different abbreviations may be used in a single proportion. The abbreviations must be in the same position on the right as they are on the left.
1 tablet : 325 mg :: _______ tablet : _______ mg
In the example, the physician has ordered 975 mg.
1 tablet : 325 mg :: _______ tablet : 975 mg
We need to find the number of tablets to be given, so we use the symbol x to represent the unknown. Therefore the full proportion is
1 tablet : 325 mg :: x tablet : 975 mg
c. Rewrite the proportion without using the abbreviations.
1 : 325 :: x : 975
d. Solve for x.
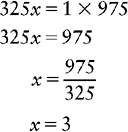
e. Label your answer, as determined by the abbreviation placed next to x in the original proportion.
975 mg = 3 tablets
Oral Dosages Involving Liquids: Proportion Method
EXAMPLE 1: The physician orders phenobarbital 45 mg po two times a day. Phenobarbital elixir, 20 mg/5 mL, is available. How many milliliters will the nurse administer? _______
A proportion can be written to calculate the actual amount of the drug to be administered.
b. 20 mg : 5 mL :: _______ mg : _______ mL
20 mg : 5 mL :: 45 mg : x mL
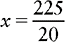
e. x = 11.25 mL. Therefore 11.25 mL is the amount of each individual dose twice a day.
EXAMPLE 2: The physician orders Thorazine 20 mg po q4 h. The drug is available in 120 mL bottles of Thorazine syrup containing 10 mg/5 mL. How many milliliters will the nurse administer? _______ How many doses are available in 120 mL? _______
b. 10 mg : 5 mL :: _______ mg : _______ mL
10 mg : 5 mL :: 20 mg : x mL
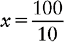
e. x = 10 mL. Therefore 10 mL is the amount of each individual dose q4 h.
A proportion can be written to calculate the number of doses in a 120 mL bottle.
b. 10 mL : 1 dose :: _______ mL : _______ dose
10 mL : 1 dose :: 120 mL : x dose
d. 10x = 120
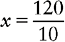
e. x = 12 doses. Therefore each iv oz bottle contains 12 doses.
Oral Dosages Involving Milliequivalents: Proportion Method
EXAMPLE: The physician orders potassium chloride (KCl) 60 mEq three times a day with meals. KCl 40 mEq/30 mL is available. How many milliliters will the nurse administer? _______
A milliequivalent is the number of grams of a solute contained in 1 mL of a normal solution. The milliequivalent is used in a drug dosage proportion, the same as a form of measurement in the apothecary or metric system.
Alternative Formula Method of Oral Drug Dosage Calculation
A formula has been used for many years in the calculation of drug dosages by nurses. The formula method may be the method that some students learned first in an earlier nursing role (e.g., for a nurse who was a licensed practical nurse or who is returning to work in the area of direct patient care). If this is the case and the student accurately uses the formula method, we do not recommend changing to the proportion method. However, if calculations have frequently been difficult or incorrect, we recommend using the proportion method. Remember, choose the method that you feel is best for you and consistently use the chosen method. We do not recommend switching back and forth between the formula method and the proportion method. When you use the formula method, the desired and available amounts must be in the same units of measurement.
D represents the desired amount of the medication that has been ordered by the physician.
A represents the strength of the medication that is available.
Qrepresents the quantity or amount of the medication that contains the available strength.
ALERTWhen the medication is a solid such as a tablet, capsule, or caplet, the quantity will always be 1. If the medication is in liquid form, the number will vary. Remember from the math review, the denominator of a whole number is always one: 
, etc.
x represents the dose that is unknown.
This formula can be read as:
Desired over (or divided by) available multiplied by the quantity available equals x, or the amount to be given to the patient.
Oral Dosages Involving Capsules and Tablets: Alternative Formula
If the physician’s order is in one strength of measurement and the drug is supplied in another strength of measurement, it will still be necessary to convert one of the measurements so that both are expressed in the same system. After this is done, the formula may be used to calculate the drug dose to be administered.
EXAMPLE 1: The physician orders ampicillin 0.5 g po four times a day. The drug is supplied in 250-mg capsules. How many capsules will the nurse administer? _______
The physician’s order is expressed in grams and the drug is supplied in milligrams. Therefore convert the order to milligrams as outlined in Chapter 8.
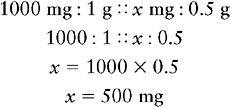
Now the numbers may be filled into the formula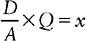 
a. The desired amount of ampicillin is 500 mg. The available amount or strength f ampicillin supplied is 250 mg.
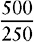
b. The quantity available is in capsule form, or 1.
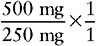
c. Rewrite the problem with the abbreviations cancelled.
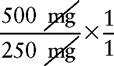
d. Solve for x.
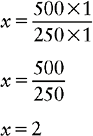
e. Label your answer as determined by the quantity.
500 mg = 2 capsules
EXAMPLE 2: The physician orders aspirin 975 mg po four times a day. Aspirin tablets 325 mg are available. How many tablets will the nurse administer? _______
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
