 Dimensional Analysis and the Calculation of Drug Dosages
Dimensional Analysis and the Calculation of Drug Dosages
LEARNING OBJECTIVES
On completion of the materials provided in this chapter, you will be able to perform computations accurately by mastering the following mathematical concepts:
1 Using the dimensional analysis format to solve oral dosage problems
2 Using the dimensional analysis format to solve parenteral dosage problems
3 Using the dimensional analysis format to solve problems of intravenous flow rate in drops per minute
6 Using the dimensional analysis format to solve pediatric and obstetrical dosage problems
![]() Dimensional analysis is another format for setting up problems to calculate drug dosages. The advantage of dimensional analysis is that only one equation is needed. This is true even if the information supplied indicates a need to convert to like units before setting up the proportion to perform the actual calculation of the amount of medication to be given to the patient.
Dimensional analysis is another format for setting up problems to calculate drug dosages. The advantage of dimensional analysis is that only one equation is needed. This is true even if the information supplied indicates a need to convert to like units before setting up the proportion to perform the actual calculation of the amount of medication to be given to the patient.
EXAMPLE: The order states Augmentin 500 mg po daily. The drug is supplied in 250-mg tablets. How many tablets will the nurse administer?
a. On the left side of the equation, place the name or abbreviation of the drug form of x, or what you are solving for.
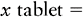

b. On the right side of the equation, place the available information related to the measurement or abbreviation that was placed on the left side. In this example that is tablet. This information is placed in the equation as a common fraction; match the appropriate abbreviation or measurement. Thus the abbreviation that matches the x quantity must be placed in the numerator. We also know from the problem that each tablet contains 250 mg of Augmentin. This information is the denominator of our fraction.
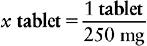
c. Next, find the information that matches the measurement or abbreviation used in the denominator of the fraction you created. In this example mg is in the denominator and our order is for 500 mg. Therefore the full proportion is
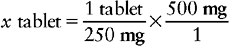
d. Now cancel out the like abbreviations on the right side of the equation. If you have set up the problem correctly, the remaining measurement or abbreviation should match that used on the left side of the equation. You are now ready to solve for x.
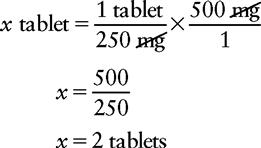
As stated earlier, the advantage of this method is not having to convert into like systems of measurement as would be required if the usual proportion method were used. With dimensional analysis, remember that only one equation is necessary. Let’s look at another example.
EXAMPLE: The order states Kantrex 400 mg IM q12 h. The drug is supplied as 0.5 g/2 mL. How many milliliters will the nurse administer?
a. On the left side of the equation, place the name or abbreviation of the drug form for which you are solving, or x.
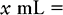
b. On the right side of the equation, place the available information related to the measurement or abbreviation that was placed on the left side. In this example that is mL. This information is placed in the equation as part of a fraction; match the appropriate abbreviation. Remember that the abbreviation that matches the x quantity must be placed in the numerator. We know from the problem that each 2 mL contains 0.5 g of Kantrex.
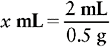
c. Because the order is for 400 mg and the medication is supplied to us as 0.5 g/2 mL, a conversion would normally be required. However, with the dimensional analysis method, an additional fraction is added on the right side of the equation. From information supplied in earlier chapters, we know that 1 g equals 1000 mg. This information is then placed in the equation next in the form of the fraction 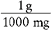 . Note that the abbreviation or measurement in the numerator of this fraction must match the abbreviation or measurement in the denominator of the immediate previous fraction. The equation now looks like
. Note that the abbreviation or measurement in the numerator of this fraction must match the abbreviation or measurement in the denominator of the immediate previous fraction. The equation now looks like
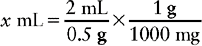
d. Next, place the amount of drug ordered in the equation. Note that this will once again match the measurement or abbreviation of the denominator of the fraction immediately before. In this example, that is 400 mg. Therefore the full equation is
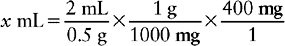
e. For the final step, cancel out the like abbreviations on the right side of the equation. If the equation has been set up correctly, the remaining abbreviation should match that located on the left side. Now solve for x.
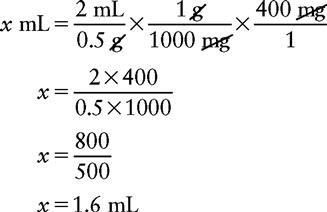
The answer to the problem is 1.6 mL.
USING DIMENSIONAL ANALYSIS TO CALCULATE IV FLOW RATES
The dimensional analysis method can also be used to calculate intravenous (IV) flow rates. The following formulas demonstrate how to calculate drops per minute (gtt/min) and milliliters per hour (mL/h). These formulas can be used to solve IV problems in Chapters 16 and 17.
EXAMPLE 1: A patient has an order for enalaprilat 0.625 mg daily IVPB (intravenous piggyback). The enalaprilat is diluted in 50 mL of D5W (dextrose 5% in water) and is to be infused over 20 minutes. The tubing drop factor is 60 gtt/mL. At what rate, in drops per minute, should the IVPB be programmed?
a. On the left side of the equation, place what you are solving for.
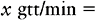
b. On the right side of the equation, place the available information related to the measurement that was placed on the left side of the equation. In this example the measurement we are solving for is gtt/min. We will deal with the numerator portion of our answer first: the gtt. This information is placed in the equation as a common fraction; match the appropriate measurement. Thus the abbreviation that matches the x quantity must be placed in the numerator. We also know from the problem that each milliliter contains 60 gtt. This information is the denominator of our fraction.
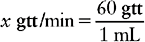
c. Next, find the information that matches the measurement used in the denominator of the fraction you created. In this example mL is in the denominator and our order is for 50 mL. We also know that the enalaprilat should be infused over 20 minutes. The equation now looks like
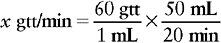
d. Then cancel out the like abbreviations on the right side of the equation. If you have set up the problem correctly, the remaining measurement should match the measurement on the left side of the equation. Now solve for x.

Therefore the nurse will regulate the IVPB for 150 gtt/min, and the enalaprilat will be infused over 20 minutes.
EXAMPLE 2: A postoperative patient has an order for 200 mL 0.9% normal saline solution (NS) over 2 hours. The tubing drop factor is 10 gtt/mL. At what rate, in drops per minute, should the NS be infused?
a. On the left side of the equation, place what you are solving for.
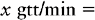
b. On the right side of the equation, place the available information related to the measurement that was placed on the left side of the equation. In this example, the measurement we are solving for is gtt/min. We will deal with the numerator portion of our answer first: the gtt. This information is placed in the equation as a common fraction; match the appropriate measurement. Thus the abbreviation that matches the x quantity must be placed in the numerator on the right side of the equation. We know from the problem that each milliliter contains 10 gtt. This information is the denominator of our fraction.
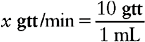
c. Next, find the information that matches the measurement used in the denominator of the fraction you created. In this example mL is in the denominator and our order is for 200 mL. We also know that this 200 mL should be infused over 2 hours. The equation now looks like
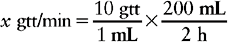
d. Now, we need to solve for minutes, but the order is for hours. So, the equivalent of 1 h : 60 min must be added to the equation as a fraction. The equation would now look like this.
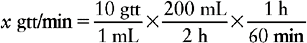
e. Then cancel out the abbreviations on the right side of the equation. If you have set up the problem correctly, the remaining measurement should match that used on the left side of the equation. Now solve for x.

Therefore the nurse will regulate the IV for 17 gtt/min, and 200 mL of 0.9% NS will be infused over 2 hours.
EXAMPLE 3: A patient has an order for regular insulin IV at a rate of 5 units/h. The concentration is insulin 100 units/100 mL 0.9% NS. At what rate, in milliliters per hour, should the IV pump be programmed?
a. On the left side of the equation, place what you are solving for.
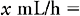
b. On the right side of the equation, place the available information related to the measurement that was placed on the left side of the equation. In this example the measurement we are solving for is mL/h. We will deal with the numerator portion of our answer first: the mL. This information is placed in the equation as a common fraction; match the appropriate measurement. Thus the abbreviation that matches the x quantity must be placed in the numerator on the right side of the equation. We know from the problem that 100 units of insulin are diluted in the 100 mL; this information becomes the denominator of our fraction.
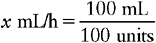
c. Next, find the information that matches the measurement used in the denominator of the fraction you created. In this example, units is the denominator and our order is for 5 units/h. The equation now looks like
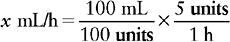
d. Then cancel out the abbreviations on the right side of the equation. If you have set up the problem correctly, the remaining measurement should match the measurement on the left side of the equation. Now solve for x.
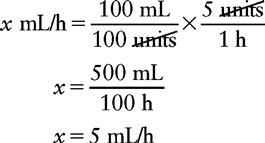
Therefore the nurse will program the IV pump for 5 mL/h, and the insulin will be infused at a rate of 5 units/h.
EXAMPLE 4: A patient with a femoral thrombus has an order for heparin IV at 1200 units/h. The concentration is heparin 20,000 units in 250 mL of D5W. At what rate, in milliliters per hour, should the IV pump be programmed?
a. On the left side of the equation, place what you are solving for.
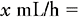
b. On the right side of the equation, place the available information related to the measurement that was placed on the left side of the equation. In this example the measurement we are solving for is mL/h. We will deal with the numerator portion of our answer first: the mL. This information is placed in the equation as a common fraction; match the appropriate measurement. Thus the abbreviation that matches the x quantity must be placed in the numerator. We also know from the problem that there are 20,000 units of heparin in 250 mL. This information becomes the denominator of our fraction.
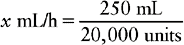
c. Next, find the information that matches the measurement used in the denominator of the fraction you created. In this example, units is the denominator. The order is for 1200 units/h. The equation now looks like
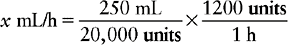
d. Then cancel out the like abbreviations on the right side of the equation. If you have set up the problem correctly, the remaining measurement should match the measurement on the left side of the equation. Now solve for x.

Therefore the nurse will program the IV pump for 15 mL/h, and the heparin will be infused at a rate of 1200 units/h.
EXAMPLE 5: The order is to start a heparin infusion using the heparin protocol. The patient’s weight is 143 lb. Using the weight-based heparin protocol example below, the nurse needs to do two calculations: the heparin bolus and the rate, in milliliters per hour, at which to program the IV pump.
Weight-Based Heparin Protocol (Example)
An order is received to begin IV heparin per facility protocol. The patient’s weight is 143 lb.
| PTT Result | Heparin Dosing |
| <35 | Bolus 70 units/kg and increase drip by 4 units/kg/h |
| 35–54 | Bolus 35 units/kg and increase drip by 3 units/kg/h |
| 55–85 | Therapeutic—no change |
| 86–100 | Decrease drip by 2 units/kg/h |
| >100 | Hold infusion 1 hour; decrease drip by 3 units/kg/h, then restart drip |
Bolus.
The protocol calls for 70 units/kg, rounded to the nearest hundreds.
a. On the left side of the equation, place what you are solving for.
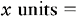
b. On the right side of the equation, place the available information related to the measurement that was placed on the left side of the equation. In this example the measurement we are solving for is units. We will deal with the numerator portion of our answer first: the units. This information is placed in the equation as a common fraction, matching the appropriate measurement. Thus the abbreviation that matches the x quantity must be placed in the numerator. We know from the protocol that 70 units/kg is needed. This information becomes the denominator of our fraction.
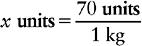
c. Next, find the information that matches the measurement used in the denominator of the fraction you created. In this example, kg is the denominator. The conversion of 1 kg = 2.2 lb is used as the next fraction. The equation now looks like
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


