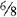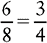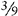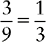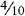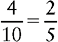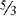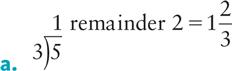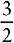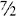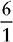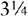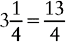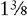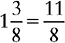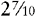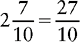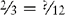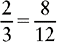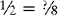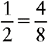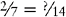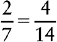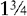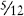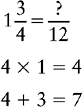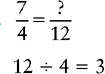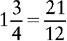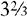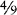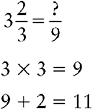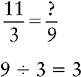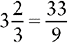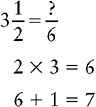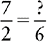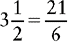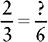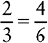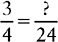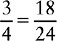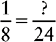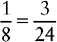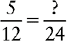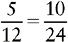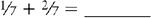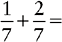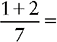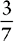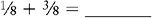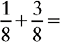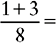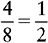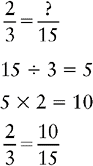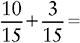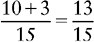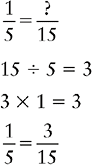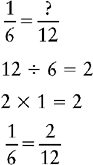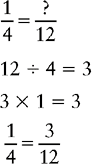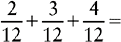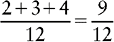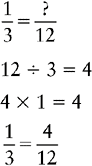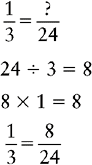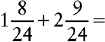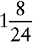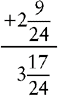Fractions
Fractions
LEARNING OBJECTIVES
On completion of the materials provided in this chapter, you will be able to perform computations accurately by mastering the following mathematical concepts:
1 Changing an improper fraction to a mixed number
2 Changing a mixed number to an improper fraction
3 Changing a fraction to an equivalent fraction with the lowest common denominator
4 Changing a mixed number to an equivalent fraction with the lowest common denominator
7 Multiplying fractions and mixed numbers
8 Dividing fractions and mixed numbers
![]() Study the introductory material for fractions. The processes for the calculation of fraction problems are listed in steps. Memorize the steps for each type of calculation before beginning the work sheet. Complete the work sheet at the end of this chapter, which provides extensive practice in the manipulation of fractions. Check your answers. If you have difficulties, go back and review the steps for that type of calculation. When you feel ready to evaluate your learning, take the first posttest. Check your answers. An acceptable score (number of answers correct) as indicated on the posttest signifies that you are ready for the next chapter. An unacceptable score signifies a need for further study before you take the second posttest.
Study the introductory material for fractions. The processes for the calculation of fraction problems are listed in steps. Memorize the steps for each type of calculation before beginning the work sheet. Complete the work sheet at the end of this chapter, which provides extensive practice in the manipulation of fractions. Check your answers. If you have difficulties, go back and review the steps for that type of calculation. When you feel ready to evaluate your learning, take the first posttest. Check your answers. An acceptable score (number of answers correct) as indicated on the posttest signifies that you are ready for the next chapter. An unacceptable score signifies a need for further study before you take the second posttest.
A fraction indicates the number of equal parts of a whole. For example, ¾ means three of four equal parts.
The denominator indicates the number of parts into which a whole has been divided. The denominator is the number below the fraction line. The numerator designates the number of parts that you have of a divided whole. It is the number above the fraction line. The line also indicates division to be performed and can be read as “divided by.” The example ¾, or three fourths, can therefore be read as “three divided by four.” In other words the numerator is “divided by” the denominator. The numerator is the dividend, and the denominator is the divisor. When numbers are multiplied, the answer is the product. When numbers are divided, the answer is the quotient.
A fraction can often be expressed in smaller numbers without any change in its real value. This is what is meant by the direction “Reduce to lowest terms.” The reduction is accomplished by dividing both numerator and denominator by the same number.
There are several different types of fractions. A proper fraction is one in which the numerator is smaller than the denominator. A proper fraction is sometimes called a common or simple fraction.
EXAMPLES: 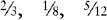
An improper fraction is a fraction in which the numerator is larger than or equal to the denominator.
EXAMPLES: 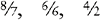
A complex fraction is one that contains a fraction in its numerator, its denominator, or both.
EXAMPLES: 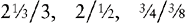
Sometimes a fraction is seen in conjunction with a whole number. This combination is called a mixed number.
EXAMPLES: 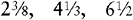
IMPROPER FRACTIONS
Changing an Improper Fraction to a Mixed Number
When an improper fraction is reduced, it will always result in a mixed number or a whole number.
Changing a Mixed Number to an Improper Fraction
1. Multiply the denominator of the fraction by the whole number.
2. Add the product to the numerator of the fraction.
LOWEST COMMON DENOMINATOR
Computations are facilitated when the lowest common denominator is used. The term lowest common denominator is defined as the smallest whole number that can be divided evenly by all denominators within the problem.
When trying to determine the lowest common denominator, first observe whether one of the denominators in the problem is evenly divisible by each of the other denominators. If so, this will be the lowest common denominator for the problem.
EXAMPLE 1: ⅔ and 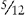
You find that 12 is evenly divisible by 3; therefore 12 is the lowest common denominator.
EXAMPLE 2: ½ and ⅜
You find that 8 is evenly divisible by 2; therefore 8 is the lowest common denominator.
EXAMPLE 3:
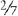
and 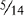 and
and 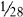
You find that 28 is evenly divisible by 7 and 14; therefore 28 is the lowest common denominator.
Changing a Fraction to an Equivalent Fraction with the Lowest Common Denominator
1. Divide the lowest common denominator by the denominator of the fraction to be changed.
2. Multiply the quotient by the numerator of the fraction to be changed.
Changing a Mixed Number to an Equivalent Fraction with the Lowest Common Denominator
1. Change the mixed number to an improper fraction.
2. Divide the lowest common denominator by the denominator of the fraction.
3. Multiply the quotient by the numerator of the improper fraction.
If one of the denominators in the problem is not the lowest common denominator for all, you must look further. One suggestion is to multiply two of the denominators together and if possible use that number as the lowest common denominator.
Example: 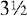 and
and 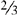
Multiply the two denominators: 2 × 3 = 6
Another method is to multiply one of the denominators by 2, 3, or 4. Determine whether the resulting number can be used as a common denominator.
Example: 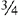 and
and 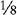 and
and 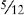
Multiply the denominator 8 by 3: 8 × 3 = 24
ADDITION OF FRACTIONS
Addition of Fractions Having the Same Denominator
Addition of Fractions with Unlike Denominators
1. Change the fractions to equivalent fractions with the lowest common denominator.
3. Place the sum over the lowest common denominator.
EXAMPLE 1: 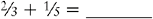
To find the lowest common denominator, multiply the two denominators together.
3 × 5 = 15
Change each fraction to an equivalent fraction with 15 as the denominator.
EXAMPLE 2: 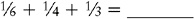
To find a common denominator, try multiplying two of the denominators together and check to see whether that number is divisible by the other denominator.
4 × 3 = 12
Is 12 divisible by the other denominator, 6? The answer is YES.
Addition of Fractions Involving Whole Numbers and Unlike Denominators
1. Change the fractions to equivalent fractions with the lowest common denominator.
3. Place the sum over the lowest common denominator.
5. Write the reduced fraction next to the sum of the whole numbers.
EXAMPLE 1: 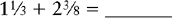
To find the lowest common denominator, multiply the two denominators together.
3 × 8 = 24
Change the fractions 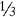 and
and 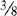 to equivalent fractions with 24 as their denominators.
to equivalent fractions with 24 as their denominators.
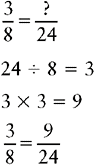
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree