Figure 1 Schematic diagram of the viral dynamics models. (a) Classic model of viral dynamics. Target cells (T) are supplied at constant rate s and die at rate d per day. These cells become infected at rate β V per day. Free virions are produced from infected cells (I) at a rate p and are removed at a rate c. Infected cells are lost at a rate δ. (b) Acute virus infection model modified from the classic model. Target cell regeneration and death are not included. Infected cells were split into two classes, I1 and I2, where virus production initially undergoes an eclipse phase (k).
For influenza virus, the classic model has been modified to provide a more accurate representation of the infection dynamics. First, since influenza dynamics are rapid (lasting approximately 7-10 days), including regeneration and natural death of these target cells, which have longer time scales, has little effect on the dynamics [2, 38] and are typically excluded (s = 0, d = 0).
Second, the eclipse phase, i.e., the time it takes for viral production to begin after initially becoming infected, is missing from the classic model, although it has been added in later HIV models [45, 67]. The eclipse phase can be incorporated into models by including a second class of infected cells (I1) that are in the eclipse phase and cannot yet produce virus. In one class of models, cells in the eclipse phase (I1) transition to a productive state (I2) at rate k. This model, shown schematically in Fig. 1(b) and given by the equations in Box 1, simplifies matters and assumes that no cell death occurs before the initiation of virus production. In other classes of influenza models, the time spent in the eclipse phase is described by either a fixed or distributed delay [6, 46, 68], as has been done in HIV modeling [45, 67].
In general, including the eclipse phase does not change the model behavior and may not be statistically justifiable since the number of parameters is increased, but parameter estimates made by fitting the model to data enter more biologically realistic ranges [2, 6] and growth kinetics are more accurate [90] when taking into account these dynamics.
Third, the virus lost from entry into cells is typically excluded in viral kinetic models since this is usually a negligible amount of virus compared with the amount lost by other processes such as phagocytosis and mucociliary clearance. However, in cell culture, this is not the case [6, 68]. Furthermore, particularly in influenza infection, it is typical to measure only infectious virus. Therefore, loss of viral infectivity can be modeled as clearance of infectious virus. Parameters estimated using viral titers from infection of MDCK cells in vitro suggested that the loss of viral infectivity (c = 0.1 h−1) is much smaller than the loss of virus from cell entry (β T0 = 5.0 h−1) [6]. Thus, in this system where only infectious virus was modeled, an extra term (−γ TV) was added to the virus equation in Box 1, such that dV/dt = pI−cV−γ TV, since the viral entry dynamics could not be neglected [6]. Here, γ is the adsorption rate of virus, which we expect to be greater than the infection rate (β) since it may take more than one infectious viral particle to infect a single cell. Even though model fits were better, γ was less than β when estimated by data fitting [6]. The issue of why γ was less than β has yet to be fully resolved, but one possible explanation proposed by Beauchemin et al. [6] was that the number of infectious virions counted by the plaque assay, V, was an underestimate of the true number, Vreal. They showed that changing variables from V to Vreal = ζ V, with ζ < 1, and rewriting the model equations could resolve the paradox. Other solutions, although non-mechanistic, are to enforce β T0 < c and exclude the γ TV term [89], fix the value of γ/β [68] or constrain it to be ≥ 1.
Characterizing influenza infection kinetics using data fitting and models to estimate parameters is a useful technique, but obtaining an accurate model in which all parameters are identifiable is challenging. The target cell limited model (Box 1) has 4 equations and 7 parameters (β, p, c, δ, k, the initial viral inoculum, V0, and the initial target cell density, T0) for which nonlinear least squares or the maximum likelihood analog are the most frequently used methods to establish parameter values. However, not all parameters are identifiable [82, 89, 93] and it has been necessary to fix some parameters (e.g., the eclipse phase parameter, k) or restrict the ratios of parameters (e.g., β T0 < c) to ensure they take on biologically relevant values. Additionally, it has been shown that the initial target cell density, T0, and the rate of virus production, p, appear in the model solution only as a product, pT0, and, hence, only one of these parameters can be estimated [65, 93]. Most often, T0 is fixed and p is estimated [2, 6, 39, 82, 89].
Another difficulty in estimating parameters characterizing influenza infection is the variety of experimental systems and virus strains used in various studies. For example, the data used to parameterize models has come from humans infected with influenza virus strains A/Hong Kong/123/77 (H1N1) [2, 70] or A/Texas/91 (H1N1) [39, 42], Welsh ponies infected with influenza A/equine/Newmarket/79 (H3N8) virus [78, 82], BALB/cJ mice infected with influenza A/Puerto Rico/8/34 (H1N1) virus [38, 49, 89] or a variant expressing the 1918 PB1-F2 protein [89], C57BL/6 mice infected with influenza A/Hong Kong/X31 (H3N2) virus [65], and Madin-Darby canine-kidney (MDCK) cells infected in vitro with influenza A/Albany/1/98 (H3N2) virus [6], influenza A/Puerto Rico/8/34 (H1N1) [85], influenza A/Wisconsin/67/2005 (H3N2) [85], or equine influenza virus strain A/Equi 2 (H3N8), Newmarket 1/93 [68]. The existing data suggest that parameter estimates drawn from certain systems are strain and cell type specific and cannot be generalized to all influenza infections (Table 1).
Table 1 Estimates of parameter values for influenza infection.
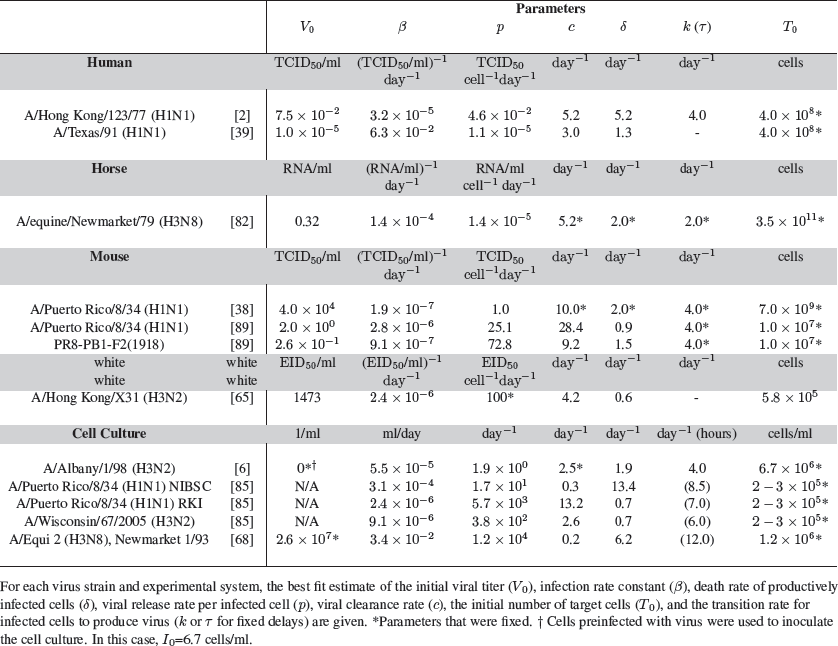
The estimates of the infected cell lifespan are an example of this, where estimated values have varied depending on the type of data used and the strain of influenza. Cells in the productively infected state were estimated to have a lifespan of 5 hours in an experimental human infection [2], 13 hours in cell culture [6], and 16 hours for one influenza strain and 27 hours for another in mice [89]. Furthermore, in addition to possibly inducing cell death at different rates, influenza viruses (e.g., H1N1 versus H3N2) may differ in their rates of infection. The rate of virus production may also be different depending on the virus strain but also dependent on the cell type (e.g., MDCK cells versus A549 cells).
To aid in the identification of model parameters, analysis of the model equations has been useful (Box 1). Approximate solutions of Eq. (2) in Box 1 have elucidated the contributions of parameters to the initial viral growth rate and the decay rate of viral titers in the recovery phase [90]. Early in the infection, many of the parameters influence the dynamics, but viral decay is described by the infected cell death rate (δ) when it is much smaller than the rates of viral clearance (c) and eclipse phase transition (k) [90], as it is thought to be in vivo. In vitro, however, the immune response is absent and, hence, c may be much less than δ. This implies that, in such circumstances, viral decay is determined by the rate of viral clearance. From this, a value for δ (or c, in vitro) can be easily found by fitting a line to the decay of log viral titers in the recovery phase (typically beginning on 3 days post-inoculation), which reduces the number of parameter that need to be fitted. In vivo, quantitative measurements of the number of infected cells or the number of dead cells as a result of virus infection are difficult to obtain, and thus direct measurements of δ have not been obtained. However, some data does exist [49, 82, 85], and a few models have incorporated this type of data [38, 82, 85].
Furthermore, studying influenza dynamics in vitro has strengthened the understanding of viral production and clearance rates in the absence of an immune response. For example, the loss of infectious virus due to an infectivity loss was examined by incubating virus in cell culture media in the absence of cells and then evaluating the amount of infectious virus, measured by plaque assay, at various times. The amount of infectious virus decayed with time yielding an estimated viral infectivity half-life of 6.6 hours for influenza A/Albany/1/98 (H3N2) virus [6]. The clearance rate of infectious virus within a host can be expected to have an even shorter half-life, on average, since virus can be lost by cell entry and by immune-mediated mechanisms. For instance, in a murine model, the infectious virus half-life of influenza A/Puerto Rico/8/34 (H1N1) was 0.6 hours [89], which is substantially shorter than 6.6 hours.
Understanding the differences in pathogenicity of virus strains is an important aspect of influenza biology. Modeling influenza kinetics using the target cell limited model (Box 1) played an integral role in teasing apart the differences and potential mechanisms of a virulent influenza strain compared to a less pathogenic one [89]. In this case, an analysis was done of two influenza viruses that differed only in the PB1-F2 protein that they express. In one virus, the PB1-F2 was from the 1918 pandemic strain A/Brevig Mission/1/1918 (H1N1), while the other was the natural PB1-F2 of influenza A/Puerto Rico/8/34 (H1N1). The PB1-F2 protein is thought to increase inflammation and contribute to viral virulence [17, 62, 63, 109], and the variant carrying the 1918 PB1-F2 was expected to be more virulent [17, 63]. Fitting the model showed a significant difference in the kinetics of the two infections with the most notable influences of PB1-F2 on the viral replication rate (p) and the infected cell death rate (δ) [89].
3 Virus Control By Host Immune Responses
The limitation in viral growth that defines the viral titer peak may be controlled by innate immunity rather than by loss of target cells. Furthermore, adaptive immunity contributes to the eradication of virus [21], as virus can persist for long periods in immunocompromised hosts [26]. Using both in vitro and in vivo experimental systems can provide information about the efficiency of a host’s immune response at controlling influenza infection. However, only comparing viral titer measurements from these systems gives no indication about adaptive immune responses versus innate immune responses. Therefore, quantitative measurements of immunological components are necessary to evaluate individual contributions of the host response.
One difficulty of this approach, however, is the limited availability of such kinetic data in coordination with viral titers. Early models focused on developing a comprehensive view of immune response dynamics but did not incorporate sufficient data to validate the models [11, 37]. More recent modeling efforts have examined these host responses by using data from experimental infections in horses [78, 82] and in mice [7, 38, 60, 65].
3.1 Innate Immune Control
During primary influenza infection, the release of proinflammatory cytokines by antigen presenting cells and the infected lung epithelium initiates the innate immune response [53]. In particular, the type I interferons, interferon alpha and beta (IFN-α and IFN-β), are thought to play a major role in limiting viral replication by interacting with susceptible cells and rendering them “resistant” to infection [30, 49, 83]. This effectively prevents virus from establishing a productive infection within the cell and is thought to allow time for the adaptive immune system to respond and clear the virus [77]. These antiviral effects have been explored with Eq. (2) in Box 1 [2, 13, 38] and in a more complicated extension of this model [82].
Interferon levels begin to rise shortly after virus becomes detectable and correlate well with viral replication [49]. The time lag that occurs between the initiation of an influenza infection and the appearance of IFN has been modeled with the equation dF/dt = η I(t−τ)−α F, where η is the IFN production rate, α is the IFN decay rate, and τ is a time delay (Box 2). Because IFN can reduce viral replication in an infected cell [72], the rate of viral production in the presence of IFN has been modeled as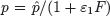 
. The rate that cells in the eclipse phase begin virus production (k) may also be altered and was accounted for by redefining this parameter, 
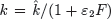. The efficiency of these interferon effects is reflected by the parameters ε1and ε2[2].
Estimating these parameters is difficult since obtaining well characterized IFN kinetics in the lungs is challenging, especially in human infections. Thus, incorporating the dynamics of IFN into Eq. (2) in Box 1, which increases the number of parameters, could not be statistically justified in one model given the lack of supporting data [2]. However, including these dynamics could explain a potential biphasic increase or plateau of titers during the viral decay phase [2].
Because IFN-α is produced not only by infected cells but also by cells such as plasmacytoid dendritic cells [16], it was assumed in one model (Box 2) that the rate of IFN production was proportional to the amount of free virus rather than to infected cells [38]. Interestingly, comparing this model to IFN measurements from influenza infected mice [49], it was necessary to enforce a decrease in interferon concentration on day 5 by setting the production rate to zero (i.e., ω = 0) since this cytokine disappeared even when viral titers remained at high levels [38].
Another way to model the effects of IFN is to explicitly consider cells that enter an antiviral state, in which they are refractory to infection (Box 2) [13, 37, 82]. Simultaneously fitting the model to viral titers, IFN concentrations and death of infected cells in horses experimentally infected with the equine influenza [78] suggested that the contribution of the innate immune response in viral control outweighed the effects of target cell limitation in this system [82].
3.2 Adaptive Immune Control
Adaptive immune responses to influenza, involving B cells and T cells, are thought to dictate the decrease and eventual clearance of virus [21, 100], particularly in individuals previously exposed to influenza [15]. In addition to their antiviral effects, type I interferons stimulate effector cells, such as natural killer (NK) cells and cytotoxic T lymphocytes (CTLs), that destroy influenza infected epithelial cells [21, 83]. Virus specific B cells and plasma cells, on the other hand, produce antibodies that can neutralize the virus and reduce its infectivity (anti-HA antibodies) or reduce viral levels (anti-NA antibodies) [52], possibly by reducing virus release from infected cells.
Including components of the adaptive response such as these to influenza models increases their complexity and requires sufficient data to support such a model. However, even with well characterized data, a large number of model parameters may not be identifiable. In this case, simulating the equations with biologically plausible parameter values may be the only option [11, 37, 60].
Less complicated models can still be useful for teasing apart the effects that adaptive immunity has on viral kinetics (Box 3). In several instances, modeling efforts have been focused on the CTL response [7, 13, 38, 101], which in one study in mice was shown to begin increasing around day 5 after inoculation, to peak around 10 day and to return to a baseline level around 20 days postinfection [65]. Each of the models suggested that the CTL response plays an important role in complete viral clearance.
While CTLs have effects on infected cells, which in turn affects virus concentrations, antibodies have direct effects on free virus. The antibody response is important to consider since efficient removal of virus without damaging the respiratory tract, as with CTL killing of cells, is ideal. In mice, virus-specific antibodies begin increasing around 5 days after inoculation which is followed by a peak in IgM level around 8-10 days and in IgG levels around 25 days and eventual decay [65]. The dynamics of antibody (A), as measured in mice infected with A/Puerto Rico/8/34 (H1N1) [49], were modeled in combination with the effects of the innate response (i.e., IFN) (Box 3). While the model fit the data well, replacing the antibody response with the CTL response resulted in fits that were equally as good [38]. Therefore, additional data would be necessary to distinguish the contributions of these two responses to viral clearance.
Detailed models of the immune response to influenza virus infection highlight three important components: the effects of interferon (i.e., the removal of target cells available for infection), the effects of cellular immunity (i.e., the killing of infected cells), and the effects of antibodies (i.e., the effective virus concentration is reduced) [37, 60, 65]. Incorporation of the dynamics of antigen presenting cells, such as dendritic cells, has also been done [37, 60]. Only one study, however, used quantitative data from a large number of mice, in which virus, CD8 T cells, and antibody (both IgG and IgM) were all measured, and combined with a detailed model. By doing so, model parameters could be estimated and the effects of the CTL response on reducing infected cell half-life and of antibody on increasing infectious virus loss were quantitatively assessed [65].
4 Influenza Kinetics in Response to Antivirals
Influenza antiviral agents are used therapeutically and prophylactically to prevent individuals who are exposed from acquiring the virus, to reduce the severity of infection, and to limit virus transmission to others who are susceptible. Two classes of antiviral drugs are currently approved for treatment of influenza [25]: the adamantanes (amantadine and rimantadine) and the neuraminidase inhibitors (NIs, oseltamivir and zanamivir) (reviewed in references [19, 35, 51]). Viral resistance is prevalent with use of both classes of drugs, although resistance to the adamantanes is more common particularly when used therapeutically rather than prophylactically [40].
Adamantanes reduce the ability of the virus to infect cells by blocking the activity of the M2 protein ion channel which has been modeled by reducing β by (1-ε(t)), where ε(t) represents the effectiveness of the drug and may not be constant due to the pharmacokinetic and pharmacodynamic effects of the drug (Box 4). Fitting Eq. (2) in Box 1 to viral titers obtained in the presence of amantadine resulted in the estimate that this drug may at best only be 74% efficacious in vitro with the low efficacy most likely due to rapid development of drug resistance [6].
To analyze the effects of giving the antiviral drug oseltamivir, which blocks the release of virus from infected cells, the viral production rate (p) is altered (Box 4). With p multiplied by (1-εNI), where εNIis the efficacy of the drug (e.g., εNI = 1 implies 100% effectiveness), the model was fitted to viral titers in patients post-treatment (the antiviral was administered early (26 or 32 hours postinoculation) or late (50 hours postinoculation) [42]). With this data, the drug was estimated to stop 97-99% of viral production in humans infected with influenza A/Hong Kong/123/77 (H1N1) virus [2].
The emergence of drug-resistant virus can alter infection dynamics. To model this scenario (Box 4), the virus population can be split into two classes: virions that are sensitive to the drug (Vs) and virions that are resistant to the drug (Vr). Mutations leading to resistant virus typically have an associated fitness cost such that either virus production (p) is lowered or the infection rate (β) is lowered [39]. Examining the properties of resistant strains, such as the differences in viral titers and in plaque size and growth velocity, has also been done using modeling approaches [47]. To do this, Holder and Beauchemin [47] developed a partial differential equation model to examine plaque growth of an NI-resistant strain versus a wild-type strain [47], and the approximate solutions of the target cell limited model [90] were used to examine the viral titers of the resistant and sensitive strains in cell culture [47].
To reduce the effects that drug-resistant mutations have on viral dynamics during treatment, combination therapy can be used. The scenario was examined with a model, which assumed the effects of each drug were additive, and indicated that patients could benefit from treatment with both an amantadine and a neuraminidase inhibitor [60].
In practice, antiviral drugs need to be given within the first 48 hours of infection for maximum results [1]. Indeed, the viral growth phase in influenza infected patients was estimated to last between 30 and 63 hours [90], which was found to be similar in mice [89]. At the point when viral growth significantly slows and a peak is reached, any drug induced changes in the production of virus is predicted to have minimal effects [2].
5 Concluding Remarks
In the last 5 years, new kinetic models for influenza A virus infection driven by quantitative data from experimental infections have been developed. The number of these models has increased significantly in the last 2 years, which has led to an array of models being in the literature with varying complexity [2, 5, 6, 11, 37, 38, 39, 46, 47, 60, 65, 68, 82, 85, 89, 92, 101]. Although controversy still exists about the necessity of including immune responses to describe influenza viral dynamics, kinetic analyses have provided a way to investigate the properties of viral growth and decay and give insights into the control mechanisms involved in combating influenza infection. One general difficulty in developing, validating, and refining within-host influenza models is the lack of available data detailing immune kinetics and epithelial cell pathology, particularly for a natural infection.
An abundance of influenza viral load data exists (e.g., [12, 14, 23, 29, 44, 59, 64, 86, 94, 95, 99, 104, 110]), some of which has been used in modeling studies [2, 6, 38, 39, 46, 47, 65, 68, 82, 85, 89], but analyzing only this type of data may result in exclusion of important dynamics. For example, a recent study comparing influenza infections in aged and adult mice [99] and another comparing influenza strains [62] suggest that lung immunopathology, rather than viral load, is a better indicator of disease severity.
One type of data that is easily attainable and offers a new perspective into the characteristics of an infection is the assigning of a symptom score throughout the infection, which provides insight into how sick a host is. Data of this sort, which has been recorded in mice [99] and in humans (see [12] and references therein), indicates the extent to which cytokines (e.g., TNF-α) are involved in pathogenesis since lung immunopathology is strongly correlated with increased cytokine production [24, 41].
Furthermore, increased viral replication, increased numbers of alveolar macrophages (AMs) and neutrophils, and elevated cytokines and chemokines have all been associated with influenza lethality (reviewed in reference [58]). While some cytokine data does exist (e.g., [3, 18, 20, 27, 34, 41, 43, 56, 55, 78, 88, 99, 103, 106, 108]), these molecules are typically excluded from models because their effects on virus concentrations are indirect. Fewer data sets contain measurements of cells involved in the innate immune response, like macrophages and neutrophils [56, 76, 96, 97, 99, 102, 106], and the effects of these cells have not been incorporated into influenza models. However, these cells may have a crucial role in viral control and clearance, particularly since higher viral titers are observed when AMs and, to a lesser extent, neutrophils are absent [28, 29, 56, 96, 97, 102].
Alveolar macrophages may have another role in influenza infections that could be investigated using a mathematical model. These cells can be infected by influenza virus [8, 71, 76, 79, 84, 61, 105], but it is unclear if the infection is productive (i.e., if infectious virus is produced within and released by AMs) and how much the infection of these cells contribute to the overall dynamics of the infection. That is, it may be of importance to understand whether the virus infection in AMs acts as a sink or a source for free virus.
An additional source of virus, such as from infected AMs, could explain the plateau, or potential second peak, in viral titers observed in some experimental infections during the recovery phase of infection (usually between days 5-7) [9, 10, 22, 36, 41, 50, 69, 70, 80]. One explanation of this phenomena came from a model which suggested that the decreasing interferon response could allow for an increase in viral production [2]. However, other circumstances that allow the virus to undergo a surge in viral titer, such as the virus migrating into new areas of the respiratory tract resulting in an increase in the number of susceptible target cells, could be evaluated with a mathematical model. Besides AMs, other cells in the lung may act as influenza target cells. Furthermore, heterogeneity among lung epithelial cells may make some cells better targets than others. The effects of multiple types of target cells could be investigated with models, as has been done in the field of HIV modeling [75].
The development of influenza kinetic models and the merging of theoretical analyses with experiments has increased significantly over the past several years. So far, these models have used quantitative descriptions of infection kinetics to aid the interpretation of experimental data and improve our understanding of viral control and treatment. The modeling techniques described here focused on viral growth, viral decay, target cell depletion and, to some extent, the immunological involvement. However, several aspects have not yet been addressed. While the dynamics of influenza A virus have been investigated in various studies, the dynamics of influenza B virus [4], which is also an important public health threat, have not been analyzed using kinetic models. The models developed thus far also generally do not incorporate multiple compartments, such as the lung, trachea and nasopharynx [59], that may have interesting dynamical differences. Integrating the extracellular events (e.g., virus production and infected cell death) with the intracellular kinetics (e.g., RNA replication and virus assembly) [87] or the transmission between hosts (e.g., [32, 66]) may give insight into the various aspects of influenza pathogenicity including why some strains cause more inflammation or are more easily transmitted. As the amount of information available continues to increase with new and different data, such as imaging and microarray analysis of gene expression [33, 54, 57, 81], old models should become more refined and new models formulated thus increasing our understanding of influenza infections and how to better treat infected hosts.
6 Acknowledgements
This work was done under the auspices of the U. S. Department of Energy under contract DE-AC52-06NA25396 and supported by NIH contract N0I-AI50020 and grants RR06555 and AI28433.
References
[1] Aoki, F, Macleod, M, Paggiaro, P, Carewicz, O, El Sawy, A, et al. Early administration of oral oseltamivir increases the benefits of influenza treatment. J. Antimicrob. Chemother., 51(1):123–129, 2003.
[2] Baccam, P, Beauchemin, C, Macken, C, Hayden, F, and Perelson, A. Kinetics of influenza A virus infection in humans. J. Virol., 80(15):7590–7599, 2006.
[3] Barbé, F, Atanasova, K, and Van Reeth, K. Cytokines and acute phase proteins associated with acute swine influenza infection in pigs. in press, Vet. J., 2010.
[4] Barroso, L, Treanor, J, Gubareva, L, and Hayden, F. Efficacy and tolerability of the oral neuraminidase inhibitor peramivir in experimental human influenza: randomized, controlled trials for prophylaxis and treatment. Antivir. Ther., 10(8):901–910, 2005.
[5] Beauchemin, C, Samuel, J, and Tuszynski, J. A simple cellular automaton model for influenza A viral infections. J. Theor. Biol., 232(2):223–234, 2005.
[6] Beauchemin, C, McSharry, J, Drusano, G, Nguyen, J, Went, G, et al. Modeling amantadine treatment of influenza A virus in vitro. J. Theor. Biol., 254(2):439–451, 2008.
[7] Belz, G, Wodarz, D, Diaz, G, Nowak, M, and Doherty, P. Compromised influenza virus- specific CD8+-T-cell memory in CD4+-T-cell-deficient mice. J. Virol., 76(23):12388–12393, 2002.
[8] Bender, B and Small Jr, P. Influenza: pathogenesis and host defense. Sem. Resp. Infect., 7(1):38–45, 1992.
[9] Bender, B and Small Jr, P. Heterotypic immune mice lose protection against influenza virus infection with senescence. J. Infect. Dis., 168(4):873–880, 1993.
[10] Bjornson, A, Mellencamp, M, and Schiff, G. Complement is activated in the upper respiratory tract during influenza virus infection. Am. Rev. Respir. Dis., 143(5):1062–1066, 1991.
[11] Bocharov, G and Romanyukha, A. Mathematical model of antiviral immune response III. Influenza A virus infection. J. Theor. Biol., 167(4):323–360, 1994.
[12] Carrat, F, Vergu, E, Ferguson, N, Lemaitre, M, Cauchemez, S, et al. Time lines of infection and disease in human influenza: a review of volunteer challenge studies. Am. J. Epidemiol., 167(7):775–785, 2008.
[13] Chang, D and Young, C. Simple scaling laws for influenza A rise time, duration, and severity. J. Theor. Biol., 246(4):621–635, 2007.
[14] Chen, G, Lamirande, E, Yang, C, Jin, H, Kemble, G, et al. Evaluation of replication and cross-reactive antibody response of H2 influenza subtype viruses in mice and ferrets. in press, J. Virol., 2010.
[15] Clements, M, Betts, R, Tierney, E, and Murphy, B. Serum and nasal wash antibodies associated with resistance to experimental challenge with influenza A wild-type virus. J. Clin. Microbiol., 24(1):157–160, 1986.
[16] Colonna, M, Krug, A, and Cella, M. Interferon-producing cells: on the front line in immune responses against pathogens. Curr. Opin. Immunol., 14(3):373–379, 2002.
[17] Conenello, G, Zamarin, D, Perrone, L, Tumpey, T, and Palese, P. A single mutation in the PB1-F2 of H5N1 (HK/97) and 1918 influenza A viruses contributes to increased virulence. PLoS Pathog., 3(10):e141, 2007.
[18] Conn, C, McClellan, J, Maassab, H, Smitka, C, Majde, J, et al. Cytokines and the acute phase response to influenza virus in mice. Am. J. Physiol. – Reg. I., 268(1):R78–R84, 1995.
[19] De Clercq, E. Antiviral agents active against influenza A viruses. Nat. Rev. Drug Discov., 5(12):1015–1025, 2006.
[20] Desmet, E, Hollenbaugh, J, Sime, P, Wright, T, Topham, D, et al. Mixed Lineage Kinase 3 deficiency delays viral clearance in the lung and is associated with diminished influenza- induced cytopathic effect in infected cells. Virology, 400(2):224–232, 2010.
[21] Doherty, P, Topham, D, Tripp, R, Cardin, R, Brooks, J, et al. Effector CD4+ and CD8+ T-cell mechanisms in the control of respiratory virus infections. Immunol. Rev., 159(1):105–117, 1997.
[22] Douglas Jr, R, Betts, R, Simons, R, Hogan, P, and Roth, F. Evaluation of a topical interferon inducer in experimental influenza infection in volunteers. Antimicrob. Agents Ch., 8(6):684–687, 1975.
[23] Durr, F and Lindh, H. Efficacy of ribavirin against influenza virus in tissue culture and in mice. Ann. N.Y. Acad. Sci., 255:366–371, 2006.
[24] Eccles, R. Understanding the symptoms of the common cold and influenza. Lancet Infect. Dis., 5(11):718–725, 2005.
[25] for Disease Control, C and Prevention. Interim antiviral guidance for 2008–09. http://www.cdc.gov/flu/professionals/antivirals/, 2008.
[26] for Disease Control, C and Prevention. Clinical signs and symptoms of influenza. http://www.cdc.gov/flu/professionals/acip/clinical.htm, 2010.
[27] Fritz, R, Hayden, F, Calfee, D, Cass, L, Peng, A, et al. Nasal cytokine and chemokine responses in experimental influenza A virus infection: results of a placebo-controlled trial of intravenous zanamivir treatment. J. Infect. Dis., 180:586–593, 1999.
[28] Fujisawa, H. Inhibitory role of neutrophils on influenza virus multiplication in the lungs of mice. Microbiol. Immunol., 45(10):679–688, 2001.
[29] Fujisawa, H. Neutrophils play an essential role in cooperation with antibody in both protection against and recovery from pulmonary infection with influenza virus in mice. J. Virol., 82(6):2772–2783, 2008.
[30] García-Sastre, A, Durbin, R, Zheng, H, Palese, P, Gertner, R, et al. The role of interferon in influenza virus tissue tropism. J. Virol., 72(11):8550–8558, 1998.
[31] Genzel, Y, Behrendt, I, König, S, Sann, H, and Reichl, U. Metabolism of MDCK cells during cell growth and influenza virus production in large-scale microcarrier culture. Vaccine, 22(17–18):2202–2208, 2004.
[32] Germann, T, Kadau, K, Longini Jr, I, and Macken, C. Mitigation strategies for pandemic influenza in the United States. Proc. Natl. Acad. Sci. USA, 103(15):5935–5940, 2006.
[33] Gonzalez, S, Lukacs-Kornek, V, Kuligowski, M, Pitcher, L, Degn, S, et al. Capture of influenza by medullary dendritic cells via SIGN-R1 is essential for humoral immunity in draining lymph nodes. Nat. Immunol., 11(5):427–434, 2010.
[34] Grebe, K, Takeda, K, Hickman, H, Bailey, A, Embry, A, et al. Cutting edge: Sympathetic nervous system increases proinflammatory cytokines and exacerbates influenza A virus pathogenesis. J. Immunol., 184(2):540–544, 2010.
[35] Gubareva, L, Kaiser, L, and Hayden, F. Influenza virus neuraminidase inhibitors. The Lancet, 355(9206):827–835, 2000.
[36] Hale, B, Steel, J, Medina, R, Manicassamy, B, Ye, J, et al. Inefficient control of host gene expression by the 2009 pandemic H1N1 influenza A virus NS1 protein. in press, J. Virol., 2010.
[37] Hancioglu, B, Swigon, D, and Clermont, G. A dynamical model of human immune response to influenza A virus infection. J. Theor. Biol., 246(1):70–86, 2007.
[38] Handel, A, Longini, I, and Antia, R. Towards a quantitative understanding of the within-host dynamics of influenza A infections. J. R. Soc. Interface, 7(42):35–47, 2010.
[39] Handel, A, Longini Jr, I, and Antia, R. Neuraminidase inhibitor resistance in influenza: Assessing the danger of its generation and spread. PLoS Comput. Biol., 3(12):e240, 2007.
[40] Hayden, F and Aoki, F. Amantadine, rimantadine, and related agents, antiviral agents. In Yu, V, Meigan, T, and Barriere, S, editors, Antimicrobial therapy and vaccines. Baltimore, MD: Williams and Wilkins, 1999.
[41] Hayden, F, Fritz, R, Lobo, M, Alvord, W, Strober, W, et al. Local and systemic cytokine responses during experimental human influenza A virus infection. J. Clin. Invest., 101(3):643–649, 1998.
[42] Hayden, F, Treanor, J, Betts, R, Lobo, M, Esinhart, J, et al. Safety and efficacy of the neuraminidase inhibitor GG167 in experimental human influenza. J. Am. Med. Assoc., 275(4):295–299, 1996.
[43] Hennet, T, Ziltener, H, Frei, K, and Peterhans, E. A kinetic study of immune mediators in the lungs of mice infected with influenza A virus. J. Immunol., 149(3):932–939, 1992.
[44] Herfst, S, Chutinimitkul, S, Ye, J, de Wit, E, Munster, V, et al. Introduction of virulence markers in PB2 of pandemic swine-origin influenza virus does not result in enhanced virulence or transmission. J. Virol., 84(8):3752–3758, 2010.
[45] Herz, A, Bonhoeffer, S, Anderson, R, May, R, and Nowak, M. Viral dynamics in vivo: limitations on estimates of intracellular delay and virus decay. Proc. Natl. Acad. Sci. USA, 93(14):7247–7251, 1996.
[46] Holder, B and Beauchemin, C. In-host influenza modeling and non-exponential delays. submitted, 2010.
[47] Holder, B, P, S, Liao, L, Abed, Y, Bouhy, X, et al. Assessing fitness of an oseltamivir-resistant seasonal A/H1N1 influenza strain using a mathematical model. submitted, 2010.
[48] Holford, N and Sheiner, L. Pharmacokinetic and pharmacodynamic modeling in vivo. Crit. Rev. Bioeng., 5(4):273–322, 1981.
[49] Iwasaki, T and Nozima, T. Defense mechanisms against primary influenza virus infection in mice: I. The roles of interferon and neutralizing antibodies and thymus dependence of interferon and antibody production. J. Immunol., 118(1):256–263, 1977.
[50] Jao, R, Wheelock, E, and Jackson, G. Production of interferon in volunteers infected with Asian influenza. J. Infect. Dis., 121(4):419–426, 1970.
[51] Jefferson, T, Demicheli, V, Rivetti, D, Jones, M, Di Pietrantonj, C, et al. Antivirals for influenza in healthy adults: systematic review. The Lancet, 367(9507):303–313, 2006.
[52] Johansson, B, Bucher, D, and Kilbourne, E. Purified influenza virus hemagglutinin and neuraminidase are equivalent in stimulation of antibody response but induce contrasting types of immunity to infection. J. Virol., 63(3):1239–1246, 1989.
[53] Julkunen, I, Melén, K, Nyqvist, M, Pirhonen, J, Sareneva, T, et al. Inflammatory responses in influenza A virus infection. Vaccine, 19:S32–S37, 2000.
[54] Kash, J, Tumpey, T, Proll, S, Carter, V, Perwitasari, O, et al. Genomic analysis of increased host immune and cell death responses induced by 1918 influenza virus. Nature, 443(7111):578–581, 2006.
[55] Kaufmann, A, Salentin, R, Meyer, R, Bussfeld, D, Pauligk, C, et al. Defense against influenza A virus infection: essential role of the chemokine system. Immunobiol., 204(5):603–613, 2001.
[56] Kim, H, Lee, Y, Lee, K, Kim, H, Cho, S, et al. Alveolar macrophages are indispensable for controlling influenza viruses in lungs of pigs. J. Virol., 82(9):4265–4274, 2008.
[57] Kobasa, D, Jones, S, Shinya, K, Kash, J, Copps, J, et al. Aberrant innate immune response in lethal infection of macaques with the 1918 influenza virus. Nature, 445(7125):319–323, 2007.
[58] La Gruta, N, Kedzierska, K, Stambas, J, and Doherty, P. A question of self-preservation: immunopathology in influenza virus infection. Immunol. Cell Biol., 85(2):85–92, 2007.
[59] Larson, E, Dominik, J, Rowberg, A, and Higbee, G. Influenza virus population dynamics in the respiratory tract of experimentally infected mice. Infect. Immun., 13(2):438–447, 1976.
[60] Lee, H, Topham, D, Park, S, Hollenbaugh, J, Treanor, J, et al. Simulation and prediction of the adaptive immune response to influenza A virus infection. J. Virol., 83(14):7151–7165, 2009.
[61] Matikainen, S, Pirhonen, J, Miettinen, M, Lehtonen, A, Govenius-Vintola, C, et al. Influenza A and sendai viruses induce differential chemokine gene expression and transcription factor activation in human macrophages. Virology, 276(1):138–147, 2000.
[62] McAuley, J, Chipuk, J, Boyd, K, Van De Velde, N, Green, D, et al. PB1-F2 proteins from H5N1 and 20th century pandemic influenza viruses cause immunopathology. in press, PLoS Pathog., 2010.
[63] McAuley, J, Hornung, F, Boyd, K, Smith, A, McKeon, R, et al. Expression of the 1918 influenza A virus PB1-F2 enhances the pathogenesis of viral and secondary bacterial pneumonia. Cell Host & Microbe, 2(4):240–249, 2007.
[64] McAuley, J, Zhang, K, and McCullers, J. The effects of influenza A virus PB1-F2 protein on polymerase activity are strain specific and do not impact pathogenesis. J. Virol., 84(1):558–564, 2010.
[65] Miao, H, Hollenbaugh, J, Zand, M, Holden-Wiltse, J, Mosmann, T, et al. Quantifying the early immune response and adaptive immune response kinetics in mice infected by influenza A virus. J. Virol., 84(13):6687–6698, 2010.
[66] Mills, C, Robins, J, and Lipsitch, M. Transmissibility of 1918 pandemic influenza. Nature, 432(7019):904–906, 2004.
[67] Mittler, J, Sulzer, B, Neumann, A, and Perelson, A. Influence of delayed viral production on viral dynamics in HIV-1 infected patients. Math. Biosci., 152(2):143–163, 1998.
[68] Möhler, L, Flockerzi, D, Sann, H, and Reichl, U. Mathematical model of influenza A virus production in large-scale microcarrier culture. Biotechnol. Bioeng., 90(1):46–58, 2005.
[69] Murphy, B, Chanock, R, Douglas, R, Betts, R, Waterman, D, et al. Temperature-sensitive mutants of influenza A virus: Evaluation of the Alaska/77-ts-1 A 2 temperature-sensitive recombinant virus in seronegative adult volunteers. Arch. Virol., 65(2):169–173, 1980.
[70] Murphy, B, Rennels, M, Douglas Jr, R, Betts, R, Couch, R, et al. Evaluation of influenza A/Hong Kong/123/77 (H1N1) ts-1A2 and cold-adapted recombinant viruses in seronegative adult volunteers. Infect. Immun., 29:348–355, 1980.
[71] Nain, M, Hinder, F, Gong, J, Schmidt, A, Bender, A, et al. Tumor necrosis factor-alpha production of influenza A virus-infected macrophages and potentiating effect of lipopolysac- charides. J. Immunol., 145(6):1921–1928, 1990.
[72] Neumann, A, Lam, N, Dahari, H, Gretch, D, Wiley, T, et al. Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-therapy. Science, 282(5386):103–107, 1998.
[73] Nowak, M and May, R. Virus Dynamics: Mathematical Principles of Immunology and Virology. Oxford University Press, New York, 2001.
[74] Perelson, A. Modelling viral and immune system dynamics. Nat. Rev. Immunol., 2(1):28–36, 2002.
[75] Perelson, A, Essunger, P, Cao, Y, Vesanen, M, Hurley, A, et al. Decay characteristics of HIV-1-infected compartments during combination therapy. Nature, 387(6629):188–191, 1997.
[76] Perrone, L, Plowden, J, García-Sastre, A, Katz, J, and Tumpey, T. H5N1 and 1918 pandemic influenza virus infection results in early and excessive infiltration of macrophages and neutrophils in the lungs of mice. PLoS Pathog., 4(8):e1000115, 2008.
[77] Price, G, Gaszewska-Mastarlarz, A, and Moskophidis, D. The role of alpha/beta and gamma interferons in development of immunity to influenza A virus in mice. J. Virol., 74(9):3996–4003, 2000.
[78] Quinlivan, M, Nelly, M, Prendergast, M, Breathnach, C, Horohov, D, et al. Pro-inflammatory and antiviral cytokine expression in vaccinated and unvaccinated horses exposed to equine influenza virus. Vaccine, 25(41):7056–7064, 2007.
[79] Reading, P, Whitney, P, Pickett, D, Tate, M, and Brooks, A. Influenza viruses differ in ability to infect macrophages and to induce a local inflammatory response following intraperitoneal injection of mice. Immunol. Cell Biol., pages 1–10, 2010.
[80] Reuman, P, Bernstein, D, Keefer, M, Young, E, Sherwood, J, et al. Efficacy and safety of low dosage amantadine hydrochloride as prophylaxis for influenza A. Antivir. Res., 11(1):27–40, 1989.
[81] Rowe, T, León, A, Crevar, C, Carter, D, Xu, L, et al. Modeling host responses in ferrets during A/California/07/2009 influenza infection. Virology, 401(2):257–265, 2010.
[82] Saenz, R, Quinlivan, M, Elton, D, MacRae, S, Blunden, A, et al. Dynamics of influenza virus infection and pathology. J. Virol., 84(8):3974–3983, 2010.
[83] Santoli, D, Trinchieri, G, and Koprowski, H. Cell-mediated cytotoxicity against virus-infected target cells in humans: II. Interferon induction and activation of natural killer cells. J. Immunol., 121(2):532–538, 1978.
[84] Sareneva, T, Matikainen, S, Kurimoto, M, and Julkunen, I. Influenza A virus-induced IFN-α/β and IL-18 synergistically enhance IFN-γ gene expression in human T cells. J. Immunol., 160(12):6032–6038, 1998.
[85] Schulze-Horsel, J, Schulze, M, Agalaridis, G, Genzel, Y, and Reichl, U. Infection dynamics and virus-induced apoptosis in cell culture-based influenza vaccine production-Flow cytometry and mathematical modeling. Vaccine, 27(20):2712–2722, 2009.
[86] Seo, S, Hoffmann, E, and Webster, R. Lethal H5N1 influenza viruses escape host anti-viral cytokine responses. Nat. Med., 8(9):950–954, 2002.
[87] Sidorenko, Y and Reichl, U. Structured model of influenza virus replication in MDCK cells. Biotechnol. Bioeng., 88(1):1–14, 2004.
[88] Skoner, D, Gentile, D, Patel, A, and Doyle, W. Evidence for cytokine mediation of disease expression in adults experimentally infected with influenza A virus. J. Infect. Dis., 180(1):10–14, 1999.
[89] Smith, A, Adler, F, Mcauley, J, Gutenkunst, R, Ribeiro, R, et al. Effect of 1918 PB1-F2 expression on influenza A virus infection kinetics. submitted, 2010.
[90] Smith, A, Adler, F, and Perelson, A. An accurate two-phase approximate solution to an acute viral infection model. J. Math. Biol., 60(5):711–726, 2010.
[91] Smith, A and Ribeiro, R. Modeling the viral dynamics of influenza A virus infection. Crit. Rev. Immunol., 30(3):291–298, 2010.
[92] Smith, D, Forrest, S, Ackley, D, and Perelson, A. Variable efficacy of repeated annual influenza vaccination. Proc. Natl. Acad. Sci. USA, 96(24):14001–14006, 1999.
[93] Stafford, M, Corey, L, Cao, Y, Daar, E, Ho, D, et al. Modeling plasma virus concentration during primary HIV infection. J. Theor. Biol., 203(3):285–301, 2000.
[94] Szretter, K, Gangappa, S, Belser, J, Zeng, H, Chen, H, et al. Early control of H5N1 influenza virus replication by the type I interferon response in mice. J. Virol., 83(11):5825–5834, 2009.
[95] Tang, X and Chong, K. Histopathology and growth kinetics of influenza viruses (H1N1 and H3N2) in the upper and lower airways of guinea pigs. J. Gen. Virol., 90(2):386–391, 2009.
[96] Tate, M, Brooks, A, and Reading, P. The role of neutrophils in the upper and lower respiratory tract during influenza virus infection of mice. Respir. Res., 9(1):57, 2008.
[97] Tate, M, Deng, Y, Jones, J, Anderson, G, Brooks, A, et al. Neutrophils ameliorate lung injury and the development of severe disease during influenza infection. J. Immunol., 183(11):7441–7450, 2009.
[98] Taubenberger, J and Morens, D. The pathology of influenza virus infections. Ann. Rev. Pathol., 3:499–522, 2008.
[99] Toapanta, F and Ross, T. Impaired immune responses in the lungs of aged mice following influenza infection. Resp. Res., 10(1):112, 2009.
[100] Topham, D and Doherty, P. Clearance of an influenza A virus by CD4+ T cells is inefficient in the absence of B cells. J. Virol., 72(1):882–885, 1998.
[101] Tridane, A and Kuang, Y. Modeling the interaction of cytotoxic T lymphocytes and influenza virus infected epithelial cells. Math. Biosci. Eng., 7(1):171–185, 2010.
[102] Tumpey, T, García-Sastre, A, Taubenberger, J, Palese, P, Swayne, D, et al. Pathogenicity of influenza viruses with genes from the 1918 pandemic virus: functional roles of alveolar macrophages and neutrophils in limiting virus replication and mortality in mice. J. Virol., 79(23):14933–14944, 2005.
[103] Tumpey, T, Lu, X, Morken, T, Zaki, S, and Katz, J. Depletion of lymphocytes and diminished cytokine production in mice infected with a highly virulent influenza A (H5N1) virus isolated from humans. J. Virol., 74(13):6105–6116, 2000.
[104] Van Reeth, K, Gregory, V, Hay, A, and Pensaert, M. Protection against a European H1N2 swine influenza virus in pigs previously infected with H1N1 and/or H3N2 subtypes. Vaccine, 21(13–14):1375–1381, 2003.
[105] Van Riel, D, Munster, V, De Wit, E, Rimmelzwaan, G, Fouchier, R, et al. Human and avian influenza viruses target different cells in the lower respiratory tract of humans and other mammals. Am. J. Pathol., 171(4):1215–1223, 2007.
[106] Wareing, M, Lyon, A, Lu, B, Gerard, C, and Sarawar, S. Chemokine expression during the development and resolution of a pulmonary leukocyte response to influenza A virus infection in mice. J. Leukoc. Biol., 76(4):886–895, 2004.
[107] Wright, P, Neumann, G, and Kawaoka, Y. Orthomyxoviruses. In Knipe, D, Howley, P, Griffin, D, Lamb, R, Martin, M, Roizman, B, and Straus, S, editors, Fields Virology, pages 1691–1740. Lippincott/The Williams & Wilkins Co., Philadelphia, PA, 5 edition, 2007.
[108] Wu, W, Booth, J, Duggan, E, Wu, S, Patel, K, et al. Innate immune response to H3N2 and H1N1 influenza virus infection in a human lung organ culture model. Virology, 396(2):178–188, 2010.
[109] Zamarin, D, Ortigoza, M, and Palese, P. Influenza A virus PB1-F2 protein contributes to viral pathogenesis in mice. J. Virol., 80(16):7976–7983, 2006.
[110] Zitzow, L, Rowe, T, Morken, T, Shieh, W, Zaki, S, et al. Pathogenesis of avian influenza A (H5N1) viruses in ferrets. J. Virol., 76(9):4420–4429, 2002.
Definitions
Viral Kinetics: The rate of change of virus as a function of the time postinfection.
Kinetic Model: A mathematical model, typically a set ordinary differential equations, that describes the viral kinetics.
R0: The basic reproductive ratio. Defined as the number of infected cells that are produced by a single infected cell at the initiation of infection.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
