Three-Factor Medication Problems
Objectives
After completing this chapter, you will successfully be able to:
Calculate three-factor–given quantity to one-factor–, two-factor–, or three-factor–wanted quantity medication problems involving a specific amount of medication or intravenous (IV) fluid based on the weight of the patient and the time required for safe administration.
Calculate problems requiring reconstitution or preparation of medications using information from a nursing drug reference, label, or package insert.
 Preventing Medication Errors
Preventing Medication ErrorsWhen medications are ordered for infants and children, the dosage of medication (g, mg, mcg, gr) based on the weight of the child must be considered as well as how much medication the child can receive per dose or day.
Although the physician or nurse practitioner orders the medications, the nurse must be aware of the safe dosage range for administration of medications. It is the responsibility of the nurse to check a nursing drug reference for the right dosage before administering a medication to a child to prevent medication errors.
When physicians or nurse practitioners order medications for critically ill patients, the patients must be closely monitored by the nurse for effectiveness of the medications. Often, the medications or intravenous (IV) fluids must be titrated for effectiveness, with an increase or decrease in the dosage based on the patient’s response.
Factors involved in the safe administration of medications or IV fluids for the critically ill patient include the dosage of medication based on the weight of the patient and the time required for administration. The medication may need reconstitution or preparation by the nurse for immediate administration in a critical situation. The weight of the patient also may need to be obtained daily to ensure accurate correlation with the dosage of medication ordered. A nursing drug reference provides the nurse with information related to dosage, weight, and time for safe administration of medication.
To be able to calculate three-factor–given quantity to one-factor–, two-factor–, or three-factor–wanted quantity medication problems, it is necessary to understand all of the components of the medication order and to be able to calculate medication problems in a critical situation. This chapter will teach you to calculate medication problems involving the dosage of medication based on the weight of the patient and the time required for safe administration using dimensional analysis.
Three-factor–given quantity medication problems can be solved implementing the sequential method or the random method of dimensional analysis. The given quantity or the physician’s order now contains three parts, including a numerator (the dosage of medication ordered) and two denominators (the weight of the patient and the time required for safe administration).
Below is an example of this problem-solving method showing placement of basic dimensional analysis terms applied to a three-factor medication problem.
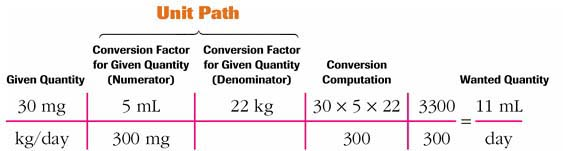 |
Example 6.1
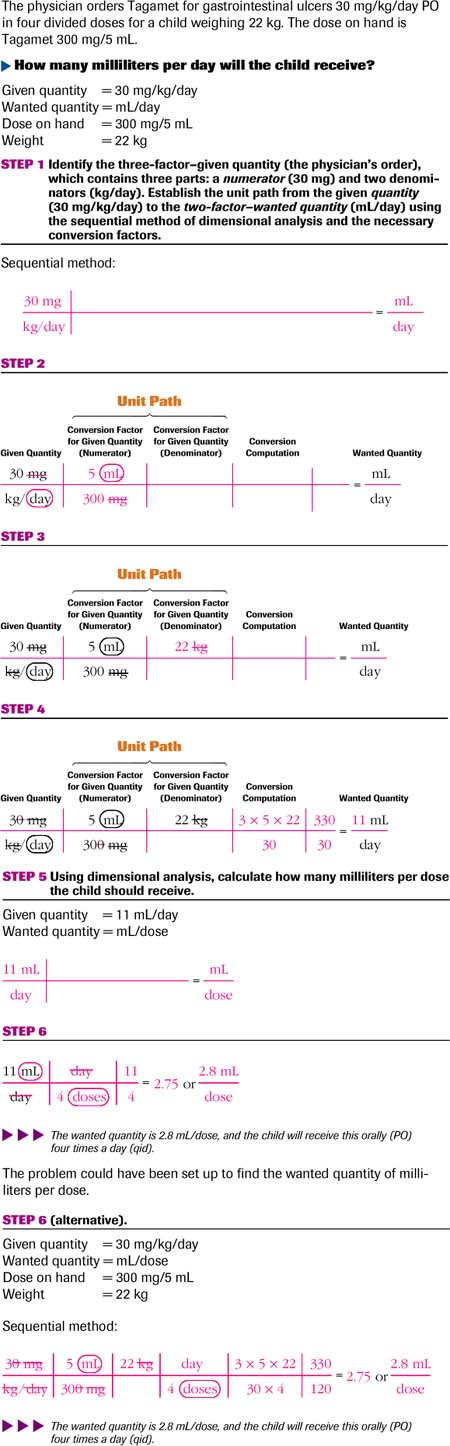
The physician orders Tagamet for gastrointestinal ulcers 30 mg/kg/day PO in four divided doses for a child weighing 22 kg. The dose on hand is Tagamet 300 mg/5 mL.
 Thinking it Through
Thinking it Through The three-factor–given quantity has been set up with a numerator (30 mg) and two denominators (kg/day) leading across the unit path to a two-factor–wanted quantity, with a numerator (mL) and a denominator (day). The conversion factors can now be factored into the unit path to allow cancellation of unwanted units.
The three-factor–given quantity has been set up with a numerator (30 mg) and two denominators (kg/day) leading across the unit path to a two-factor–wanted quantity, with a numerator (mL) and a denominator (day). The conversion factors can now be factored into the unit path to allow cancellation of unwanted units.The dose on hand (300 mg/5 mL) has been factored in and placed so that the wanted unit (mL) correlates with the wanted quantity (mL) and the unwanted unit (mg) is canceled.
The child’s weight (22 kg) has been factored in and set up to allow the unwanted unit (kg) to be canceled.
All the unwanted units have been canceled, and the wanted units are placed to correlate with the two-factor–wanted quantity (mL/day). Multiply numerators, multiply denominators, and divide the product of the numerators by the product of the denominators to provide the numerical answer. The wanted quantity is 11 mL/day.
The child is to receive 11 mL/day in four divided doses; therefore, the conversion factor involves how many doses are in a day (4 divided doses = day).
 |
 Preventing Medication Errors
Preventing Medication ErrorsEvery new medication order for a child should be carefully reviewed for errors related to dosage, route, and frequency. Many medication errors can be eliminated if a double-check system is in place for all new medication orders.
Example 6.2
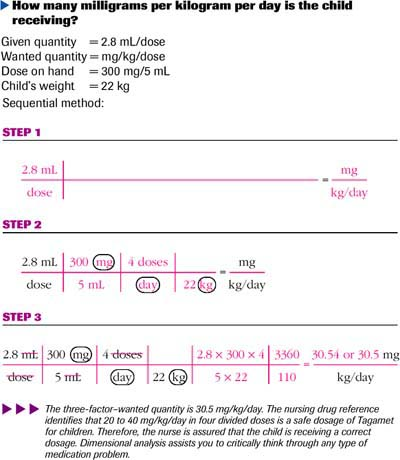
As a prudent nurse, you are concerned that the child may be receiving an unsafe dosage of Tagamet; therefore, you want to identify how many milligrams per kilogram per day (mg/kg/day) the child weighing 22 kg is receiving. The dosage of medication being given four times a day is 2.8 mL/dose. The dosage on hand is 300 mg/5 mL.
 |
 Thinking it Through
Thinking it Through The two-factor–given quantity (2.8 mL/dose) has been factored in with a numerator (2.8 mL) and a denominator (dose). The three-factor– wanted quantity (mg/kg/day) also has been factored in with a numerator (mg) and two denominators (kg/day).
The two-factor–given quantity (2.8 mL/dose) has been factored in with a numerator (2.8 mL) and a denominator (dose). The three-factor– wanted quantity (mg/kg/day) also has been factored in with a numerator (mg) and two denominators (kg/day).The conversion factors have been added, and all unwanted units have been canceled from the problem. The wanted unit (mg) is placed in the numerator to correlate with the wanted quantity (mg) also in the nu- merator. The wanted units (kg and day) are in the denominator to correlate with the wanted quantity (kg and day) in the denominator.
 Preventing Medication Errors
Preventing Medication ErrorsKnowing the Six Rights of medication administration can help to eliminate medication errors but another important consideration is being aware of the safe dosage range for each medication being administered.
A Nursing Drug Reference lists the safe dosage range for adults, children, and infants. It is the responsibility of the nurse to be familiar with safe dosage ranges to prevent medication errors.
Example 6.3
The physician orders dobutamine 5 mcg/kg/min IV for cardiac failure. The pharmacy sends an IV bag labeled: dobutamine 250 mg/50 mL D5W/0.45% NS. The patient weighs 165 lb.
 Thinking it Through
Thinking it ThroughThe three-factor–given quantity has been set up with a numerator (5 mg) and two denominators (kg/min) leading across the unit path to a two-factor–wanted quantity with a numerator (mL) and a denominator (hr). By using the random method of dimensional analysis, the conversion factors are factored to cancel out unwanted units.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


