Solving Problems Using Dimensional Analysis
Objectives
After completing this chapter, you will successfully be able to:
Define the terms used in dimensional analysis.
Explain the step-by-step problem-solving method of dimensional analysis.
Solve problems involving common equivalents using dimensional analysis as a problem-solving method.
 Preventing Medication Errors
Preventing Medication ErrorsDimensional analysis provides a systematic, straightforward way to set up problems and to organize and evaluate data. It is not only easy to learn, but also can reduce medication errors when mathematical conversion is required.
Dimensional analysis assists with preventing medication errors by allowing you to visualize all parts of the medication problem and to critically think your way through the problem.
This chapter introduces you to dimensional analysis with a step-by-step explanation of this problem-solving method. The chapter also provides the opportunity to practice solving problems that involve common equivalents.
Terms Used in Dimensional Analysis
Dimensional analysis is a problem-solving method that can be used whenever two quantities are directly proportional to each other and one quantity must be converted to the other by using a common equivalent, conversion factor, or conversion relation. All medication dosage calculation problems can be solved by dimensional analysis.
It is important to understand the following four terms that provide the basis for dimensional analysis.
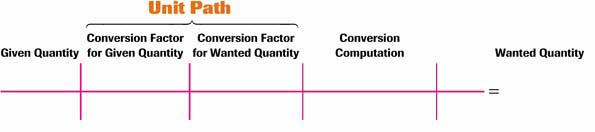
Given quantity: the beginning point of the problem
Wanted quantity: the answer to the problem
Unit path: the series of conversions necessary to achieve the answer to the problem
Conversion factors: equivalents necessary to convert between systems of measurement and to allow unwanted units to be canceled from the problem
Each conversion factor is a ratio of units that equals 1.
Dimensional analysis also uses the same terms as fractions: numerators and denominators.
Numerator = the top portion of the problem
Denominator = the bottom portion of the problem
Some problems will have a given quantity and a wanted quantity that contain only numerators. Other problems will have a given quantity and a wanted quantity that contain both a numerator and a denominator. This chapter contains only problems with numerators as the given quantity and the wanted quantity.
Once the beginning point in the problem is identified, then a series of conversions necessary to achieve the answer is established that leads to the problem’s solution.
Below is an example of the model that is used in solving problems by the dimensional analysis method. It also demonstrates the correct placement of the basic terms that are used in this method.
 |
The Five Steps of Dimensional Analysis
Once the given quantity is identified, the unit path leading to the wanted quantity is established. The problem-solving method of dimensional analysis uses the following five steps.
Identify the given quantity in the problem.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


