Phase III trials are typically undertaken after Phase II studies have identified a potentially safe and effective dose that is considered likely to show an effect on a relevant clinical end point. Typically, regulatory approval in the United States requires two statistically significant, well-controlled clinical trials for the same indication.

Phase III trials usually enroll several hundred to several thousand subjects at multiple study centers. The major objective in Phase III is to show a statistically significant effect on the relevant efficacy measure to facilitate approval of the drug by regulatory agencies, confirming evidence collected in Phase II that a drug is safe and effective for use in the intended indication and population. Secondary objectives can include evaluating safety and dosing for package labeling; its use in subpopulations, wider populations, and with other medications; and effects on secondary end points (1) (Table 8–1).

Phase III trials show efficacy by comparing the new therapy to a control, which can be standard therapy, no therapy, or a placebo. The most frequently used trial design is the superiority trial, which aims to show that the new therapy is better than the comparator. When effective treatments for a condition are already available, however, showing superiority against these treatments can be much more difficult than showing it against a placebo. In some cases, such large numbers of patients would be needed to declare superiority that performing such a trial becomes prohibitive. It may be more reasonable to show that the new therapy is equivalent or noninferior to existing standard therapy with regard to efficacy and safety while also showing other characteristics that make it desirable, for example, fewer side effects, shorter half-life, easier to give, or less expensive. The goal of an equivalence trial is to show that the effects of the new therapy differ by no more than a clinically acceptable amount from those of the comparative therapy, whereas the goal of a noninferiority trial is to show that any difference in effectiveness between the new therapy and the control is not worse by a clinically meaningful amount.

Phase III trials are frequently designed to include specified interim “looks” at the data by an independent committee composed of knowledgeable experts, often referred to as a Data and Safety Monitoring Board (DSMB). This committee assesses the available trial data to determine whether there is sufficient cause for stopping the trial early or modifying trial conduct. Reasons for early stopping include a clear indication that the treatment is superior, a low likelihood of achieving the specified treatment benefit, unacceptable adverse events, and patient accrual that is too slow to complete the study in a timely manner. During an interim look, numerous quantitative methods can be used to evaluate the data for a clear indication that the treatment is superior. The most widely accepted methods used in current clinical trials are frequentist procedures, such as group-sequential boundaries. With these methods, critical values for hypothesis-testing are set for each evaluation of the end point such that the overall Type I error criteria will be satisfied and thus the Type I error rate will be controlled. Clinical trials are also terminated if there is little chance, given the currently available data, that a treatment will be beneficial. Conditional power and predictive power are two methods available for assessing the futility of continuing the trial. Regardless of the methods used to evaluate interim data, interpreting the data and making decisions about early stopping are difficult and often error-prone. Although quantitative methods of evaluation are important, it is critical to have a knowledgeable and experienced DSMB evaluate all aspects of the trial and make decisions based on all information available to them and not on statistical tests alone.

The most widely used treatment-allocation method in a clinical trial is randomization. Randomization is an effective way to reduce selection bias because a patient’s treatment assignment is based on chance. A simple randomization assigns treatment to a patient without regard for treatment assignments already made for other patients. This type of randomization can cause undesirable effects in a clinical trial, such as an imbalance in the number of patients in each treatment group or an imbalance among important prognostic factors. Although statistical methods are available to account for imbalances, large differences in important prognostic factors between treatment groups can raise credibility issues.

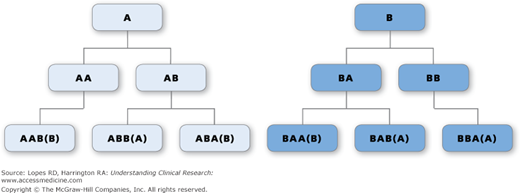
To prevent these imbalances, blocking is often used in randomization schemes. A block is a number of treatment assignments specified in advance, with the block size being an integer multiple of the number of treatment groups. The order of treatments within a block is randomly permuted, but the number of each treatment is balanced within each block. For example, in a block size of four, one can have the following six blocks: AABB, ABAB, ABBA, BBAA, BABA, and BAAB. A block is picked at random, and that block defines the first set of treatment assignments (Figure 8-1). For this design of a block size of four, the most that the treatment allocations could differ within any one center is by two.

All blocks do not need to be the same size. As illustrated in Figure 8-1, if investigators can determine the treatments that patients receive (or think they can), then once the first three treatments in a block are given, the assignment to the fourth patient would be known. This could influence the investigator’s decision to enroll a particular patient to receive that fourth assignment. To control for this, a random block design may be used. In this case, blocks that are multiples of the number of treatments are developed. For our two-treatment study, these could be block sizes of two, four, six, etc. Treatment allocation within large Phase III trials is often blocked within each center, resulting in a nearly balanced number of patients in each treatment group at each center.

Other types of treatment allocation include dynamic or adaptive allocation methods. Minimization and biased coin are two types of such methods. Minimization tries to balance treatment allocation across important prognostic factors. This method uses the levels of the stratification factors of the patients already in the trial, the treatment of each, and the values of these factors for the next patient in determining the treatment assignment for this next patient. An imbalance score is created for the patient for each treatment assignment, and the treatment with the smallest score is assigned. For the biased coin, a patient is randomly allocated to the treatment arm with fewer patients with a probability P > 0.5. In the adaptive biased coin design, the value of P depends on the level of imbalance in the number of patients already allocated to each arm.

When evaluating efficacy outcomes, the principle of intention to treat (ITT) is generally applied. According to the ITT principle, the statistical analysis includes patients in the treatment group to which they were assigned through randomization. Thus, patients who die or withdraw before being treated, receive the wrong treatment, or switch from one treatment group to another during the study are still considered, for the main efficacy analyses, to have received the therapy to which they were randomized. This method preserves the assumption of random allocation of therapy. It also reduces potential bias that could result from selecting patients to preferentially receive one treatment or another.

In some trials there may be reasonable cause to eliminate one or more patients from the ITT analysis (e.g., there may be patients randomized who do not meet entry criteria, patients not exposed to study treatment, or patients lost to follow-up.) Analysis of a modified ITT (MITT) population excluding these patients may still be in accordance with ITT principles, provided that the mechanism for excluding patients is not associated with treatment assignment. To avoid concerns about potential inflation of Type I error, it is best to describe the plan for any MITT analyses in the protocol. A large number of unanticipated exclusions from the ITT could raise concerns about the conduct of a trial.

To acquire a comprehensive safety profile for new therapies, safety outcomes are typically analyzed according to treatment received and not randomized treatment. Patients are assessed for routine safety endpoints from the time they are first exposed to study treatment until a specified time point after their last exposure to the treatment—e.g., 30 days or 60 days. Serious and unexpected adverse events occurring after the end of planned follow-up are generally reported to the license holder of the study treatment and the appropriate regulatory authorities.

The amount of missing data has a substantial effect on the overall quality of clinical trials (2). The problem can be especially severe with longer trials and those with incomplete ascertainment of fatal and nonfatal end points. For this reason, it is usually important to make a clear distinction in the protocol between nonadherence (i.e., not receiving a randomized intervention) and nonretention (i.e., not ascertaining the end point of interest). The occurrence of side effects, inability to tolerate the intervention, toxicity, or need for other therapies can be valid reasons for nonadherence, but not for nonretention. Ideally, the only valid reason for nonretention is the withdrawal of consent. Nonretention rates of >1% could bring into question the study results.

Phase III Studies of Eptifibatide